Patch-match binocular 3D reconstruction based on deep learning
-
摘要:
以patch-match为核心的算法在双目立体重建中有着广泛应用,因其具有低内存消耗、重建精度高等优良性能;然而,传统patch-match算法需要有序地对图像中的每一个像素点进行迭代求取最优视差值d,从而导致运行时间较高。为了解决该问题,在传统patch-match算法的基础上引入基于学习的模型作为指导来降低运行时间,提高立体重建精度。利用深度学习模型输出每个像素伴有异方差不确定度的初始视差图,异方差不确定度用于衡量网络模型所预测视差值的准确度;将异方差不确定度和初始视差作为patch-match算法的先验信息;在平面细化步骤中,利用每个像素点的异方差不确定度大小动态调整其搜索区间,实现减少运行时间的目标。在Middlebury数据集上,通过与原有算法比较可知,改进后的算法在运行时间上减少20%,同时,在不连续等区域上的重建精度得到略微提高。
Abstract:The patch-match algorithm has been widely used in binocular stereo reconstruction due to its low memory consumption and high reconstruction accuracy. However, the traditional patch-match algorithm needs to iteratively calculate the optimal disparity d for each pixel of image in an orderly manner, which resulting in a high running time. In order to solve this problem, a learning-based model on the basis of traditional patch-match algorithm as a guide to reduce the running time and improve the accuracy of stereo reconstruction was introduced. First, the deep learning model was used to output the initial disparity map of each pixel with heteroscedastic uncertainty, which was used to measure the accuracy of the disparity predicted by the network model. Then, the heteroscedastic uncertainty and initial disparity were taken as the prior information of patch-match algorithm. Finally, in the plane refinement step, the heteroscedastic uncertainty of each pixel was used to dynamically adjust its search interval to achieve the goal of reducing the running time. On the Middlebury dataset, compared with the original algorithm, the running time of the improved algorithm is reduced by 20%, and the reconstruction accuracy of the discontinuous region is slightly improved.
-
Keywords:
- 3D reconstruction /
- deep learning /
- heteroscedastic uncertainty /
- precision
-
引言
双目立体视觉在机器人导航、AR/VR、室内场景三维重建中有广泛应用。其中,patch-match[1]算法以内存消耗低、重建精度高的性能被很多研究者所采用[2-4]。然而,patch-match[1]算法在求取视差$d$时,需要有序地对视图中的每个像素进行随机初始化和迭代求解,导致运行时间成本较高。针对上述问题,本文介绍对传统的patch-match[1]算法的优化方法。
卷积神经网络在计算机视觉中的很多领域都取得了很好的效果,例如:目标检测和识别[5-6]、语义分割[7-8]等。上述成果带给人们解决传统算法在重建不连续等区域所面临难题的希望。在一些复杂多变的户外环境中,基于深度学习的算法[9-11]进行立体视觉重建时的精度要优于传统算法,同时,其时间复杂度相对较低。文献[12-13]中,作者利用卷积神经网络寻找对应点,例如在MC-CNN (matching cost convolutional neural network)中,作者通过搭建一个孪生神经网络计算一对相同尺寸图像块的相似性得分,判断它们是否匹配。然而,MC-CNN[13]缺乏利用上下文信息,在容易出错的区域依然面临巨大挑战,例如反光、遮挡、不连续区域等。为了让网络模型充分利用图像的上下文信息,在GC-net (geometry and context network)[11]和PSM-net (pyramid stereo matching network)[14]中,作者通过搭建一个端到端的编码-解码网络结构和金字塔池化去融合不同尺度下的语义特征来扩大感受野范围,提高算法的鲁棒性和精度。基于学习的重建算法在比较复杂的环境中,具有传统算法不具备的优良性能。本文尝试将深度学习融入patch-match算法,使得patch-match算法继承深度学习的优良特性,并降低运行时间。
Patch-match算法求取每个像素的视差值$d$,需要经历5个阶段,即:随机初始化、空间传播、视角传播、时间传播和平面细化。其中,平面细化步骤消耗时间占据整个算法一半以上。因此本文主要目标之一是减少平面细化步骤的运行时间。在文献[1]中,作者对每个像素点视差进行平面细化,需要定义2个搜索区间$\Delta {\textit{z}}:\left[ { - \Delta _{{{\textit{z}}_0}}^{\max },\Delta _{{{\textit{z}}_0}}^{\max }} \right]$和$\Delta n = \left[ { - \Delta _n^{\max },\Delta _n^{\max }} \right]$进行迭代搜索。我们发现准确度高的视差值$d$不需要很大的搜索空间。为此我们考虑了针对每个像素进行动态调整$\Delta _{{{\textit{z}}_0}}^{\max }$和$\Delta _n^{\max }$的方法。
研究[15]发现深度学习模型预测视差,可以有效地评估预测视差$d$的准确度。在文献[16]中,Yaoyu Hu基于改造的PSM-net[14]网络预测每个像素初始的视差值$d$和对应的异方差不确定度$\sigma $,利用$\sigma $缩小SGBM[17]视差匹配区间范围。出于相同目的,我们搭建了一个可以同时输出深度图和异方差不确定度的深度学习模型,$\sigma $越大表示网络输出的视差$d$越不稳定,在平面细化步骤中扩大它的搜索区间,如果$\sigma $很小,则相反。因此,我们根据每个像素$\sigma $的大小动态设置$\Delta _{{{\textit{z}}_0}}^{\max }$和$\Delta _n^{\max }$,降低平面细化步骤的运行时间,同时继承深度学习模型的优良性能。
1 算法原理
1.1 算法流程
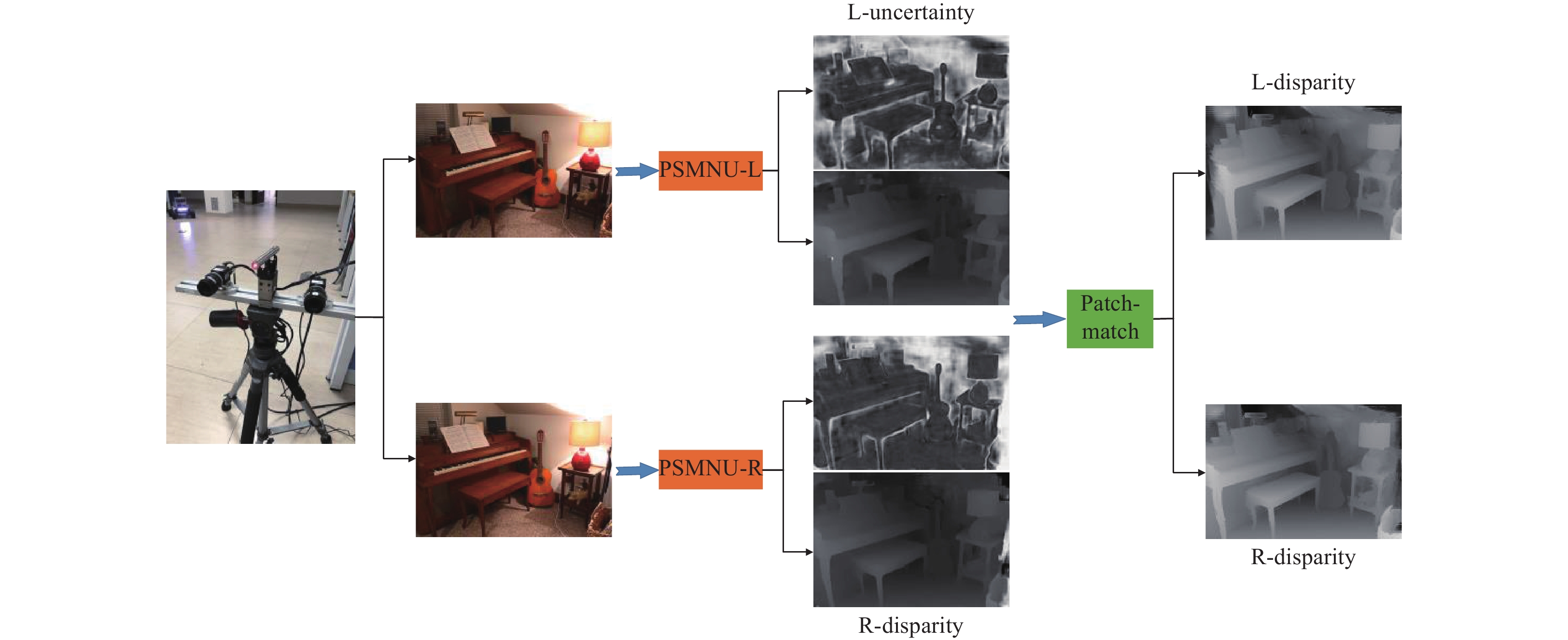
图1展示文中所提出算法的处理流程,首先,利用深度学习模型PSMNU(PSM-net with uncertainty)预测立体图片的左右视差图和异方差不确定度;然后,将视差$d$和异方差不确定度$\sigma $作为先验信息输入到patch-match算法中,在平面细化步骤中,利用异方差不确定$\sigma $动态设置$\Delta _{{{\textit{z}}_0}}^{\max }$和$\Delta _n^{\max }$;最后,修正后的patch-match算法输出最终的视差图。通过上述步骤,我们可以减少原始算法的运行时间,提高重建精度。
1.2 PSMNU网络
建立基于PSM-net[14]的PSMNU网络,如图2所示,该网络在预测稠密深度图方面具有良好性能。由于PSM-net[14]网络旨在输出深度图,为了同时输出异方差不确定度$\sigma $,根据文献[15]对PSM-net[14]的回归层进行修改,输出$H \times W \times D \times 2$维度的代价体积,H和W分别表示输入图像的高、宽,D表示最大视差。在代价体积中,最后维度(第4个维度)的第1个值表示每个像素在当前视差下的代价,第2个值表示异方差不确定度。
训练一个可以同时输出深度图和异方差不确定的深度网络,需要学习函数$f$来推断后验分布,$f$将一对立体输入图像${I_{\rm{L}}}$和${I_{\rm{R}}}$映射到视差估计$\hat d$和由方差给出的异方差不确定度量$\hat \sigma $,如(1)式:
$$ \left[ {\hat d,\hat \sigma } \right] = f\left( {{I_{\rm{L}}},{I_{\rm{R}}}} \right) $$ (1) 式中:$\hat d$和$\hat \sigma $分别是PSMNU输出的视差和异方差不确定度。为了保证PSMNU网络达到预期效果,设(2)式作为PSMNU网络的损失函数:
$$ L{\text{ = }}\frac{1}{{2{N_p}}}\sum\limits_{p \in p} {{E_p}{e^{ - {\sigma _p}}}} + \frac{1}{{2{N_P}}}\sum\limits_P {{\sigma _P}} $$ (2) 式中:$N{}_p$表示图像中的像素数量;${E_p}$和${\sigma _p}$分别定义如(3)式和(4)式。(2)式中的损失函数由2部分组成:残差回归和一个不确定性正则项。实验中,我们不需要“异方差不确定性标签”来学习异方差不确定性,相反,只需要监督学习预测视差,就能从损失函数中隐式地学习异方差不确定$\sigma $。正则化的目的是防止网络对所有数据点预测无限大的$\sigma $,导致损失函数为零。同时,为了提高PSMNU网络的收敛性和稳定性,采用$smoot{h_{{L_1}}}$损失函数计算视差损失,由于其具有鲁棒性且对异常值不敏感[18]。
$$ {E_p} = smoot{h_{L_1}}(d{{ - }}\hat d) $$ (3) $$ smoot{h_{{L_1}}}(x) = \left\{ {\begin{array}{*{20}{c}} {0.5{x^2},}&{{\rm{if}}{\text{ }}\left| x \right| < 1} \\ {\left| x \right| - 0.5,}&{{\rm{otherwise}}} \end{array}} \right. $$ (4) 式中:$d$表示当前像素$p$的真实视差。
为了稳定计算和避免被零整除,迫使网络预测更精确的视差$\hat d$,我们设定:
$$ {\sigma _p} = {\hat \sigma ^2} $$ (5) 小的$\hat \sigma $意味着网络对输出的视差$\hat d$具有更高的确信度。当$f$对$\hat d$不确定时,${E_P}$趋于变大,为了降低损失,PSMNU需要预测较大的$\hat \sigma $惩罚${E_P}$,(2)式中最后一项正则化会惩罚模型预测大的$\hat \sigma $,从而使$\hat \sigma $达到平衡。如果${E_P}$较小,则相反。
1.3 patch-match算法
Patch-match[1]是一个优秀的局部立体匹配算法,算法的处理流程如图3所示。
首先,输入一对矫正后的立体图片${m_{\rm{L}}}$和${m_{\rm{R}}}$;然后,通过随机初始化对${m_{\rm{L}}}$和${m_{\rm{R}}}$中的每一个像素随机分配一个视差值${{\textit{z}}_0}$和单位向量${\boldsymbol{n}} = ({n_x},{n_y},{n_{\textit{z}}})$;最后,对左右视差图分别进行迭代优化。迭代步骤包括4个阶段:1) 空间传播,将位于$p$邻域内的像素$q$的平面${f_q}$给予$p$,如果$m(p,{f_q}) < m(p,{f_p})$,则接受${f_q}$作为$p$的新平面;2) 视图传播,将位于$p$第2个视角中的对应像素$p'$的平面${f_{p'}}$给予$p$,如果$m(p,{f_{p'}}) < m(p,{f_p})$,则接受${f_{p'}}$作为$p$的新平面;3) 时间传播,这种形式的传播只适合处理视频序列立体重建,将上一帧像素的${f_{p'}}$给予当前帧相同位置$p$,如果$m(p,{f_p}^\prime ) < m(p,{f_p})$,则接受${f_p}^\prime $作为$p$的新平面;4) 平面细化:不断更新${{\textit{z}}_0}$和${\boldsymbol{n}} = ({n_x},{n_y},{n_{\textit{z}}})$,从而获取一个新平面${f_p}^\prime $,如果$m(p,{f_p}^\prime ) < m(p,{f_p})$,则接受${f_p}^\prime $作为$p$的新平面。根据平面f计算匹配像素p的聚合代价,如(6)~(8)式:
$$ m(p,f) = \sum\limits_{q \in {W_p}} {w\left( {p,q} \right) \cdot \rho (q,q - ({a_f}{q_x} + {b_f}{q_y} + {c_f}} )) $$ (6) $$ w(p,q) = {e^{ - \frac{{\left\| {{I_P} - {I_q}} \right\|}}{\gamma }}} $$ (7) $$\begin{split} \rho \left( {q,q'} \right) = \;&\left( {1 - \partial } \right) \cdot \min \left( {\left\| {{I_P} - {I_{q'}}} \right\|,{\tau _{{\rm{col}}}}} \right) +\\ &\partial \cdot \min \left( {\left\| {\nabla {I_q} - \nabla {I_{q'}}} \right\|,{\tau _{{\rm{grad}}}}} \right) \end{split} $$ (8) 式中:${W_P}$表示以像素$p$为中心的方形窗口;${a_f}$、${b_f}$、${c_f}$表示位于像素${q_{}}$处的平面参数;${q_x}$、${q_y}$分别表示像素${q_{}}$在图像坐标系中的水平坐标和竖直坐标;权重函数$w(p,q)$利用颜色相似性判断p与q位于相同平面的可能性;${I_p}$、${I_q}$分别表示像素$p$、${q_{}}$的灰度强度;函数$\rho (q,q')$用于计算像素p、$q'$之间的不相似性;$\partial $、${\tau _{{\rm{col}}}}$、${\tau _{{\rm{grad}}}}$是超参数,具体细节可参考文献[1]。
1.4 修正patch-match
在文献[1]中,作者利用像素点坐标、法向量表示${f_p}$。首先,分别定义2个参数,$\Delta _{{{\textit{z}}_0}}^{\max }$表示3D点中z坐标所允许的最大变化范围,即:$\Delta _n^{\max }$表示法向量${\boldsymbol{n}}$所允许的最大变化范围。作者在区间$\left[ {{{ - }}\Delta _{{{\textit{z}}_0}}^{\max },\Delta _{{{\textit{z}}_0}}^{\max }} \right]$中随机估计$\Delta {{\textit{z}}_0}$并计算${{\textit{z}}'_0} = {{\textit{z}}_0} + {\Delta _{{{\textit{z}}_0}}}$,从而获取一个新的3D点 $P' = (x,y,{{\textit{z}}'_0})$。类似的,在区间$\left[ {{{ - }}\Delta _n^{\max },\Delta _n^{\max }} \right]$估计3个随机值用于形成向量${ {\boldsymbol{\Delta _n}}}$,然后计算修正后的法向量${\boldsymbol{n}}' = {{u}}\left( { {\boldsymbol{n}} + {{ {\boldsymbol{\Delta }_{\boldsymbol{n}}}}}} \right)$,其中$u\left( {} \right)$用于计算单位向量。最终,用更新后的参数$P'$和${{\boldsymbol{n}}'}$去修正位于当前像素点$p$上的平面${f_p}$,再通过(9)式求出当前视差${d_p}$。如果$m(p,{f'_p}) < m(p,{f_p})$,我们就接受该平面 。
$$ {d_p} = {a_{{f_p}}}{p_x} + {b_{{f_p}}}{p_y} + {c_{{f_p}}} $$ (9) 每一次更新视差、法线,需要再次代价聚合,导致patch-match的运行时间主要集中在平面细化阶段[1]。为了降低patch-match的运行时间,需对平面细化阶段进行优化。
在上述步骤中,我们通过PSMNU网络获得左右视图的视差$\hat d$和异方差不确定度$\sigma $,并将$\hat d$和$\sigma $作为patch-match的先验信息。在随机初始化步骤中,用$\hat d$初始化每一个像素视差,保证绝大数像素的初始视差有良好的初始值。因此,在平面细化阶段,不需要对所有像素进行大范围搜索。利用$\sigma $获取PSMNU对预测视差$\hat d$的确信程度,对于低$\sigma $的像素,可以缩小$\Delta _{{{\textit{z}}_0}}^{\max }$和$\Delta _n^{\max }$的区间范围,降低平面细化的迭代次数。如果$\sigma $很大,则保持$\Delta _{{{\textit{z}}_0}}^{\max }$和$\Delta _n^{\max }$的区间范围不变。通过上述步骤,不仅可以降低patch-match的运行时间,还会保证最优的视差值被找到。利用(10)~(13)式,可以确定每一个像素初始的$\Delta _{{{\textit{z}}_0}}^{\max }$和$\Delta _n^{\max }$。
$$ \Delta _{{{\textit{z}}_0}}^{\max } = \frac{{\max disp}}{{t \cdot {F_{{\sigma _e}}}\left( {{\sigma _e}} \right)}} $$ (10) $$ \Delta _n^{\max } = \frac{1}{{t \cdot k \cdot {F_{_{{\sigma _e}}}}\left( {{\sigma _e}} \right)}} $$ (11) $$ {F_{{\sigma _e}}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {16},&{{\rm{if}}{\text{ }}{\sigma _e} = 1} \\ 4,&{{\rm{if}}{\text{ }}{\sigma _e} > 1{\text{ }}{\rm{and}}{\text{ }}{\sigma _e} < = 10} \\ 2,&{{\rm{otherwise}}} \end{array}} \right. $$ (12) $$ {\sigma _e} = {e^{\sigma _p^2}} $$ (13) 式中:$t$表示当前第几次迭代;$k$是一个超参数,对于所有的实验设置$k = 0.5$。
2 分析与讨论
所有实验均在一台拥有2.90 GHz Intel Core i5-9400F CPU和8 GB RAM的PC机上的Visual Studio 2017中进行,软件环境为Windows 64位操作系统,编程语言是C++,需要的第三方库为OpenCV3.1.0。实验中,总共需要2个数据库,分别是Scene Flow[18]和Middlebury Stereo Evaluation V3[19]。Scene Flow数据库主要用来训练PSMNU网络模型,Middlebury Stereo Evaluation V3用于验证文中算法的有效性。我们从PSMNU网络模型训练、实验结果比较两个方面来介绍实验部分,为了验证文中算法的有效性,对实验结果进行定性、定量分析。
2.1 PSMNU网络训练
本文PSMNU网络结构是基于PSM-net[14]实现,通过修改PSM-net中的损失函数、网络回归层、代价体积满足实验目的,具体实现细节可参考文献[15-16]。
实验中,使用PyTorch搭建PSMNU网络模型,所有模型都使用Adam$(\beta 1 = 0.9,\;\beta 2 = 0.999)$进行端到端优化。在训练过程中,对所有数据集进行颜色标准化及随机裁剪处理,保证图片尺寸满足256×512像素,设定最大视差D为192。使用Scene Flow[18]数据集在3个nNvidia 1080Ti GPUs上从头开始训练模型,学习速率为0.001,最小批次为9,每个显卡3个批次,连续训练10个批次需要17 h左右。最后,我们通过PSMNU-L和PSMNU-R对Scene Flow[18]数据集进行测试,如图4所示。图4(a)、图4(b)分别表示frames cleanpass的左右视图;图4(c)、图4(d)分别表示monkaa cleanpass的左右视图。预测视差$d$和$\sigma $均来自于PSMNU,为了更好地观看$\sigma $图,我们对异方差不确定度进行归一化操作。在物体的边缘处,如图片中的红色虚线圈区域,由于存在遮挡、视差的不连续性导致该处的$\sigma $会展示出很高的不确定性。
2.2 算法比较
为了比较文中算法与原始patch-match,我们采用文献[1]中的参数设置,用像素35×35的代价聚合窗口,同时设置相同参数$\left\{ {\gamma ,\partial ,{\tau _{{\rm{col}}}},{\tau _{{\rm{grad}}}}} \right\} = \left\{ {10,0.9,10,2} \right\}$,实验数据集均来自于Middlebury Stereo Evaluation V2[19]。图5展示文中算法与原始patch-match的实验结果。其中:图5(a)为Middlebury数据,从左到右依次为Tsukuba、Venus、Cones、Teddy;图5(b)为原始算法求取的深度图;图5(c)表示原始算法求取的视差值误差>1个像素(红色);图5(d)为PSMNU输出的深度图;图5(e) 为PSMNU输出的异方差不确定度;图5(f)为本文算法求取的深度图;图5(g)表示本文算法求取的视差值误差>1个像素(红色)。
从实验结果可以看出:本文算法在重建精度方面基本上与原始patch-match相同,为了定性地比较性能,用表1记录实验数据,所有数据重建精度的评价指标均使用Middlebury默认错误阈值1个像素。其中,Nonocc、Disc所在列的数据分别表示无遮挡区域中绝对视差错误大于1.0像素所占百分比、不连续区域中绝对视差错误大于1.0像素所占百分比。从时间栏可以看出,本文算法在效率方面明显优于原始算法patch-match,同时,重建精度略优于原始算法。本文算法性能的提高主要归结于PSMNU输出良好的视差图和异方差不确定度,输出的视差精度越高,越有助于本文算法确定一个较好的搜索起点。视差的精度与异方差不确定度成反比关系,在平面细化步骤中,小的$\sigma $意味着在小范围区间内就可以搜索到正确的视差。因此,PSMNU的鲁棒性影响着算法重建性能。与CSCA[20]算法进行比较时,本文算法的重建精度更胜一筹,但运行时间比较长。
表 1 Patch-match和本文算法的定量分析结果Table 1. Quantitative analysis results of patch-match algorithm and proposed algorithmDataSet Algorithm Thresh/
pixelNonocc/
%Disc/
%All/
%Time/
sTsukuba Patch-match[1] 1.0 4.21 10.56 4.44 286.795 Ours 1.0 4.16 10.46 4.43 221.337 CSCA[20] 1.0 5.03 10.02 5.80 0.24 Venus Patch-match[1] 1.0 1.53 9.44 2.12 458.980 Ours 1.0 1.40 8.64 1.94 383.256 CSCA[20] 1.0 1.49 8.53 2.28 0.41 Teddy Patch-match[1] 1.0 6.60 14.64 12.60 502.908 Ours 1.0 6.33 13.81 12.19 406.529 CSCA[20] 1.0 7.21 17.39 14.77 0.39 Cones Patch-match[1] 1.0 2.75 7.68 7.77 466.620 Ours 1.0 2.58 7.31 7.58 297.364 CSCA[20] 1.0 5.98 15.32 14.96 0.47 3 结论
传统的patch-match算法进行立体三维重建具有良好性能,然而需要较长的运行时间。本文引用深度学习模型,该模型可以输出初始视差值并评估视差预测的不确定性,我们利用评估得到的异方差不确定度动态调整每个像素的搜索区间,从而达到减少运行时间的目标。实验结果表明,本文提出的算法在效率和精度方面优于原始算法。未来期望该算法可以在GPU上运行,以达到实时性的目的;同时,让PSMNU结合多任务学习、多视角深度重建以提高鲁棒性。
-
表 1 Patch-match和本文算法的定量分析结果
Table 1 Quantitative analysis results of patch-match algorithm and proposed algorithm
DataSet Algorithm Thresh/
pixelNonocc/
%Disc/
%All/
%Time/
sTsukuba Patch-match[1] 1.0 4.21 10.56 4.44 286.795 Ours 1.0 4.16 10.46 4.43 221.337 CSCA[20] 1.0 5.03 10.02 5.80 0.24 Venus Patch-match[1] 1.0 1.53 9.44 2.12 458.980 Ours 1.0 1.40 8.64 1.94 383.256 CSCA[20] 1.0 1.49 8.53 2.28 0.41 Teddy Patch-match[1] 1.0 6.60 14.64 12.60 502.908 Ours 1.0 6.33 13.81 12.19 406.529 CSCA[20] 1.0 7.21 17.39 14.77 0.39 Cones Patch-match[1] 1.0 2.75 7.68 7.77 466.620 Ours 1.0 2.58 7.31 7.58 297.364 CSCA[20] 1.0 5.98 15.32 14.96 0.47 -
[1] BLEYER M, RHEMANN C, ROTHER C. PatchMatch stereo-stereo matching with slanted support windows[C]//British Machine Vision Conference 2011. Scotland: University of Dundee, 2011.
[2] XU H, CHEN X, LIANG H, et al. CrossPatch-based rolling label expansion for dense stereo matching[J]. IEEE Access,2020,8:63470-63481. doi: 10.1109/ACCESS.2020.2985106
[3] BARNES C, SHECHTMAN E, FINKELSTEIN A, et al. PatchMatch: a randomized correspondence algorithm for structural image editing[J]. ACM Transactions on Graphics,2009,28(3):1-24.
[4] BARNES C, SHECHTMAN E, DAN B G, et al. The generalized PatchMatch correspondence algorithm[C]//European Conference on Computer Vision, Heraklion, Greece, September 5-11, 2010. Berlin: Springer, 2010: 29-43.
[5] 马少斌, 张成文. 基于双路多尺度金字塔池化模型的显著目标检测算法[J]. 应用光学,2021,42(6):1056-1061. doi: 10.5768/JAO202142.0602007 MA Shaobin, ZHANG Chenwen. Salient target detection algorithm based on dual-channel multi-scale pyramid pooling model[J]. Journal of Applied Optics,2021,42(6):1056-1061. doi: 10.5768/JAO202142.0602007
[6] GIRSHICK R, DONAHUE J, et al. Rich feature hierarchies for accurate object detection and semantic segmentation[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, June 23-28, 2014. USA: IEEE, 2014: 580-587.
[7] 曹富强, 王明泉, 张俊生, 等. 基于深度学习的铸件X射线图像分割研究[J]. 应用光学,2021,42(6):1025-1033. doi: 10.5768/JAO202142.0602003 CAO Fuqiang, WANG Mingquan, ZHANG Junsheng, et al. Research on X-ray image segmentation of castings based on deep learning[J]. Journal of Applied Optics,2021,42(6):1025-1033. doi: 10.5768/JAO202142.0602003
[8] RONNEBERGER O, FISCHER P, BROX T. U-Net: convolutional networks for biomedical image segmentation[C]// 18th International Conference on Medical Image Computing and Computer-Assisted Intervention.Berlin:Springer,2015: 234-241.
[9] SEKI A, POLLEFEYS M. SGM-Nets: semi-global matching with neural networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition , Honolulu, HI, July 21-26, 2017. USA: IEEE, 2017: 6640-6649.
[10] WU S, RUPPRECHT C, VEDALDI A. Unsupervised learning of probably symmetric deformable 3D objects from images in the wild[C]// 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition , Seattle, WA, June 13-19, 2020. USA. : IEEE, 2020: 1-10.
[11] KENDALL A, MARTIROSYAN H, et al. End-to-end learning of geometry and context for deep stereo regression[C]//2017 IEEE International Conference on Computer Vision , Venice, Italy, October 22-29, 2017. USA: IEEE, 2017: 66-75.
[12] BONTAR J, LECUN Y. Computing the stereo matching cost with a convolutional neural network[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition , Boston, MA, June 7-12, 2015. USA. IEEE, 2015: 1592-1599.
[13] ŽBONTAR J, LECUN Y. Stereo matching by training a convolutional neural network to compare image patches[J]. The Journal of Machine Learning Research,2016,17(1):2287-2318.
[14] CHANG J R, CHEN Y S. Pyramid stereo matching network[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition , Salt Lake City, UT, June 18-23, 2018. USA. IEEE, 2018: 5410-5418.
[15] KENDALL A G . Geometry and uncertainty in deep learning for computer vision[D]. London: University of Cambridge, 2019.
[16] HU Yaoyu, ZHEN Weikun, et al. Deep-learning assisted high-resolution binocular stereo depth reconstruction[C]//2020 IEEE International Conference on Robotics and Automation , Paris, France, May 31-August 31, 2020. USA: IEEE, 2020: 8637-8643.
[17] HIRSCHMULLER H. Stereo processing by semiglobal matching and mutual information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 30(2): 328 – 341.
[18] MAYER N, ILG E, et al. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition , Las Vegas, NV, June 27-30, 2016. USA: IEEE, 2016: 4040-4048.
[19] SCHARSTEIN D, HIRSCHMÜLLER H, KITAJIMA Y, et al. High-resolution stereo datasets with subpixel-accurate ground truth[C]// 36th German Conference on Pattern Recognition, 2014, 8753: 31-42.
[20] ZHANG Kang, FANG Yuqiang, et al. Cross-scale cost aggregation for stereo matching[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, June 23-28, 2014. USA, IEEE, 2014: 1590-1597
-
期刊类型引用(6)
1. 杨力. 基于双目视觉的三维场景图像表面重建算法. 现代电子技术. 2024(04): 71-75 .  百度学术
百度学术
2. 白维维,李俊杰,陈烽. 基于双目图像深度学习的农作物择优采摘仿真. 计算机仿真. 2024(02): 187-191 .  百度学术
百度学术
3. 孙同明,任俊,张峰,廖春云. 基于逆向工程的航空发动机叶片三维重建模型构建. 计算机测量与控制. 2024(09): 249-255 .  百度学术
百度学术
4. 韦玮,陈芬,张华波,罗英国,张鹏,彭宗举. 基于亚像素和梯度引导的光场图像超分辨率. 应用光学. 2024(05): 956-965 .  本站查看
本站查看
5. 张子康,殷松峰,曹良才,刘成. 基于身份-年龄共享特征的跨年龄人脸识别方法. 应用光学. 2023(03): 565-570 .  本站查看
本站查看
6. 宁孟丽,樊亚栋. 仿真技术在我国旅游领域应用现状的研究. 计算机仿真. 2023(08): 264-269 .  百度学术
百度学术
其他类型引用(2)



 下载:
下载:




 陕公网安备 61011302001501号
陕公网安备 61011302001501号 