In situ detection and evaluation of surface defects for large-aperture optical elements
-
摘要: 精密光学元件在加工过程中如果工艺控制不当,产生的划痕、麻点等疵病分布范围虽然较小,但对整个光学系统的性能影响却很大,破坏力非常强,目前的表面疵病检测仪基本上针对平面或球面光学元件进行离线检测。文章以光学加工机床为运动平台,采用暗场散射成像方法,设计多光束均匀照明系统,研究表面疵病微细特征的识别算法,实现大口径光学表面疵病的在位检测与评价;标定结果表明,表面疵病宽度偏差为2.05%,长度偏差为2.39%,满足指标要求;在此基础上针对Φ280 mm平面硅镜进行自动化在位检测,给出了不同类型疵病的统计数据,解决了离线检测中非加工时间长与多次装夹引起定位误差等问题。Abstract: If the technology is not properly controlled in the machining process of precision optical elements, although the distribution range of defects such as scratch and pitting is small, it has great influence on the performance of optical system and is very destructive. At present, the surface defect detectors are mainly used for off-line detection of planar or spherical optical elements. The optical machine tool was used as the motion platform, the method of scattering imaging was adopted in dark field, the uniform illumination system with multi-beam was designed, the recognition algorithms of fine features on surface defects were studied, and in-situ detection and evaluation of surface defects for large-aperture optical elements were achieved. Calibration results show that the width deviation of surface defect is 2.05% and the length deviation is 2.39%, which meet the index requirement. On this basis, automated in situdetection is carried out for Φ280 mm planar silicon mirror. The statistical data of different defects is given, and the problems of long non-machining time and locating error caused by multiple clamping in off-line detectionare solved.
-
Keywords:
- optical elements /
- surface defects /
- scattering imaging /
- In situ detection /
- image processing
-
引言
1948年,美国电信工程师H.奈奎斯特在信号学研究领域提出奈奎斯特采样定律。21世纪初,华人数学家陶哲轩在图像信号复原研究中意外发现了一种现象,采样频率即使没有达到奈奎斯特采样定律的要求,也能够完美地还原重构出原始信号。因此,陶哲轩等人于2006年提出压缩感知(compressive sencing)采样理论。利用信号的稀疏特性,在远小于奈奎斯特采样率的条件下,用随机采样获取信号的离散样本,最终通过重建算法重建信号。压缩感知理论提出后,在信息、图像、生物、光学、计算机等领域获得了广泛应用[1]。
超快成像是一种用于捕捉超快过程的图像成像技术,它能够实时观察和记录ns至fs级别的快速动态场景。它的发展最早起源于超快激光技术的出现,在20世纪80年代,高能量高功率激光的发展使得研究人员开始关注超快动态过程的实时观测。随着激光技术的广泛普及和发展,超快成像领域愈发需要快速且灵敏的成像探测器[2]。条纹变像管是超快成像领域的主流设备之一,它具有ps量级的高时间分辨能力,常用于惯性约束聚变(inertial confinement fusion, ICF)超快诊断。将压缩感知技术引入到条纹变像管,条纹相机将获得更多用武之地[3]。如光学领域中,观测飞秒脉冲激光实验,研究原子、分子、凝聚态物质的电子;材料学领域中,观测磁性材料自旋动力学的超快过程,探究材料的磁性行为;药学领域中,观测药物与受体吸收、分布和代谢的过程,研究药物的动力学和代谢动力学等。压缩感知与条纹相机结合的压缩超快成像系统可以在以上超快场景中发挥重要作用。
汪立宏院士团队于2014年提出了一种基于压缩超快成像技术的方法,设计了高效的数据采集和重建算法,解决了超快动态过程观测中的挑战[4]。他们的方法显著突破了传统超快诊断的成像速度,同时在图像质量方面也取得了优异的表现,进一步推动了压缩超快成像技术在超快领域的应用,为相关研究提供了有价值的参考。然而,目前的压缩超快成像技术仍面临一些挑战,例如在复杂场景或高噪声环境下的重建精度问题,以及更快的成像速度和更高的时间分辨率的要求。因此,本文针对这些问题展开研究,模拟了条纹相机的工作原理,利用还原算法重构信号,并与原始信号进行比较。模拟实验结果表明,压缩超快成像系统能以极高的时间分辨率准确记录皮秒激光的运动轨迹。
1 压缩超快成像系统模型
1.1 压缩感知理论
压缩感知理论中,待测信号的采样率远低于传统信号学中的奈奎斯特采样定律。压缩感知理论精确重建原始信号存在一定条件,原始信号必须满足稀疏表达,即对于N维的原始信号x(xϵRN),在某个确定的变换域中可以用较少的非零系数s(并且其他系数均为零或接近于零)以稀疏基Ψ(Ψ ϵ RN*N)来表示,如图1所示。x具有稀疏性,在变换域中是s-稀疏[5],即:
$$ x = \varPsi s $$ (1) 通常情况下,信号并非具有完美稀疏性。但是,只要信号近似满足稀疏性,即在某个变换域中大部份值均接近于零,且有小部分较大非零值,也可以认为该信号具有稀疏性,满足压缩感知算法采样还原基本条件。
确定稀疏域使信号满足稀疏性后,再构建与稀疏基Ψ具有非相关性的观测矩阵Ф。观测矩阵Ф的选取非常重要,其控制目标信号的采样,使信号从高维空间投射到低维空间,并保证目标信号有效信息在采样过程中不被丢失,且采用还原算法能够将压缩采样信号准确重构出原始信号[6],如图2所示。观测矩阵采样可表示为
$$ {\boldsymbol{y}}={\boldsymbol{\varPhi}} x={\boldsymbol{\varPhi}}\varPsi s $$ (2) 为了达到精准重构的效果,观测矩阵Ф需满足和稀疏基Ψ非相关性的特征,即约束等距准则(restricted isometry property, RIP)[7],RIP要求从观测矩阵中抽取的M个列向量构成的矩阵是非奇异的,ФΨ乘积设定为传感矩阵θ,合并矩阵如图3所示。
$$ {\boldsymbol{\theta}} ={\boldsymbol{\varPhi}}\varPsi $$ (3) $$ {\boldsymbol{y}} = {\boldsymbol{\theta}} s $$ (4) 重构原始信号的问题转化为已知y和θ,求解s的数学模型[8]。在求解出s后,由式(1)便可求解出原始信号x。观测矩阵Ф将原始信号x由高维空间投射到低维空间,该过程必然会丢失部分原始信号的信息,因此在求解过程中会面临方程个数远小于未知数个数的情况,直接求解此方程是一个NP-hard问题。陶哲轩等人证明信号满足稀疏性且观测矩阵满足有限等距性等条件时,能够比较精准地求解出s,再通过式(1)可以求解出原始信号[9]。
1.2 压缩超快成像系统
原始图像信号I(x-y-t)在进入条纹相机前,需要先经过DMD的调制。DMD属于一种空间光调制器件,它依靠内部数量众多的微型反射镜来控制光线的反射方向[10],从而实现“光开关”的功能。
DMD有2个稳定的微镜状态(+12°/−12°),在压缩超快成像系统中,通过DMD底层的控制器控制微型反射镜的角度,若控制器内存储单元为“1”,则微型铝镜调整至“+12°”,对应像素的打开状态;若控制器内存储单元为“0”,则微型铝镜调整至“−12°”,对应像素的关闭状态。将DMD对原始图像信号的空间编码看作C,编码后的信号为CI(x-y-t)[10]。
压缩超快成像系统中,采用具有ps时间分辨能力的条纹相机对信号进行探测成像。条纹相机工作原理如图4所示,由变像管(包括光电转换系统、扫描偏转系统、倍增和电光转换系统)和扫描电路组成[11]。
利用压缩超快成像系统对超快场景信号I(x-y-t)进行诊断,首先需要将狭缝完全打开,以取消条纹相机一维空间取样的限制。编码后的图像信号会完全进入条纹相机,不受狭缝的限制。条纹相机内部的光电阴极将输入的光信号转变为相应的电信号,这个过程信号特征参量将线性变换[12]。同时条纹相机中的扫描斜坡脉冲电信号会根据时间线性变化,对编码后的信号起到偏转作用,将条纹相机对编码信号的偏转看作S。偏转后的编码信号为SCI(x-y-t),将此时的信号设定为I'(x'-y'-t),则有:
$$ I'(x' - y' - t) = SCI(x - y - t) $$ (5) I'(x'-y'-t)于条纹相机内部以电子图像的形式存在,电子图像轰击荧光屏转变为可见光图像,该可见光图像被CCD图像传感器进行采集记录。在CCD图像传感器的单次曝光时间T内完成一次成像,信号传播过程中有噪声加入,将噪声对信号的影响设定为n,则CCD图像传感器上最终获得测量信号为M(x'-y')[13]。压缩超快成像系统图像采集过程如图5所示。这个图像采集过程可以理解为压缩超快成像的正向数学模型,即:
$$ \begin{split} M(x' - y') =& TI'(x' - y' - t) + n \\ = &TSCI(x - y - t) + n \end{split} $$ (6) 为方便模型运算,将TSC用O表示为
$$ M(x{'}-y{'})=\text{ }OI(x-y-t)+\text{ }n $$ (7) 为求解原始信号,从压缩超快成像系统测量信号中重构出需要观测的超快场景,既从M(x’-y’)中求解出I(x-y-t),需要反向求解方程组,这是一个欠定数学难题,无法直接求得精确解[14]。由压缩感知理论可知,结合编码矩阵的先验知识,采用基于总变分原理的正则化方法将这个问题转变为无约束优化运算[15],即:
$$ I = {\text{ arg min}}{\Big \{ \frac{1}{2}||M - OI|{|^2} + \lambda \varphi (I)\Big \} ^{}} $$ (8) 式中:λ为正则化参数;φ为正则化函数。无约束优化问题转化为以下有约束优化问题[16]:
$$ (I,P)=\text{ arg min}\Big \{\frac{1}{2}||M-OP||+\lambda \phi (I)\Big \},I=P $$ (9) 通过梯度下降的思路不断迭代上式中的I和P,可以获得局部最优解,从而获得图像的原始信号I(x-y-t)。
2 模拟实验及测量结果
2.1 压缩超快成像图像采集模拟
为了测试压缩超快成像系统对超快场景内原始三维图像信号I(x-y-t)的诊断效果,在Matlab软件中模拟压缩超快成像图像采集过程,对原始三维图像信号进行编码和偏转、重叠的操作,如图6所示。最终由基于压缩感知的还原算法重建原始信号[17]。软件中内置函数生成随机的0~1矩阵作为编码矩阵C,编码矩阵C生成后保持不变,矩阵中元素1占比50%,压缩超快成像系统的采样率为50%。编码矩阵与图像信号相乘,以达到模拟DMD的编码效果。编码过程如图7所示。
条纹相机内偏转电场的场强呈线性均匀变化,不同时刻的图像信号进入条纹相机后,会受到不同偏转电场的偏转作用,成像于CCD竖直方向不同位置。编码后信号的偏转与重叠原理如图8所示。
模拟时采用条纹相机的参数为:极限时间分辨率为10 ps,扫描速度为2 mm/ns,全屏扫描时间为20 ns,圆形荧光屏的有效直径为40 mm。
用于模拟的超快场景是单次脉冲激光在介质中的运动,以及被2个平面镜反射的过程,整个运动轨迹呈Z型。超快三维图像信号时间长度为100 ps,一共由8帧图像组成,每帧图像尺寸为256×256像素,故有I(256,256,8)。其中8张原始图像信号编码后偏转重叠,得到二维测量图像信号M(256×263),如图9 所示。
2.2 压缩超快成像系统还原原始图像
从压缩超快成像系统测量信号中重构原始场景,需要结合随机编码矩阵C的先验知识,求解方程(8),可使用两步迭代收缩/阈值法(two-step iterative shrinkage/thresholding, TWIST),最小化方程中的目标函数,多次迭代得出最优解[18]。每次迭代中,使用一组加权的阈值对信号进行软阈值处理,以产生一个更稀疏的信号。然后,对经过软阈值处理后的信号进行加权反投影操作,生成一个反投影重构。这个反投影重构用于更新加权因子和阈值,在下一次迭代中重复这个过程。TWIST算法主要优点是能够快速收敛并具有较高的重构精度,但存在重构效率较低,迭代的重构信号最优值不一定为全局最优值等缺陷。本文采用在视频压缩和图像处理领域中广泛应用的即插即用总变分(plug-and-play total variation, PnP-TV)算法[19]。相较于传统的TWIST算法,PnP-TV算法在重构图像质量和效率方面都具有优势。它结合了压缩感知和总变差(total variation, TV)正则化方法,用于图像恢复和去噪,将该算法运用于压缩超快成像系统中,具有简单、高效、灵活等特点。PnP-TV方法的基本思想是,将图像重建问题转化为一个优化问题,其中目标函数由两部分组成:数据项(data fidelity term)和正则化项(regularization term)。数据项度量观测数据与重建图像之间的差异,正则化项通常用总变差来量化图像的光滑程度[20]。
具体来说,PnP-TV方法包含以下4个步骤:
1) 数据项。使用非线性算子(例如,逆变换、传感器模拟等)将观测数据投影到图像空间中,得到投影数据,然后,将投影数据与原始图像之间的差异作为数据项。
2) 正则化项。采用总变差正则化项,用于对图像进行光滑约束,从而使重建图像具有更加平滑的结构。总变差是图像中相邻像素之间差异的L1范数。
3) 优化问题。将数据项和正则化项组合成一个优化问题,目标是最小化目标函数。在PnP-TV方法中,通常采用交替方向乘子法等迭代优化算法来求解这个优化问题。
4) 迭代重建。通过迭代优化算法不断更新图像,直到达到收敛条件为止,每次迭代都会根据数据项和正则化项的贡献对图像进行更新。
PnP-TV方法结合了压缩感知的优点,通过少量的观测数据恢复图像,同时在重建过程中加入总变差正则化项,以提高图像的光滑性和去噪效果。其最大优点是,允许将最先进的去噪算法应用于子优化问题的求解过程,无需指定特定的先验,大大提高了算法的灵活性。因此,可以找到一种优秀的去噪算法,并将其插入到PnP-TV算法框架中,提高算法的重建质量。比如,插入广泛用于图像去噪问题的全变异去噪算法,即可实现灵活处理。传统的TWIST算法通常很耗时,并且有许多参数需要手动调节,而PnP-TV算法在重构图像质量和效率方面都具有优势。
根据压缩超快成像测量图像信号,还原算法一共重构出8幅原始二维图像,每幅曝光时间为12.5 ps,如图10所示。
模拟工作中可以通过计算重构图像信号与原始图像信号的峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似系数(structural similarity, SSIM)两项数据来分析图像重建效果[21],计算机重构图像信号过程一共花费13 s,平均PSNR为32 dB,SSIM为0.92。压缩感知是一种新兴的信号采样和重建理论,允许以远远低于传统采样率的方式获取信号,并在后续阶段通过数学算法进行高质量的重建。在压缩超快成像系统中,压缩感知算法重建效果与稀疏表示、测量矩阵密切相关。为了实现图像重建,本文将目标函数中的稀疏先验项设置为L1范数:即最小化稀疏表示的L1范数,使重建图像具有稀疏性,同时使得大部分系数为零,但是其细节和纹理恢复能力有限。因此,重建信号会存在一定的模糊和噪音。仿真结果表明,本文压缩超快成像系统可以较为精准地重构出超快场景动态图像,并实现800亿帧/s的成像速度。
3 结论
利用Matlab软件对压缩超快成像系统进行了模拟仿真,对原始三维图像信号进行编码、偏转、重叠等操作,获得压缩超快成像系统的测量信号。采用PnP-TV还原算法进行原始超快图像信号重构,该算法在每次迭代时选择一个局部最优解来逐步逼近原始信号,从而提高峰值信噪比和结构相似系数。仿真结果表明,压缩超快成像系统具有ps量级的时间分辨能力及800亿帧/s的成像速度,峰值信噪比优于30 dB+,图像相似性系数优于0.91。该系统可应用于超快二维动态过程诊断等领域。
-
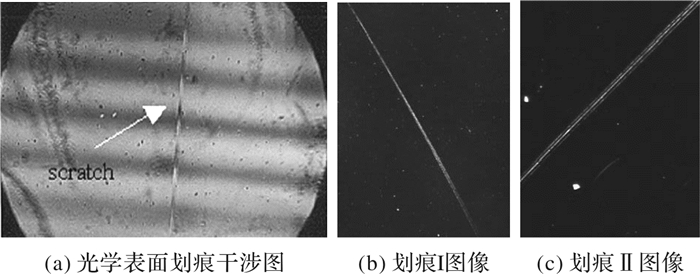
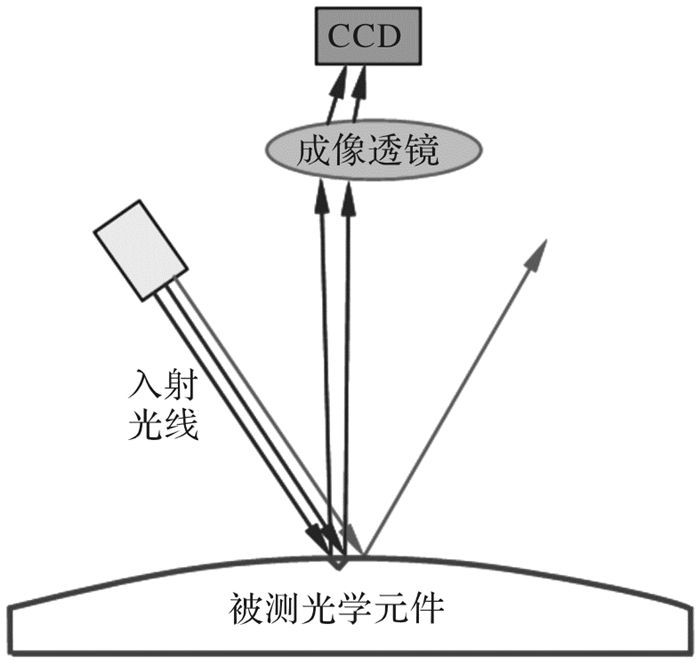
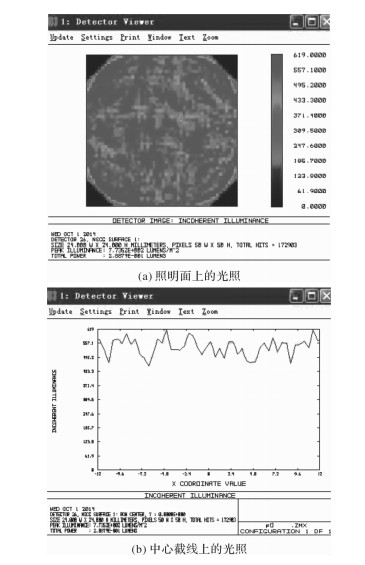
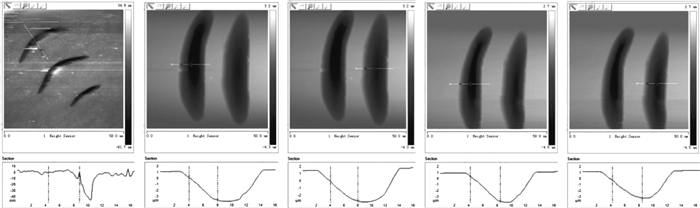
表 1 疵病类别评定表
Table 1 Categories evaluation of surface defects
疵病类别 形状因子 区域填充度 划痕 0~0.48 0.57~0.85 麻点 >0.65 0.65~0.85 灰尘 0.48~0.65 不定 表 2 硅镜疵病图像的识别结果
Table 2 Recognition result of defect images in silicon mirror
类别 总数 总长度/mm 总面积/mm2 划痕 203 76.2 8.58 麻点 30 011 ── 224.49 灰尘 60 023 ── 508.42 -
[1] 李璐, 杨甬英, 曹频, 等.大口径光学元件表面灰尘与麻点自动判别[J].强激光与离子束, 2014, 26(1): 103-108. http://d.old.wanfangdata.com.cn/Periodical/qjgylzs201401022 LI Lu, YANG Yongying, CAO Pin, et al. Automatic discrimination between dusts and digs for large fine optics[J]. High Power Laser and Particle Beams, 2014, 26(1): 103-108. http://d.old.wanfangdata.com.cn/Periodical/qjgylzs201401022
[2] 罗茂, 步扬, 徐静浩, 等.基于多光谱技术的光学元件表面疵病检测[J].中国激光, 2017, 44(1): 0104001. http://d.old.wanfangdata.com.cn/Thesis/Y3157125 LUO Mao, BU Yang, XU Jinghao, et al. Optical element surface defect measurement based on multispectral technique[J]. Chinese Journal of Lasers, 2017, 44(1): 0104001. http://d.old.wanfangdata.com.cn/Thesis/Y3157125
[3] LIU D, WANG S T, CAO P, et al. Dark-field microscopic image stitching method for surface defects evaluation of large fine optics[J]. Optics Express, 2013, 21(5): 5974-5987. doi: 10.1364/OE.21.005974
[4] 朱聪.光学镜片表面疵病检测算法研究[D].成都: 西南交通大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014257473.htm ZHU Cong. Research of the defects detection algorithm on the optics lens surface[D]. Chengdu: Southwest Jiaotong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014257473.htm
[5] WANG S T, LIU D, YANG Y Y, et al. Distorion correction in surfaces defects evaluating system of large fine optics[J]. Optics Communications, 2014, 312(1): 110-116.
[6] DM Tsai, CHEN M C, LI W C, et al. A fast regularity measure for surface defect detection[J]. Machine Vision and Applications, 2012(23): 869-886. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e0f6ec8858c34c30ee4a32e76adf34fc
[7] YANG Y Y, WANG S T, CHEN X Y, et al. Sparse microdefect evaluation system for large fine optical surfaces based on dark-field microscopic scattering imaging[J]. Proc. of SPIE, 2013, 8838: 883806. doi: 10.1117/12.2023438
[8] LIU D, YANG Y Y, WANG L, et al. Microscopic scattering imaging measurement and digital evaluation system of defects for fine optical surface[J]. Optics Communications, 2007, 278(2): 240-246. doi: 10.1016/j.optcom.2007.06.041
[9] DM Tsai, IY Chiang, YH Tsai. A shift-tolerant dissimilarity measure for surface defect detection[J]. IEEE Transactions on Industrial Informatics, 2012, 8(1): 128-137. doi: 10.1109/TII.2011.2166797
[10] LF Fattak. Efficiency of optical non-destructive testing method to detect surface defects in engineering materials[J]. Al-Nahrain Journal for Engineering Sciences, 2015, 18(1): 118-127.
[11] 张彬, 刘缠牢.球面光学元件表面疵病的自动检测技术研究[J].光学仪器, 2013, 35(6): 16-20. doi: 10.3969/j.issn.1005-5630.2013.06.004 ZHANG Bin, LIU Chanlao. Research on automatic detection technology for spherical optical element surface defect[J]. Optical Instruments, 2013, 35(6): 16-20. doi: 10.3969/j.issn.1005-5630.2013.06.004
[12] 陈国, 赵长明, 纪荣祎, 等.基于ZEMAX的半导体激光准直仿真设计[J].激光技术, 2012, 36(3): 318-321, 325. doi: 10.3969/j.issn.1001-3806.2012.03.008 CHEN Guo, ZHAO Changming, JI Rongyi, et al. Simulation design of semiconductor laser collimation based ZEMAX[J]. Laser Technology, 2012, 36(3): 318-321, 325. doi: 10.3969/j.issn.1001-3806.2012.03.008
[13] GAO X, YANG Y Y, ZHAO P, et al. Super-smooth surface defects measurement and evaluation system[J]. Proc. of SPIE, 2010, 7656: 76560A. http://d.old.wanfangdata.com.cn/Periodical/hwyjggc201002029
[14] 付国文.基于Retinex的图像增强算法研究及实现[D].上海: 上海交通大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10248-1011268230.htm FU Guowen. Research and implementation of image enhancement algorithms based on retinex[D]. Shanghai: Shanghai Jiaotong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10248-1011268230.htm
[15] GAO Lingling, FAN Yong, CHEN Niannian, et al. A quick method of debris detecting and classifying for oversize optical element[J]. Microcomputer Information, 2008, 24(9): 306-307, 312.
-
期刊类型引用(2)
1. 蔡厚智,杜卓铭,姚方鼎,刘俊凯,刘进元,向利娟. 条纹变像管压缩超快成像系统研制. 光子学报. 2024(11): 8-17 .  百度学术
百度学术
2. 向利娟,姚方鼎,叶增,刘进元,蔡厚智. 压缩超快成像系统空间分辨特性. 光子学报. 2024(12): 122-132 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载:


















 陕公网安备 61011302001501号
陕公网安备 61011302001501号 