Optimization research based on LED reflective cup system
-
摘要:
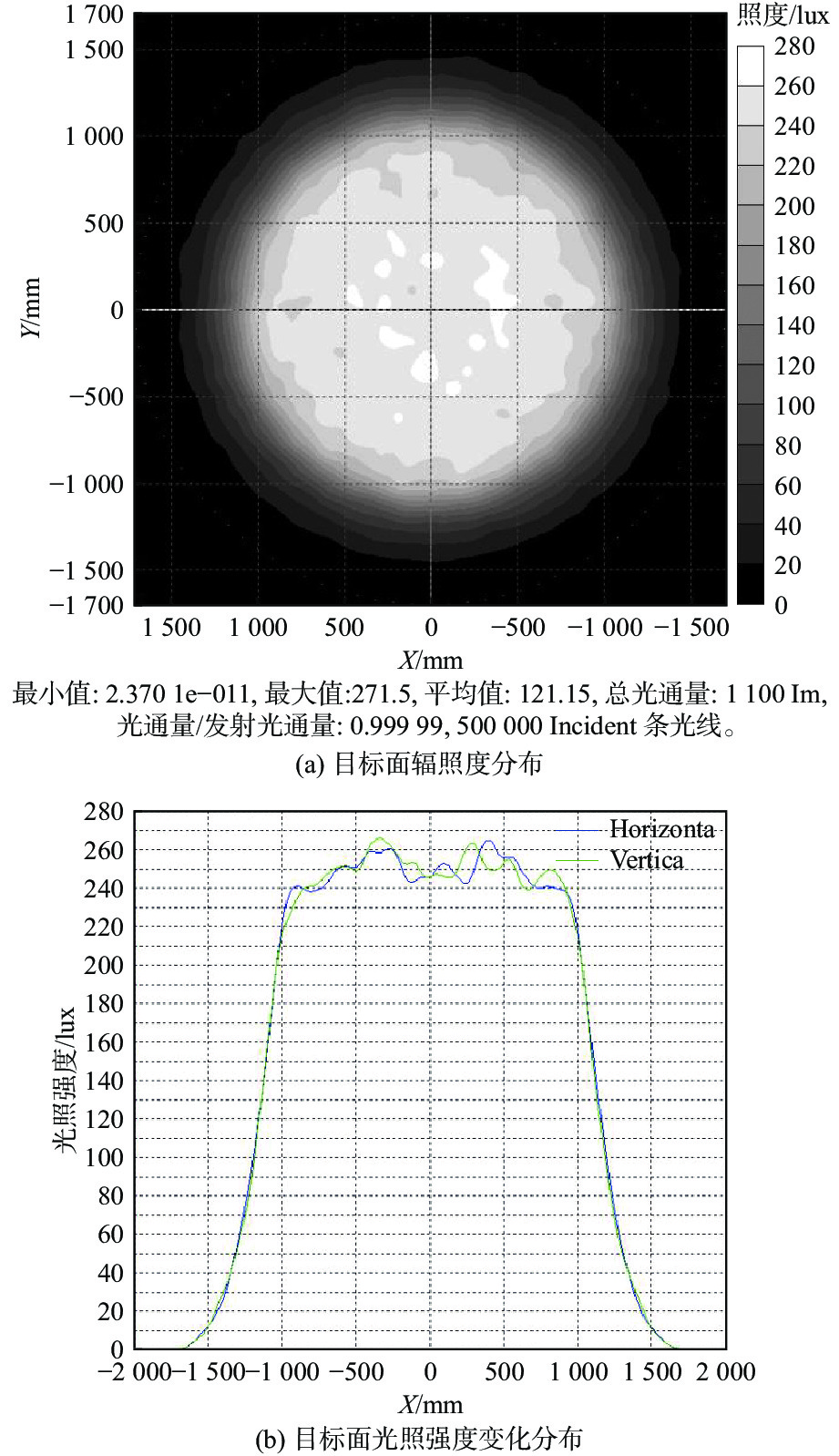
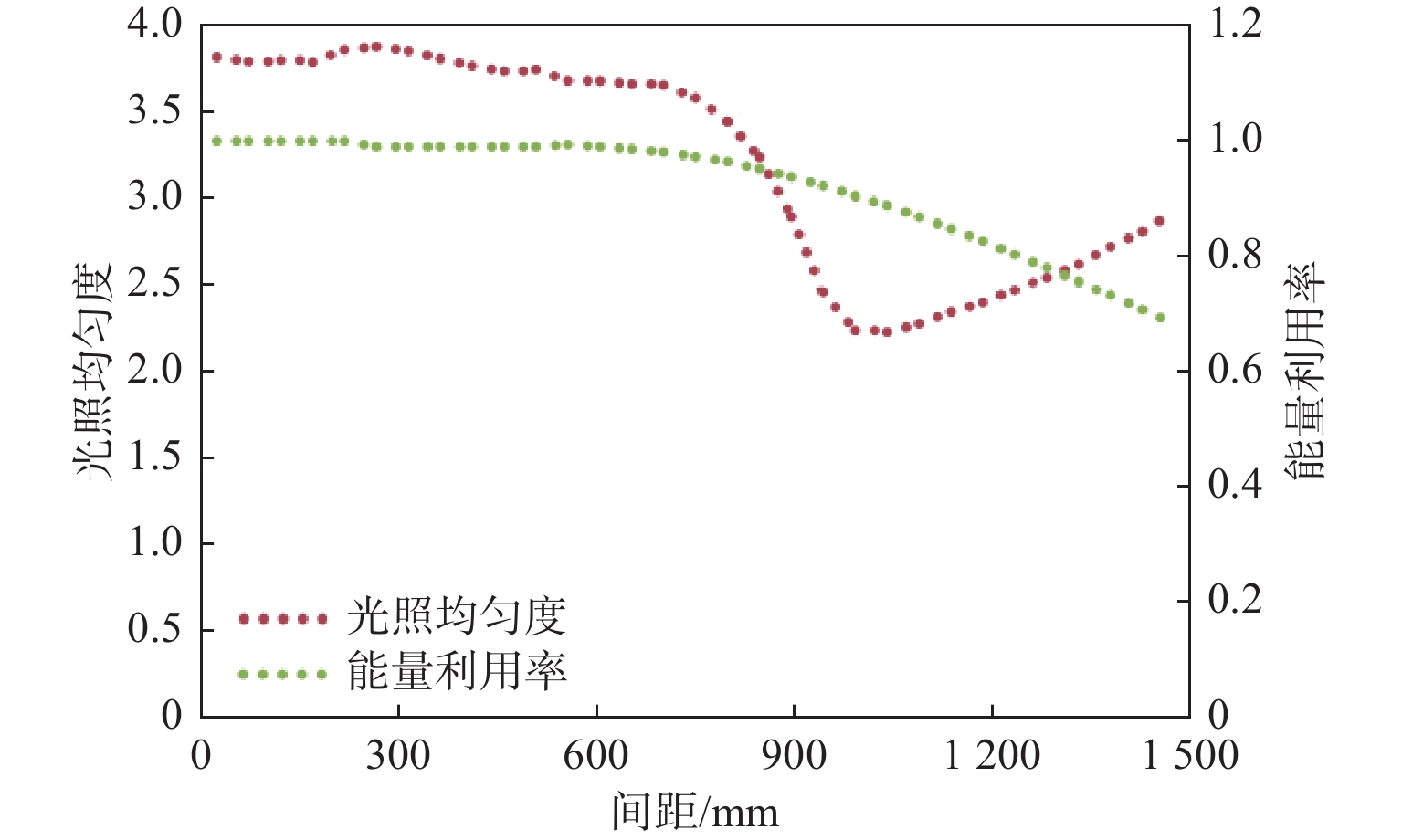
在照明系统设计中,接收面的均匀照明以及光能的充分利用一直是光源设计急需解决的问题。目前在LED光源设计领域中,通常采用斯派罗法则分析和微分方程计算的方式进行照明效果优化,这些方式的优化层面较单一,周期长且误差较大。为了加强LED光源系统优化效率,同步提高光源系统的光照均匀度和能量利用率,论文提出了基于光照均匀度评价函数、能量利用率评价函数和综合性评价函数的优化设计算法。运用数值分析方法对单光源系统的反光杯第二面圆锥常数K与曲率半径R进行优化调整,实现整个反光杯光源系统的光照均匀度和能量利用率的同步优化。研究结果表明:利用该文算法优化后的系统比未优化的光源系统光照均匀度提高了14.2%,能量利用率提高了16.75%,与理想值的接近度提升了14.42%,验证了优化方法的可行性。在此基础上,论文进一步研究多光源系统阵列间距对系统光照均匀度和能量利用率的影响,得出光源阵列系统的最优阵列间距,在此间距下的光照均匀度与理想值的接近度为44.84%,能量利用率为88.84%,最终实现了光照均匀度和能量利用率均较好的矩形阵列光源系统。
Abstract:In the design of lighting system, the uniform lighting of the receiving surface and the full use of light energy have always been urgent problems in the light source design. At present, in the field of LED light source design, the Sparrow Criterion analysis and differential equation calculation are usually used to optimize the lighting effect. The optimization level of these methods is relatively single, with a long cycle and a large error. In order to strengthen the optimization efficiency of the LED light source system and synchronously improve the illumination uniformity and energy utilization rate of the light source system, an optimization design algorithm based on the illumination uniformity evaluation function, energy utilization evaluation function and comprehensive evaluation function was was proposed. Firstly, the numerical analysis method was used to optimize and adjust the conical constant K and curvature radius R of the second side of the single light source system, so as to realize the synchronous optimization of the illumination uniformity and energy utilization rate of the whole reflective cup light source system. The study results show that the optimized system with the algorithm increased by 14.2%, the energy efficiency increased by 16.75%, and the proximity to the ideal value increased by 14.42%, which verifies the feasibility of the optimization method. On this basis, the influence of multi-light source system array spacing for illumination uniformity and energy utilization system was further studied, the optimal array spacing of light source array system, under the distance of the illumination uniformity and the ideal value proximity is 44.84%, energy utilization rate is 88.84%, finally achieving a LED light system in rectangular array with high uniformity and energy utilization.
-
引言
机载光电稳定平台一般由光电载荷、陀螺、框架结构、驱动及控制系统等组成,是一种光、机、电高度集成的军用光电设备,用于目标的侦察和跟踪等。“十四五”规划对于军事装备的性能提出了更高的要求,如探测距离、目标跟踪精度和成像质量等,具体到武器光电稳定平台即是平台的视轴稳定精度[1]。提高平台的抗干扰能力,增强鲁棒性,成为提高光电稳定平台稳定精度的关键。提高速度环的带宽、改进速度环的控制算法则是重点突破方向。高精度电机伺服控制的问题主要有以下3点:摩擦与外力干扰的抑制能力,系统性能受参数变化的影响,系统动态跟踪性能。为此形成3个主要研究领域:前馈跟踪控制、闭环控制策略和摩擦补偿技术。
传统的伺服控制系统已经不能满足要求,为此科研工作者开始探索在传统PID控制策略的基础上,对PID控制技术的算法进行改进,以满足光电稳定平台的性能要求。近年来涌现出多种不同的方法:利用BP神经网络的自学习能力来实现参数在线自整定和优化的PID控制器[2],采用高斯型RBF神经网络对摩擦进行观测和补偿[3],基于神经网络的状态观测器设计陀螺稳定平台控制系统[4]。这些方法设计过程复杂、计算繁琐、成本大、可实现难度高并没有得到推广应用。自从韩京清教授提出自抗扰控制技术[5]以来,在这方面的研究也层出不穷,文献[6]提出基于重复-自抗扰控制技术提高系统的扰动隔离度,文献[7]提出基于模型设计的线性自抗扰控制器提高光电的响应速度和扰动抑制能力。
变结构控制的研究始于20世纪50年代,前苏联学者Emelyanov等提出了变结构控制概念,随后Utkin和Itkis等学者总结并发展了滑模变结构控制理论,奠定了滑模变结构控制的理论基础。在实际控制系统,变结构控制在滑动模态下总伴随着高频抖动,抖动会影响控制精度,我国高为炳院士在变结构控制理论研究中首次提出了趋近律、品质控制、切换模式等新概念,以此消除抖动[8]。滑模变结构控制(sliding mode variable structure control,SMVSC)适用于线性系统和非线性系统的鲁棒控制。本文以两轴四框架光电吊舱为研究对象,对于传统PID控制技术难以较好地解决超调和快速性之间的矛盾,设计一种能够独立于输出控制、抑制各种干扰的控制器,提高系统的干扰抑制能力,实现对光电稳定平台高精度控制。最后通过仿真实验验证该控制策略的有效性,具有抗干扰能力强、稳定精度高和实现简单等优点。
1 光电稳定平台结构及模型
1.1 光电稳定平台结构分析
机载光电跟踪稳定平台发展至今已经有多种框架结构。两轴两框架是航空侦察平台中较为广泛的一种,技术较为成熟,是将光电传感器等侦察设备置于相互正交的俯仰、方位2个框架组成的平台上,如图1所示。通过陀螺稳定回路,克服外干扰力矩,达到视轴稳定的目的[9]。因二框架系统仅适用于小负载、中高精度的稳定平台,其跟踪的角度范围有限,无法很好地解决过顶问题,容易造成自锁丢失目标,跟踪只能实现瞄准线的轴线稳定,而不能实现瞄准线绕自身轴系的旋转变化稳定,同时由于飞机姿态摇摆幅度及摇摆方向的随机性,致使光电成像图像曲变,后期处理困难。三框架三轴稳定平台克服了两轴两框架稳定平台系统的缺点,其稳定原理是根据载体摇摆参数和瞄准空间参数计算出跟踪轴角状态参数,驱动跟踪伺服机构实现瞄准线稳定,控制过程复杂,同时由于捷联式三轴稳定跟踪台工作时对象呈现出非线性、强耦合和参数变化等特点,因此系统在稳态精度、响应时间、稳定性等方面的要求较高[10]。
两轴四框架是在两轴两框架的基础上增加一个内框架,与上述2种结构相比具有以下特点:1) 内框架始终保持垂直,减小耦合作用,隔离好,可消除俯仰大角度运动情形下的自锁现象,提高稳定精度;2) 内外环控制回路相互独立,互不影响,且方位和俯仰回路伺服机制完全相同,设计相对容易;3) 经过标准配平后负载力矩小,系统带宽增加,利于提高系统精度,且生产成本具有优势。因此本文选择两轴四框架结构方案,如图2所示。
1.2 光电稳定平台模型分析
两轴四框架光电稳定平台控制系统可以分为方位轴和俯仰轴2个相互独立的系统,而且2个通道的控制策略基本相同,因此本文只论证方位轴的控制。方位轴伺服控制回路控制框图如图3所示,主要包括控制器、功率放大器、电机及框架负载、陀螺、编码器。
为达到高精度、响应快、强鲁棒性要求,伺服控制采用电流环、速度环和位置环构成三闭环级联复合控制。其中,由陀螺反馈构成的速度环才是补偿扰动与提升光电稳定平台控制精度的关键部分。光电稳定平台单轴控制速度环的数学模型如图4所示。
图4中,
${\theta _i}$ 为给定的角度指令信号,$ {w}_{0} $ 为给定的速度指令信号,${\theta _O}$ 为框架输出角度,$ {T}_{L}\left(s\right) $ 为干扰力矩,$f$ 为摩擦力矩,${K_{{\rm{TV}}}}{e^{ - \tau {\rm{TV}}}}$ 为电视调节器,$K{G_1}(s)$ 为位置控制器,$ {G}_{v}\left(s\right) $ 为速度环伺服控制器,$ {k}_{PWM} $ 为功率放大系数,$ {k}_{g} $ 为陀螺,$ {L}_{a}$ 、$ {R}_{a} $ 为电枢电感与电枢电阻,${C_m}$ 、${C_e}$ 、${J_a}$ 为电机的转矩系数、反电动势系数和转动惯量。依据其物理特性,每个自由度的动态机电模型可以简化为
$$J\ddot \theta + b\dot \theta = u{+ d + }\Delta {(x,t)}$$ (1) $$\ddot \theta {\rm{ = - }}\dfrac{b}{J}\dot \theta + \dfrac{1}{J}u(t) + \dfrac{1}{J}(d(t) + \Delta (x,t))$$ (2) 式中:
$J$ 为转动惯量;$b$ 为阻尼系数;$u$ 为控制输入;θ、$ \dot{\theta }$ 为角位置和角速度;$d$ 为系统的外界干扰,包含摩擦干扰、不平衡力矩等;$ \Delta(x,t) $ 为系统的未知不可建模的非线性动态部分。2 新型非线性扩张观测器的滑模控制器设计
2.1 新型非线性扩张观测器设计
扩张观测器的核心思想是把光电平台的外部扰动和内部扰动共同作为总扰动,将其扩张为系统新的状态变量,通过构建的状态观测器(ESO)估计出系统的总扰动,实时补偿给系统得以准确抑制。传统的线性扩张观测器对于各个状态量
${x_i}$ 以及系统的干扰d估计精度较低且误差收敛速度较慢。线性高增益扩张观测器是通过引入足够大的高增益误差反馈,使观测器的动态远远高于系统的动态,从而提高观测误差的估计精度和收敛速度。但其也存在由于增益系数非常大,在实际工程应用中会把测量噪声放大,影响系统状态变量和误差干扰估计的精准性的缺点。因此将非线性增益引入到ESO中,即形成非线性扩张观测器(nonlinear extended state observer,NESO),在提高误差收敛速度和估计精度的同时,尽量减小对系统的影响。设光电跟踪平台为非线性时变系统,本文将结合NESO和有限时间收敛理论提出一种新型非线性扩张观测器(novel nonlinear extended state observer,NNESO)的设计方法。(2)式的非线性动态的状态空间描述形式为
$$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2} \;} \\ {{{\dot x}_2} = - \dfrac{b}{J}{x_1} + \dfrac{1}{J}u(t) + d(t)} \\ {y = {x_1} } \end{array}} \right.$$ (3) 式中:
$x = {[{x_1} {x_2}]^{\rm{T}}}$ 为系统状态变量;$u(t)$ 为控制输入;$d(t)$ 为系统总扰动。根据(3)式把d(t)扩张成新的状态变量x3,其非线性扩张状态观测器形式为
$$\left\{ {\begin{array}{*{20}{l}} {e = {x_1} - {{\hat x}_1} } \\ {{{\dot{\hat{x}}}_1} = {{\hat x}_2} + {\beta _1}{f_1}(e)} \\ {{{\dot{\hat{x}}}_2}{\rm{ = }}{{\hat x}_3} + {\beta _2}{f_2}(e)} \\ {{{\dot{\hat{x}}}_3}{\rm{ = }}{\beta _3}{f_3}(e) } \end{array}} \right.$$ (4) 式中:
${\hat x_i}$ 为状态变量观测值;e为观测误差;${f_i}(e)$ 为非线性函数;增益系数满足$[{\beta _1},{\beta _2}, \cdots ,{\beta _{n + 1}}] = $ $ [{\omega _o}{\alpha _1},{\omega _o}{\alpha _2}, \cdots ,{\omega _o}{\alpha _{n + 1}}]$ 关系。采用带宽确定线性扩张观测器参数的算法,根据特征多项式定理可以推知${s^{n + 1}} + {\omega _0}{\alpha _1}{s^n} + \cdots + \omega _{_0}^n{\alpha _n}s + \omega _{_0}^{n + 1}{\alpha _{n + 1}} = {(s + {\omega _0})^{n + 1}}$ ,其中${\omega _0}$ 为观测器带宽唯一可以调节的参数,${\omega _0}$ 的选取直接影响到干扰估计的精度与收敛速度。二阶对象中${\beta _1} = 3{\omega _0}$ ,${\beta _2} = 3{\omega _0}^2$ ,${\beta _3} = \omega _0^3$ ,根据系统的观测性和稳定性综合选取,工程实际应用中${\omega _0} > 1$ 。为了避免仿真时出现高频颤振现象,可利用非线性函数在原点附近具有线性段连续幂次函数的特性,即
${f_i}(e) = fal(e,h,\delta ) = \left\{ {\begin{array}{*{20}{c}} {{{\left| e \right|}^h}{\rm{sign}}(e),\quad \left| e \right| > \delta } \\ {\dfrac{e}{{{\delta ^{1 - h}}}},\quad \quad \quad \left| e \right| \leqslant \delta } \end{array}} \right.$ ,其中0<h<1,$2\delta $ 为$fal(e,h,\delta )$ 函数中线性段区间的长度,如图5所示。根据(4)式结合有限时间收敛理论可以设计出新型非线性扩张观测器:
$$\left\{ {\begin{array}{*{20}{l}} {e = {x_1} - {{\hat x}_1} \;} \\ {{{\dot{\hat{x}}}_1} = {{\hat x}_2} + {\beta _1}({{\left| e \right|}^{{p_1}}}{\rm{sign}}(e) + {{\left| e \right|}^{{g_1}}}{\rm{sign}}(e)) + {k_1}{\rm{sign}}(e) \;} \\ {{{\dot{\hat{x}}}_2}{\rm{ = }}{{\hat x}_3} - \dfrac{b}{J}{{\hat x}_2} + \dfrac{1}{J}u + {\beta _2}({{\left| e \right|}^{{p_2}}}{\rm{sign}}(e) + {{\left| e \right|}^{{g_2}}}{\rm{sign}}(e)) +} \\ \quad\quad{{k_2}{\rm{sign}}(e)} \\ {{{\dot{\hat{x}}}_3}{\rm{ = }}{\beta _3}({{\left| e \right|}^{{p_3}}}{\rm{sign}}(e) + {{\left| e \right|}^{{g_3}}}{\rm{sign}}(e)) + {k_3}{\rm{sign}}(e) } \end{array}} \right.$$ (5) 式中:
${\hat x_i}$ 是状态变量${x_i}$ 的估计值;${\hat x_3}$ 是总扰动d(t)估计值;$1 < {\beta _i} < + \infty $ ;$\dfrac{2}{3} < {p_1} < 1$ ,${p_i} = i{p_1} - (i - 1)$ ,$1 < $ $ i \leqslant 3$ ;${g_1} = \dfrac{1}{{{p_1}}}$ ,${g_i} = {g_1} + (i - 1)({p_1} - 1)$ ,$1 < i \leqslant 3$ ;${k_i} > 0$ 。在(5)式中${\left| e \right|^{{p_i}}}{\rm{sign}}(e)$ 和${\left| e \right|^{{g_i}}}{\rm{sign}}(e)$ 是连续可微的函数,而$ {{k}_{i}}\centerdot {\rm{sign}}(e)$ 是不连续的,这将会造成当e在零附近频繁变化时出现颤振(抖振)现象。因此,使用${\rm{sigmoid}}$ 函数来代替,即:$${\rm{sgmf}}(e) = \left\{ {\begin{array}{*{20}{c}} {2\left( {\dfrac{1}{{1 + {{\exp }^{ - \tau e}}}} - \dfrac{1}{2}} \right)},\quad \left| e \right| \leqslant \varepsilon \\ {{\rm{ sign}}(e),\quad \quad \left| e \right| > \varepsilon } \end{array}} \right. $$ (6) 式中:
$\varepsilon $ 为边界层;$\tau $ 是反比与$\varepsilon $ 的常数。观测器带宽设置是控制器带宽的3~5倍。2.2 滑模控制器设计
系统在SMVSC控制器中可对干扰进行补偿,使得切换增益降低,有效降低了切换带来的抖动问题。系统的控制目标是
$ \theta \to {\theta }_{d},\dot{\theta }\to {\dot{\theta }}_{d} $ ,因此设计滑模切换函数为$s = ce + \dot e$ 。其中,$ c>0 $ (c值决定收敛速度),$ e={\theta }_{d}-\theta $ 为跟踪误差。由系统模型可以推导出:
$$\ddot e = {\ddot \theta _d} - \ddot \theta = {\ddot \theta _d} - \dfrac{1}{J}( - b\dot \theta + u + d)$$ (7) $$\dot s = c\dot e + \ddot e = c\dot e + {\ddot \theta _d} + \dfrac{{b}}{J}\dot \theta - \dfrac{1}{J}u - \dfrac{1}{J}d$$ (8) 对于滑模变结构控制可取控制律为
$$u(t) = J(c\dot e + {\ddot \theta _d} + \dfrac{b}{J}\dot \theta - \dfrac{1}{J}\hat d + ks + \eta {\rm{sgn}} s),k > 0$$ (9) 则得出:
$$\dot s = - ks - \eta {\rm{sgn}} s - \dfrac{1}{J}\tilde d$$ (10) 闭环系统的李雅普诺夫函数为
$$V = \dfrac{1}{2}{s^2} + \dfrac{1}{2}{\tilde d^2}$$ (11) 根据(7)式和(11)式可得
$$\begin{array}{l} \dot V = s\dot s + \tilde d{\dot{\tilde{d}}} = s( - ks - \eta {\rm{sgn}} s - \dfrac{1}{J}\tilde d) - K{{\tilde d}^2} \\ \quad \;\; - k{s^2} - \eta \left| s \right| - \dfrac{1}{J}\tilde ds - K{{\tilde d}^2} \leqslant 0 \end{array} $$ (12) 式中
$\eta \geqslant \dfrac{1}{J}{\left| {\tilde d} \right|_{\max }}$ 为切换项增益。扩张观测器初始观测误差可取$\left| {\tilde d(0)} \right| = {\left| {\tilde d} \right|_{\max }}$ ,因此取$\eta \geqslant \dfrac{1}{J}\left| {\tilde d(0)} \right|$ 。控制系统的收敛性可表示为
$$\begin{array}{l} \dot V = - k{s^2} - \eta \left| s \right| - \dfrac{1}{J}\tilde ds - K{{\tilde d}^2} \leqslant - k{s^2} - K{{\tilde d}^2} \\ \quad \; \leqslant - {k_1}\left( {\dfrac{1}{2}{s^2} + \dfrac{1}{2}{{\tilde d}^2}} \right) = - {k_1}V \end{array} $$ (13) 式中
$ {k_1} = 2\min \{ k,K\}$ 。针对
$ V:[0,\infty )\in R, $ 不等式$ \dot{V}\leqslant -\alpha V+f, \forall t\geqslant {t}_{0}\geqslant 0 $ 的解[11]为$$V(t) \leqslant {e^{ - \alpha (t - {t_0})}}V({t_0}) + \int_{{t_0}}^t {{e^{ - \alpha (t - \tau )}}} w(\tau ){\rm{d}}\tau $$ (14) 式中
$\alpha $ 为任意常数。根据(14)式可以解出(13)式,
$ V\left(t\right)\leqslant {e}^{-{k}_{1}(t-{t}_{0})}\times $ $ V\left({t}_{0}\right) $ 。由此可知方位轴系统指数收敛,其收敛精度取决于$ {k}_{1} $ 值的大小。3 实验结果分析
3.1 扩张观测器实验分析
为验证扩张观测器对不确定干扰估计的有效性,本文在仿真实验中对于慢变化干扰、快变化干扰及不确定干扰,线性高增益扩张观测器、非线性扩张观测器、以及改进型非线性扩张观测器的实现结果进行综合对比,3种不同扩张观测器作用对比控制框图如图6所示。NNESO的相关参数选取
${\beta _1}{\rm{ = }}100$ ,${\beta _2}{\rm{ = }}200$ ,${\beta _3}{\rm{ = }}2\;500$ ,${p_1}{\rm{ = }}0.9$ ,${p_i} = i{p_1} - (i - 1)$ ,$1 < i \leqslant 3$ ;${g_1} = \dfrac{1}{{{p_1}}}$ ,${g_i} = {g_1} + (i - 1)({p_1} - 1)$ ,$1 < i \leqslant 3$ 及${k_1}{\rm{ = 6}}$ ,${k_2}{\rm{ = 300}}$ ,${k_3}{\rm{ = 9}}\;{\rm{000}}$ 。线性高增益扩张观测器(LHESO)与非线性扩张观测器(NESO)相关参数选取相同,另外NESO中的其他参数$\tau {\rm{ = }}45$ ,$\delta {\rm{ = 0}}{\rm{.05}}$ 。实验1。加入
$d = 0.5 \times \sin (0.5{\rm{{\text{π}}}}t)$ 慢变干扰,仿真实验结果如图7所示。此实验验证对比3种干扰补偿方法对慢变干扰的估计。从图7可看出,LHESO、NESO、NNESO 3种估计方法的稳态误差为0.03、0.023、0.0015,表明NNESO对于干扰估计具有高有效性。
实验2。加入
$d = 0.5 \times \sin (10{\rm{{\text{π}} }}t)$ 快变干扰,仿真实验结果如图8所示。此实验验证对比3种干扰补偿方法对快变干扰的估计。从图8可看出,LHESO、NESO、NNESO 3种估计方法的稳态误差为0.37、0.43、0.03,表明LHESO、NESO对快干扰几乎失效,而NNESO对于干扰估计仍然具备有效性。
实验3。加入
$d = \dfrac{3}{5} \times {\rm{exp(cos(6}}t{\rm{))}} \times {\rm{sin(7{\text{π}} }}t{\rm{) + }}\dfrac{1}{2} \times $ $ {\rm{exp( - cos(0}}{\rm{.8}}t{\rm{))}} \times {\rm{cos(2{\text{π}} }}t{\rm{) + sin({\text{π}} }}t{\rm{)}}$ 复杂不确定干扰(包含摩擦力矩、陀螺噪声及系统参数变化),仿真实验结果如图9所示。此实验验证对比3种干扰补偿方法对不确定干扰的估计。从图9可看出,LHESO、NESO、NNESO 3种估计方法的稳态误差为0.78、0.68、0.014,表明LHESO、NESO对干扰几乎失效,而NNESO对于干扰估计仍然具备有效性。
总上所述,设计的新型非线性扩张观测器性能皆优于线性高增益扩张观测器和传统非线性扩张观测器,并能够满足滑模控制的快速切换特性,对动态干扰和参数变化都能有效进行估计。
3.2 闭环控制系统结果分析
针对两轴四框架光电稳定平台SMC+NNESO控制策略的有效性按照图10所示结构形式进行仿真验证。模型参数
$J=0.002\; 4$ ,$b=0.071 \;4$ 。控制系统中加入正弦动态干扰信号作为对外界的其他干扰因素。同时,由于摩擦是干扰力矩的主要来源,低速和换向时,静摩擦和动摩擦来回交替会使运动不流畅,称为爬行现象。在高速时,由于摩擦的过阻尼特性会使实际速度低于期望速度。为此需要在仿真实验中加入Lugre摩擦模型[11]:$$\left\{ {\begin{array}{*{20}{l}} {F = \dfrac{1}{J}({\sigma _0} {\textit{z}} + {\sigma _1}\dot {\textit{z}} + \alpha \dot \theta ) \;} \\ {\dot {\textit{z}} = \dot \theta - \dfrac{{{\sigma _0}\left| {\dot \theta } \right|}}{{g(\dot \theta )}} {\textit{z}} } \\ {g(\dot \theta ) = {F_C} + ({F_S} - F_C^{}){e^{ - {{\left(\tfrac{{\dot \theta }}{{{V_S}}}\right)}^2}}} + \alpha \dot \theta } \end{array}} \right.$$ (15) 式中:
$ {\sigma }_{0} $ 、$ {\sigma }_{1,}$ 是动态摩擦参数,取值为${\sigma _0} = 130$ ,${\sigma _1} = 1.8$ ;${F_C}$ 、${F_S}$ 、$\alpha $ 、${V_S}$ 是静态摩擦参数,取值${F_C} = 0.32$ ,${F_S} = 0.29$ ,$\alpha = 0.02$ ,${V_S} = 0.01$ 。为了验证系统动态情况下的性能,输入位置指令
$ {\theta }_{d}=3\times {\rm{sin}}t $ 正弦信号,首先观察加入系统干扰时SMC闭环控制误差状态,再观测SMC+NNESO控制作用下系统的位置跟踪输出、控制量输出、位置跟踪误差和角速度误差状态,实验结果如图11和图12所示。从图11可看出,位置响应在0.1 s后跟踪误差降为0.000 4,速度响应在0.18 s后与理想期望值相等。从图11和图12(c)、12(d)的对比可以看出,闭环系统再加入非线性扩张观测后能够将干扰估计值补偿给控制器,所以系统一旦进入稳态跟踪误差基本为零。而仅SMC控制的回路无法获知干扰,干扰一直无法补偿,因此跟踪误差将一直存在。SMC控制闭环系统位置,速度跟踪响应曲线因为与SMC+NNESO控制的响应曲线基本一致,无法直接观察出,因此为避免造成误解未列出。
最后对加入周期突变干扰后的SMC+NNESO控制系统进行实验,实验结果如图13所示。从图13中可看出,位置响应在0.5 s后跟踪误差降为0.005 3,由于突变干扰影响,速度响应在0.2 s内调节与理想期望值相等。
从图12和图13可以看出,光电跟踪平台闭环系统采用此种控制策略跟踪性能明显提高,且跟踪误差波动明显减小,滑模切换抖动减小,提高了整个控制系统的稳定性、快速性。
为验证系统整机的控制效果,在直升机低频0.01 Hz~1 Hz振动条件下进行稳定精度仿真分析,结果如图14和图15所示。
为验证滑模变结构与新型非线性扩张观测器复合控制算法的实际效果,在某机场附近对起飞/降落飞机进行稳定跟踪实验,实验结果如图16所示。
综上所述,可计算出光电跟踪平台系统稳定精度为
$\sqrt {{{49}^2} + {{56}^2}} = 74.4$ µrad,优于100 µrad,且在外场实测过程中表现良好,验证了本文改进方法不仅具有理论研究意义,而且对于工程实用也具有推动作用。4 结论
通过仿真实验证明了本文提出的控制方法的可行性,能够满足高精度光电跟踪平台系统的技术要求,同时与文献[12]~[15]相比,改进的方法可使基于指数趋近律的滑模控制系统,利用新型非线性扩张观测器将干扰补偿到控制输入中,能够削弱抖动问题,增强光电跟踪平台性能。相比文献[16]和[17],本文提出的控制策略可快速估计出干扰,且将干扰应用到光电稳定平台的补偿环节中,使得系统对参数摄动及复杂非线性干扰具有强鲁棒性,较好地保证了整个伺服控制系统的平稳性和跟踪精度。在光电稳定平台的实际工程应用中多采用PID控制、自抗扰控制、滑模变结构等,此种级联复合控制方法采用传统的控制算法,本文提出的改进方法在可靠性,环境适应性方面还需要进行大量的整体调试实验验证。
-
表 1 优化数据统计表
Table 1 Optimization data statistics
综合评价
函数值光照均匀度
评价函数值能量利用率
评价函数值曲率半径/mm 圆锥常数 最优曲率
半径/mm最优圆锥常数 最优综合
评价函数值2.240 9 2.240 9 1 32 −0.9 32 −0.9 2.240 9 3.153 9 3.050 8 0.8968 32 −0.966 7 32 −0.9 2.240 9 3.562 7 3.370 3 0.8076 32 −1.033 3 32 −0.9 2.240 9 3.865 2 3.607 2 0.7419 32 −1.1 32 −0.9 2.240 9 2.270 2 2.268 3 0.9980 32.666 7 −0.9 32 −0.9 2.240 9 3.180 8 3.066 3 0.8854 32.666 7 −0.966 7 32 −0.9 2.240 9 3.613 7 3.411 7 0.7979 32.666 7 −1.033 3 32 −0.9 2.240 9 3.906 0 3.640 2 0.7341 32.666 7 −1.1 32 −0.9 2.240 9 2.322 3 2.313 1 0.9908 33.333 3 −0.9 32 −0.9 2.240 9 3.200 8 3.074 6 0.8739 33.333 3 −0.966 7 32 −0.9 2.240 9 3.652 6 3.441 1 0.7885 33.333 3 −1.033 3 32 −0.9 2.240 9 3.927 2 3.653 4 0.7262 33.333 3 −1.1 32 −0.9 2.240 9 2.383 8 2.363 6 0.9798 34 −0.9 32 −0.9 2.240 9 3.246 3 3.109 1 0.8627 34 −0.966 7 32 −0.9 2.240 9 3.673 8 3.453 2 0.7795 34 −1.033 3 32 −0.9 2.240 9 3.924 8 3.643 3 0.7184 34 −1.1 32 −0.9 2.240 9 -
[1] 明振兴, 吕清花, 明月, 等. 基于改进粒子群算法的LED光源阵列优化[J]. 应用光学,2022,43(3):524-531. doi: 10.5768/JAO202243.0305003 MING Zhenxing, LYU Qinghua, MING Yue, et al. Optimization of the LED light source array based on an improved particle swarm algorithm[J]. Journal of Applied Optics,2022,43(3):524-531. doi: 10.5768/JAO202243.0305003
[2] 周彦辰, 郭亮, 陈志涛, 等. 基于全内反射结构的多自由曲面准直透镜设计[J]. 光学学报,2021,41(4):186-194. ZHOU Yanchen, GUO Liang, CHEN Zhitao, et al. Design of multi-free surface collimation lens based on full internal reflection structure[J]. Acta Optica Sinica,2021,41(4):186-194.
[3] 黄日带. 大功率LED灯在体育建筑照明中的应用[J]. 照明工程学报,2020,31(1):83-86. doi: 10.3969/j.issn.1004-440X.2020.01.015 HUANG Ridai. Application of high-power LED lamp in sports building lighting[J]. China Illuminating Engineering Journal,2020,31(1):83-86. doi: 10.3969/j.issn.1004-440X.2020.01.015
[4] 张勇, 刘卫平, 马飒飒, 等. 大视场低照度夜视头戴目镜光学系统设计[J]. 应用光学,2023,44(3):636-642. doi: 10.5768/JAO202344.0304002 ZHANG Yong, LIU Weiping, MA Sasa, et al. Design of eyeoptical system for large field and low illumination[J]. Journal of Applied Optics,2023,44(3):636-642. doi: 10.5768/JAO202344.0304002
[5] 杨超, 宋国华, 范婷婷, 等. 针对LED扩展光源照明的自由曲面透镜设计[J]. 光学技术,2022,48(2):129-134. doi: 10.3321/j.issn.1002-1582.2022.2.gxjs202202001 YANG Chao, SONG Guohua, FAN Tingting, et al. Freeform lens design for LED extended light source illumination[J]. Optical Technology,2022,48(2):129-134. doi: 10.3321/j.issn.1002-1582.2022.2.gxjs202202001
[6] BAI J, LI X, HU L, et al. Research on illumination uniformity in edible mushrooms incubator with genetic algorithm[J]. Optik,2021,239:166862. doi: 10.1016/j.ijleo.2021.166862
[7] 刘晓茵, 杨磊, 杨童, 等. 微小球面显微光学系统设计与照明分析[J]. 应用光学,2023,44(2):262-267. doi: 10.5768/JAO202344.0201004 LIU Xiaoyin, YANG Lei, YANG Tong, et al. Design and illumination analysis[J]. Journal of Applied optics,2023,44(2):262-267. doi: 10.5768/JAO202344.0201004
[8] 甘勇, 贾崔赟. 基于TracePro的发光二极管均匀照明光源设计[J]. 科学技术与工程,2020,20(31):12808-12813. doi: 10.3969/j.issn.1671-1815.2020.31.019 GAN Yong, JIA Cuiyun. Design of luminous diode uniform illumination light source based on TracePro[J]. Advanced Engineering Science,2020,20(31):12808-12813. doi: 10.3969/j.issn.1671-1815.2020.31.019
[9] ZHANG Q, GAO J, CHEN X. Influence of optical aspheric parameters on obtaining uniform rectangular illumination[J]. Optik,2014,125(11):2577-2581. doi: 10.1016/j.ijleo.2013.11.017
[10] 夏勋力, 余彬海, 麦镇强. 近朗伯光型LED透镜的光学设计[J]. 光电技术应用,2010,25(1):22-25. doi: 10.3969/j.issn.1673-1255.2010.01.007 XIA Xunli, YU Binhai, MAI Zhenqiang. Optical design of a near-Lambert light-type LED lens[J]. Application of Photoelectric Technology,2010,25(1):22-25. doi: 10.3969/j.issn.1673-1255.2010.01.007
[11] 王海洋, 金志樑, 王沛沛, 等. 用于LED光源的反光杯准直效果研究[J]. 照明工程学报,2021,32(1):1-4. doi: 10.3969/j.issn.1004-440X.2021.01.016 WANG Haiyang, JIN Zhiliang, WANG Peipei, et al. Study on the collimation effect of reflective cup used for LED light source[J]. China Illuminating Engineering Journal,2021,32(1):1-4. doi: 10.3969/j.issn.1004-440X.2021.01.016
[12] 樊冬新, 刘鹏辉, 葛聪聪, 等. 用于拓展光源的发光二极管反光杯的设计[J]. 唐山师范学院学报,2019,41(6):47-50. doi: 10.3969/j.issn.1009-9115.2019.06.012 FAN Dongxin, LIU Penghui, GE Congcong, et al. Design of a light-emitting diode reflective cup for expanding the light source[J]. Journal of Tangshan Teachers College,2019,41(6):47-50. doi: 10.3969/j.issn.1009-9115.2019.06.012
[13] 郭敬, 张玉杰. 基于遗传模拟退火算法的室内照明节能控制方法研究[J]. 应用光学,2022,43(5):879-885. doi: 10.5768/JAO202243.0502001 GUO Jing, ZHANG Yujie. Research on the energy-saving control method of indoor lighting based on genetic simulation annealing algorithm[J]. Journal of Applied Optics,2022,43(5):879-885. doi: 10.5768/JAO202243.0502001
[14] 王海洋, 金志樑, 王沛沛, 等. 用于LED准直的TIR透镜与反光杯效果研究[J]. 激光与光电子学进展,2021,58(19):320-325. WANG Haiyang, JIN Zhiliang, WANG Peipei, et al. Effect study of TIR lens and reflective glasses for LED collimation[J]. Laser & Optoelectronics Progress,2021,58(19):320-325.
[15] 唐文婷, 张瑞, 陈宝瑨, 等. 一次透镜封装的单片集成LED光源[J]. 应用光学,2022,43(1):137-143. doi: 10.5768/JAO202243.0105003 TANG Wenting, ZHANG Rui, CHEN Baojin, et al. Single lens integrated integrated LED light source[J]. Journal of Applied Optics,2022,43(1):137-143. doi: 10.5768/JAO202243.0105003
[16] ZHANG Q F, GAO J, CHEN X. Simulation and optimization of reflection optical module design for single LED[J]. Optical and Quantum Electronics,2013,45(11):1179-1188. doi: 10.1007/s11082-013-9734-9
[17] 余桂英, 金骥, 倪晓武, 等. 基于光学扩展量的LED均匀照明反射器的设计[J]. 光学学报,2009,29(8):2297-2301. doi: 10.3788/AOS20092908.2297 YU Guiying, JIN Ji, NI Xiaowu, et al. Design of an LED uniform illumination reflector based on the optical extension volume[J]. Acta Optica Sinica,2009,29(8):2297-2301. doi: 10.3788/AOS20092908.2297
[18] CAICEDO D, PANDHARIPANDE A, LEUS G. Occupancy-based illumination control of LED lighting systems[J]. Lighting Research & Technology,2011,43(2):217-234.
[19] ZHANG Q F, GAO J, CHEN X, et al. Simulation and optimization of lens design for single light emitting diode[J]. Sensor Letters,2013,11(2):342-347. doi: 10.1166/sl.2013.2755
[20] 卓宁泽, 张寅, 赵宝洲, 等. LED集成封装的一次光学设计与优化[J]. 光电工程,2013,40(3):129-134. ZHUO Ningze, ZHANG Yin, ZHAO Baozhou, et al. Primary optical design and optimization of the LED integrated package[J]. Photo-Electronic Engineering,2013,40(3):129-134.
[21] MORENO I, AVENDANO-ALEJO M, TZONCHEV R I. Designing light-emitting diode arrays for uniform near-field irradiance[J]. Applied Optics,2006,45(10):2265-2272. doi: 10.1364/AO.45.002265
[22] LUO X, LIU H, LU Z, et al. Automated optimization of an aspheric light-emitting diode lens for uniform illumination[J]. Applied Optics,2011,50(20):3412. doi: 10.1364/AO.50.003412
[23] 周镇, 苏成悦, 付倩, 等. 一种基于自由曲面的LED准直透镜设计[J]. 应用光学,2012,33(6):1058-1062. ZHOU Zhen, SU Chengyue, FU Qian, et al. An LED collimation lens design based on a free surface[J]. Journal of Applied Optics,2012,33(6):1058-1062.
[24] SUN J, ZHANG J W. Design of LED light source for uniform illumination in large area[J]. Applied Mechanics and Materials,2013,401/402/403:465-468.
[25] MORENO I, TZONCHEV R I. Effects on illumination uniformity due to dilution on arrays of LEDs[C]. Bellingham WA: SPIE, 2004.




 下载:
下载:















































































































































 陕公网安备 61011302001501号
陕公网安备 61011302001501号 