Research on three-dimensional face measurement and segmentation system
-
摘要: 三维人脸的测量与分割有着广泛的应用需求,是目前重要的研究方向,但三维人脸数据的庞大、无序等问题制约了其快速发展。首先开发了基于结构光方法的三维人脸测量系统,获得以点云形式存储的高精度三维人脸数据。其次,采用保角变换对三维人脸数据进行了预处理,并采用二维卷积神经网络分割结合三维反映射的思路,实现了三维人脸的分割,解决了三维数据的无序性以及旋转性,降低了三维数据分割的时间消耗。实验结果表明,本文提出的三维人脸测量系统精度可达0.5 mm,三维分割的平均交并比可达0.78,二维分割结合三维反映射的整体效率明显高于直接进行三维分割的效率。Abstract: The three-dimensional face measurement and segmentation have extensive application requirements and are the important research direction at present. However, the rapid development is constrained as the three-dimensional face data is huge and unordered. Firstly, the three-dimensional face measurement system based on the structured light method was developed, and the three-dimensional face data with high precision saved in the form of point cloud was obtained. Secondly, after the conformal transformation was adopted to preprocess the three-dimensional face data and the two-dimensional convolutional neural network segmentation combined with the three-dimensional inverse mapping was adopted, the three-dimensional face segmentation was realized, the disorder and rotation of three-dimensional data were solved, and the time consumption of three-dimensional data segmentation was reduced. The experimental results show that the proposed precision of three-dimensional face measurement system can reach to 0.5 mm, and the average intersection-over-union (IoU) of three-dimensional segmentation can reach to 0.78. The overall efficiency of two-dimensional segmentation combined with the three-dimensional inverse mapping is obviously higher than that of the three-dimensional segmentation.
-
引言
人脸是现代身份识别技术的主要检测特征之一,在档案管理、安全认证、身份记录中有着广泛的应用。与指纹、血型、虹膜等生物特征不同,捕捉人脸不需要与用户接触以及保持其专注和稳定,因而样本的采集较其他生物特征更加安全与便捷[1]。二维人脸分割与识别已得到广泛、深入的研究,大量研究成果已成功实现转化。三维人脸测量、分割与识别是目前的热点研究问题。
人脸区域分割是指结合人脸信息,将人脸区域分割为不同语义标注的部分。除生物识别外,人脸区域分割在动画人脸设计与合成、皮肤美化与虚拟化妆、年龄性别等高等级特征预测等方面均有较多应用[2]。虽然对于人脸的二维图像分割研究已较为成熟,但二维人脸缺少深度,无法表达完整的人脸信息,像素级分割的准确性仍依赖于人脸姿态、光照等条件。随着计算成像的快速发展,已有多种成像方法用于三维人脸成像,如飞行时间(TOF)法[3-6]、激光扫描法等[6]。飞行时间法是通过激光光源发射脉冲信号到物体表面后按原路径返回,由接收器接收,通过激光的传播时间可以计算得到期望的三维信息[5]。但现有曝光算法对飞行时间测距精度和测量范围影响较大[4-6]。激光扫描法基于立体视觉原理,通过投射激光条纹以及使用相机同步记录反射条纹的形状,计算对应点的深度信息来完成三维测量,但激光设备成本较高,测量速度受限[6]。本文采用基于结构光的三维测量方法,具体采用多频外差结合四步相移正弦结构光的方法,实现三维人脸测量。
相较于二维图像,三维人脸数据中包含的几何信息对光照和姿态不敏感[7-8],其包含更多人脸区域分割所需的信息。2017年,Charles等人提出了直接输入点云进行分割的深度学习网络Pointnet[9]。该网络在每个点上独立学习,解决了三维点云输入的无序性以及旋转性这2个关键问题,但其忽略了局部结构。随后Charles等人提出Pointnet++解决了局部结构问题[10]。2018年,Su等人提出了SPLATNet(sparse lattice networks),将输入点云映射到稀疏晶格上,同样解决了三维数据的无序性和旋转性问题[11]。总体而言,由于三维数据的特殊性,为实现三维数据的分割,通常将三维分割模型设计为多边形网格形式,用于保存三维数据的点云与面片信息。在实际应用时,需要在三维分割网络结构、参数量和性能之间进行折衷。
针对三维人脸分割问题,本文开发了一种基于结构光的三维人脸测量系统,实现了人脸的三维采集,其数据以点云形式存储。进一步地,首先采用保角变换将三维人脸数据预处理为二维数据,然后研究了二维卷积神经网络实现了人脸分割,最后将分割后的结果反映射回三维空间,实现了二维映射-二维网络分割-三维逆映射的三维人脸分割方案。
1 三维人脸测量系统
本文开发的三维人脸测量系统由2台相机与1台商用投影仪组成,如图1所示。
对人脸的三维测量采用多频外差结合4步相移正弦结构光的方法,系统标定采用张正友标定法[12]。
1.1 三维人脸测量系统标定
依据张正友标定法,本文将相机的成像过程表述为
$${Z_c}\left[\!\! \begin{gathered} u \\ v \\ 1 \\ \end{gathered} \!\!\right] = \left[\!\! \begin{gathered} \begin{array}{*{20}{c}} {\dfrac{1}{{{\rm{d}}x}}}&0&{{u_0}} \end{array} \\ \begin{array}{*{20}{c}} 0&{\dfrac{1}{{{\rm{d}}y}}}&{{v_0}} \end{array} \\ \begin{array}{*{20}{c}} 0&0&1 \end{array} \\ \end{gathered} \!\!\right]\left[\!\! {\begin{array}{*{20}{c}} f&0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \end{array}} \!\!\right]\left[\!\! {\begin{array}{*{20}{c}} R&t \\ 0&1 \end{array}} \!\!\right]\left[\!\! \begin{gathered} {X_w} \\ {Y_w} \\ {Z_w} \\ 1 \\ \end{gathered} \!\!\right]$$ (1) 式中:
$({X_W},{Y_W},{Z_W})$ 为待测人脸在世界坐标系下的坐标;$(u,v)$ 是待测人脸在相机成像平面投影的像素坐标;${\rm{d}}x {\text{、}}{\rm{d}}y$ 是像素的物理尺寸;$({u_0},{v_0})$ 是相机中心点在成像平面上的像素坐标;$f$ 是相机的焦距;$R {\text{、}}t$ 是世界坐标系到相机坐标系的3×3旋转矩阵和3×1平移矩阵;${Z_c}$ 是待测人脸在相机坐标系下的$Z$ 坐标。忽略相机的切向畸变,在(1)式所示的成像模型中引入径向畸变校正,如(2)式所示:$$\left\{ \begin{array}{l} x' = D(x,y) = (1 + {k_1}{r^2} + \cdots + {k_n}{r^{2n}})x \\ y' = D(y,x) = (1 + {k_1}{r^2} + \cdots + {k_n}{r^{2n}})y \\ \end{array} \right.$$ (2) 式中:
${k_1} ,\cdots, {k_n}$ 是径向畸变系数;$(x',y')$ 是实际像平面坐标;$(x,y)$ 是理想像平面坐标;$r$ 是理想像平面坐标到相机中心像平面坐标的距离。相机参数可采用张正友标定法计算[12]。根据光线可逆原理,投影仪可视为反向相机,辅以完成标定的相机,可以实现投影仪的标定[13-14]。最后,根据对极几何原理,实现相机与投影仪的联合标定[15-16]。1.2 三维人脸测量算法
三维人脸测量的关键在于空间中匹配待测点在左右相机中的成像像素点。本文采用多频外差结合4步相移正弦结构光的方法实现上述目标,4步相移正弦结构光如(3)式所示:
$${I_{{i}}}(x,y) \!=\! {I_0}(x,y) + I(x,y) \cdot \cos (\phi (x,y) + \frac{{\text{π}} }{2}(i - 1)),i \!=\! 1,2,3,4$$ (3) 式中:
${I_0}(x,y)$ 是平均背景灰度值;$I(x,y)$ 是正弦条纹幅值;$\phi (x,y)$ 是相对相位;${I_i}(x,y)$ 是第$i$ 次投影图像$(x,y)$ 处的灰度值。4步相移法求解得到的表征人脸三维数据的相对相位,不具有全局唯一性性质。本文采用三频外差法求解具有全局唯一性性质的绝对相位。三频外差法通过对3个频率的正弦结构光图像进行两两相位展开,得到频率更低的相位图像。本文选择的3个正弦结构光的周期分别为$${\lambda _1} = \frac{1}{{36}},{\lambda _2} = \frac{1}{{30}},{\lambda _3} = \frac{1}{{25}}$$ (4) 采用制造精度为5 μm的标定板对本系统进行评价,本系统三维测量精度为0.5 mm。图2为采用本系统进行三维人脸测量的过程。图2(a)为一幅光栅图像,光栅频率为36;图2(b)与2(c)分别为相对相位与绝对相位图,绝对相位采用三频外差法求得[15];图2(d)为三维人脸测量结果,因受遮挡等影响,测量结果中存在一定的孔洞,本文采用孔洞填充算法进行修补[17]。
2 三维人脸分割算法
为解决三维分割网络的复杂性问题,本文采用了迂回策略,即首先采用保角变换将三维人脸数据映射为二维数据,然后采用二维卷积神经网络实现二维人脸分割,最后将二维分割后的结果逆映射回三维人脸。
2.1 基于保角变换的二维人脸数据映射
在欧式空间中,人脸可视为由多个三维点连接而成的曲面,不具有体积。从微分几何与拓扑学角度出发,若一个三维人脸数据等同于一个亏格为零的曲面,则可映射到一个拓扑球面。Gu等人证明了拓扑球面可以采用保角变换无损地映射到一个拓扑圆盘上[18],即从欧式空间的三维曲面到二维平面的映射。
根据保角结构的概念,保角参数化就是将曲面上局部区域映射到复平面上。若采用
$\omega + {\sqrt { - 1} ^*}\omega $ 定义梯度场,采用$\left\{ {{e_1},{e_2}, \cdots ,{e_{2g}}} \right\}$ 表示一组闭合曲线,可由这组曲线连续变换成曲面上所有闭合曲线,求出曲面的同调基,即可将此曲面沿着同调基切割到一个拓扑圆盘。对曲面与曲面上的一个三角面片$[u,v,w]$ ,可用Munkres提出的方法计算同调基[18],再将三角面片$[u,v,w]$ 的闭合方程写作:$$\omega (\partial [u,v,w]) = \omega [u,v] + \omega [v,w] + \omega [w,u] = 0$$ (5) 而对于曲面上的顶点,其梯度场的Laplacian-Beltrami算子均为0,调和方程表示为
$$\Delta \omega (u) = \sum\limits_{[u,v] \in M} {{k_{u,v}}} \omega [u,v] = 0$$ (6) 设
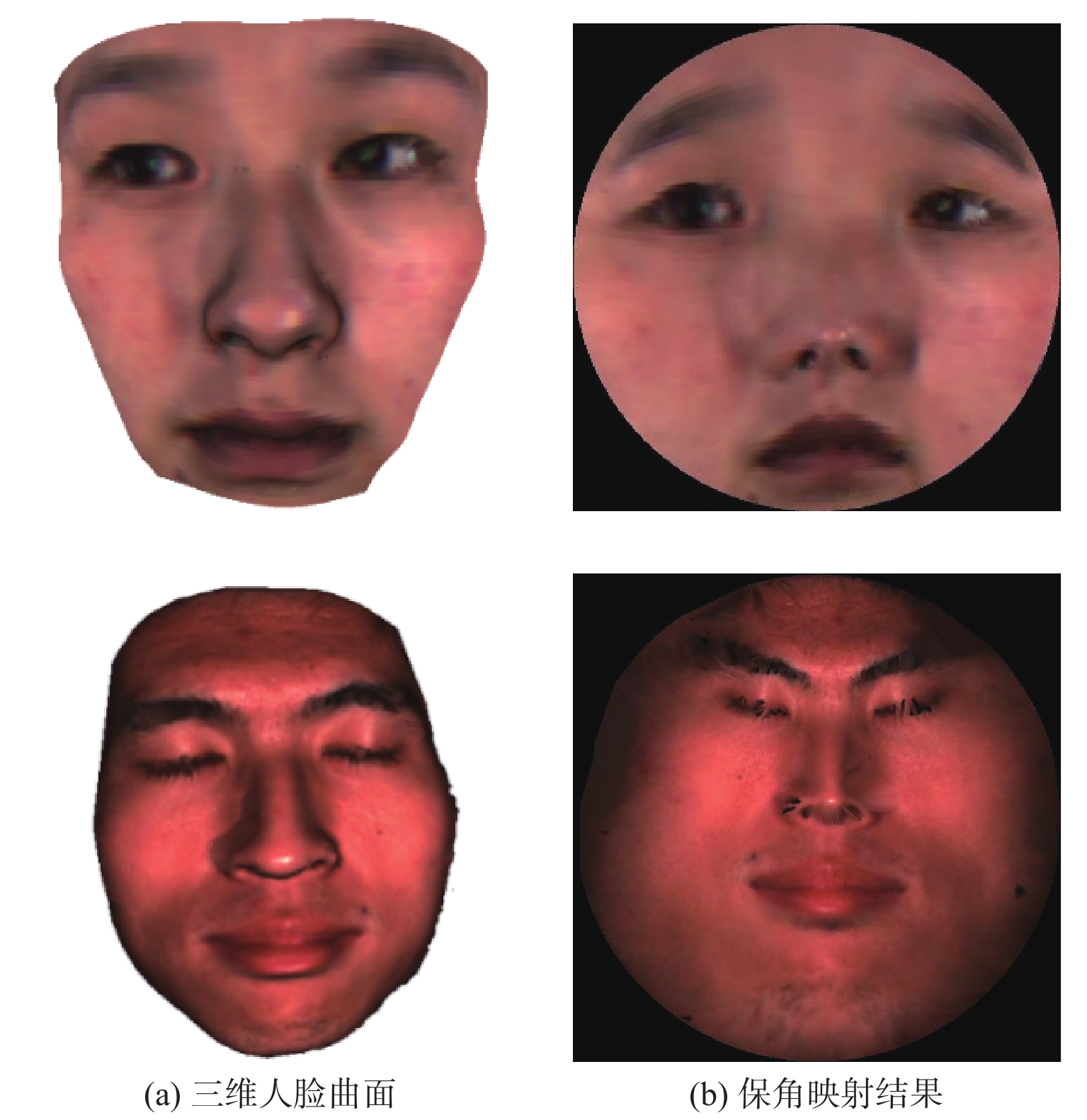
${k_{u,v}}$ 是每条边的权值,若$\alpha $ 与$\beta $ 是对边的角,则有:$${k_{u,v}} = - \frac{1}{2}(\cot \alpha + \cot \beta )$$ (7) 求解(5)~(7)式可得闭合曲面上三维点的参数化坐标。曲面是由离散三维点构成的多个三角面片,这个曲面是不可微的,但可用有限元分段线性函数逼近(等价于用有限元法解Riemann-Cauchy方程)[19]。解得后,可用离散Hodge算子求解保角梯度场,即实现在一个曲面上求解保角映射[20]。从人脸区域分割的角度出发,保角变换可以保证映射到二维平面后,人脸曲面上的任意两条曲线的交角不变[21]。此外,保角变换不受曲面旋转、平移的影响,对不同姿态的同一人脸曲面,其二维映射图像中的人脸特征是一致的。因此,保角变换在人脸各个区域保留了其三维特征。如图3所示,为零亏格人脸曲面参数化后的二维平面域的保角变换结果。本文采用深度学习的方法实现人脸分割,为获得足够的数据量,使用了与本文三维测量系统输出数据格式相同的BJUT三维人脸数据库[22],图3上方三维人脸数据来源于BJUT数据库,下方数据来源于本文系统。
2.2 基于二维CNN的人脸区域分割
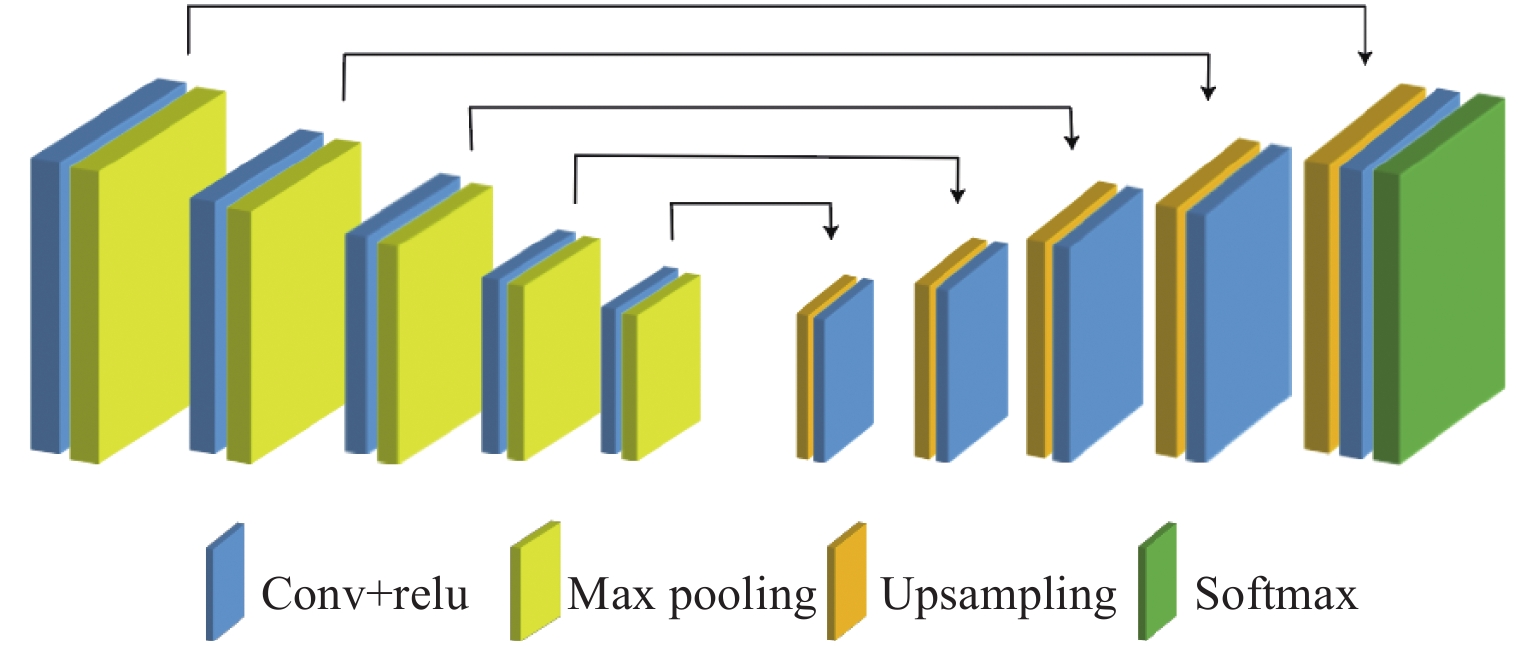
区别于直接对三维人脸区域进行分割,本文对经保角变换后的二维人脸映射图像进行分割研究。采用encoder-decoder结构的卷积神经网络来对二维人脸映射图像进行区域分割,具体架构如图4所示。
其中,编码网络由5个卷积层组成,每一个编码器层对应一个解码器层,因此解码器也有5层。编码网络采用卷积加激活以及最大池化(Conv+ReLU+Maxpooling)的结构,编码器对二维人脸映射图像进行卷积产生特征图,部分结果见图5。激活层采用ReLU函数,最大池化层用于实现图像在小空间内的平移不变性,取局部区域中最大值作为该区域的像素值。解码网络采用卷积加上采样(Conv+Upsampling)的结构。解码器将前面编码得到的抽象特征作为输入,逐层上采样恢复为与输入等大小的图像。在解码器将下采样数据恢复时,特征的大小会发生变化,此时必定会产生信息的丢失,本文在网络中加入Ronneberger等人提出的特征融合步骤,在利用浅层的特征时对其进行裁剪,同时使用跳级连接保证上采样恢复的图像特征边缘更加精细[23]。Lu等人通过实验证明了这种跳级结构能使网络对新的数据敏感度降低,提高边缘特征的精细程度[24]。上采样后,本文采用Softmax层对逐个像素求其分割结果,完成二维人脸映射图像的分割,分割结果采用(8)式表示。
$${p_k}({{x}}) = \exp \left( {{a_k}({{x}})} \right)\Bigg/\left( {\sum\limits_{{k^\prime } = 1}^K {\exp } \left( {{a_k}({{x}})} \right)} \right)$$ (8) 式中:
$K$ 是像素分割类别的总数;${p_k}({{{{x}}}})$ 是第k类中像素点${{x}}$ 的分割结果;$a_k ({{x}}) $ 表示在位置${{{{x}}}}$ 处的像素在特征图中第k层的激活值。网络训练中,采用交叉熵作为损失函数,衡量二维人脸映射图像分割结果,如(9)式所示:$$L = - \sum\limits_{i = 1}^n {{y_i}} \log \left( {{{\hat y}_i}} \right)$$ (9) 式中:
$L$ 表示单张图像的损失函数;${y_i}$ 表示样本属于人脸分割区域中第$i$ 类的概率;${\hat y_i}$ 表示不属于第$i$ 类的概率;$n$ 为总类别数,在本文中$n$ 为2。损失函数值越小则表明网络训练的参数越符合训练集中的样本。2.3 三维逆映射
为得到三维人脸的分割结果,本文采用将二维人脸映射图像的分割结果逆映射到三维人脸曲面的方法。保角变换将人脸区域的三维点、面片映射到拓扑圆盘得到二维人脸映射图像,本文在保角变换中增加了建立索引关系的步骤,即建立三维人脸曲面上的三维点与二维人脸映射图像中二维像素点之间的索引关系,如图6所示。
其中图6(a)为人脸曲面网格,图6(b)为网格上一区域,假设三维人脸曲面上某个三角面片为分割区域,该区域由3个带有纹理信息的三维点构成,映射到二维图像平面上为3个二维坐标点,曲面上每个点都记录了其在保角变换下的二维映射坐标。本文遍历曲面以及映射图像即可将二维分割结果一一逆映射回三维曲面上,从而完成三维人脸区域分割。
3 人脸区域分割结果
对于二维CNN分割网络而言,本文系统测量数据量仍不足以满足训练要求。鉴于本文测量三维人脸数据形式以及纹理信息等与BJUT数据库相同,因此本文二维CNN分割网络的训练、测试使用来自BJUT三维人脸数据库的数据以及系统采集的数据,共505个三维人脸数据。BJUT三维人脸数据库共含500个三维人脸数据,其中男女各250人,年龄分布在16~49岁,表情均为中性,数据包含人脸顶点信息、纹理信息以及网格信息。本文对该数据库的所有人脸数据做预处理。首先对杂散点云以及非人脸部位进行手动去除,保留原曲面点云上点的颜色信息,后采用球旋转算法对人脸点云进行曲面重构,最后使用Netfabb软件进行人工孔洞填充后得到只包含眼睛、眉毛、鼻子、嘴唇这4个部位的零亏格曲面[25]。在本文的三维人脸区域分割研究中,将BJUT数据集中9个噪声较多的人脸三维数据进行了剔除,最终得到了496个零亏格三维人脸曲面及其二维映射图像。本文随机将400幅二维映射图像设置为训练集,63幅设置为测试集。
本文实验的操作系统为Windows10,学习框架为Tensorflow,硬件环境CPU为Intel(R)Xeon(R)E5-2630 2.2 GHz×20,内存256 GB;GPU为Nvidia(R)Tesla P100-PCIE-16 GB×3。本文二维CNN分割网络的平均训练时间为33.1 min,91张测试图像分割总用时小于1 s,单个三维人脸曲面保角变换时间约15 s。本文用准确率
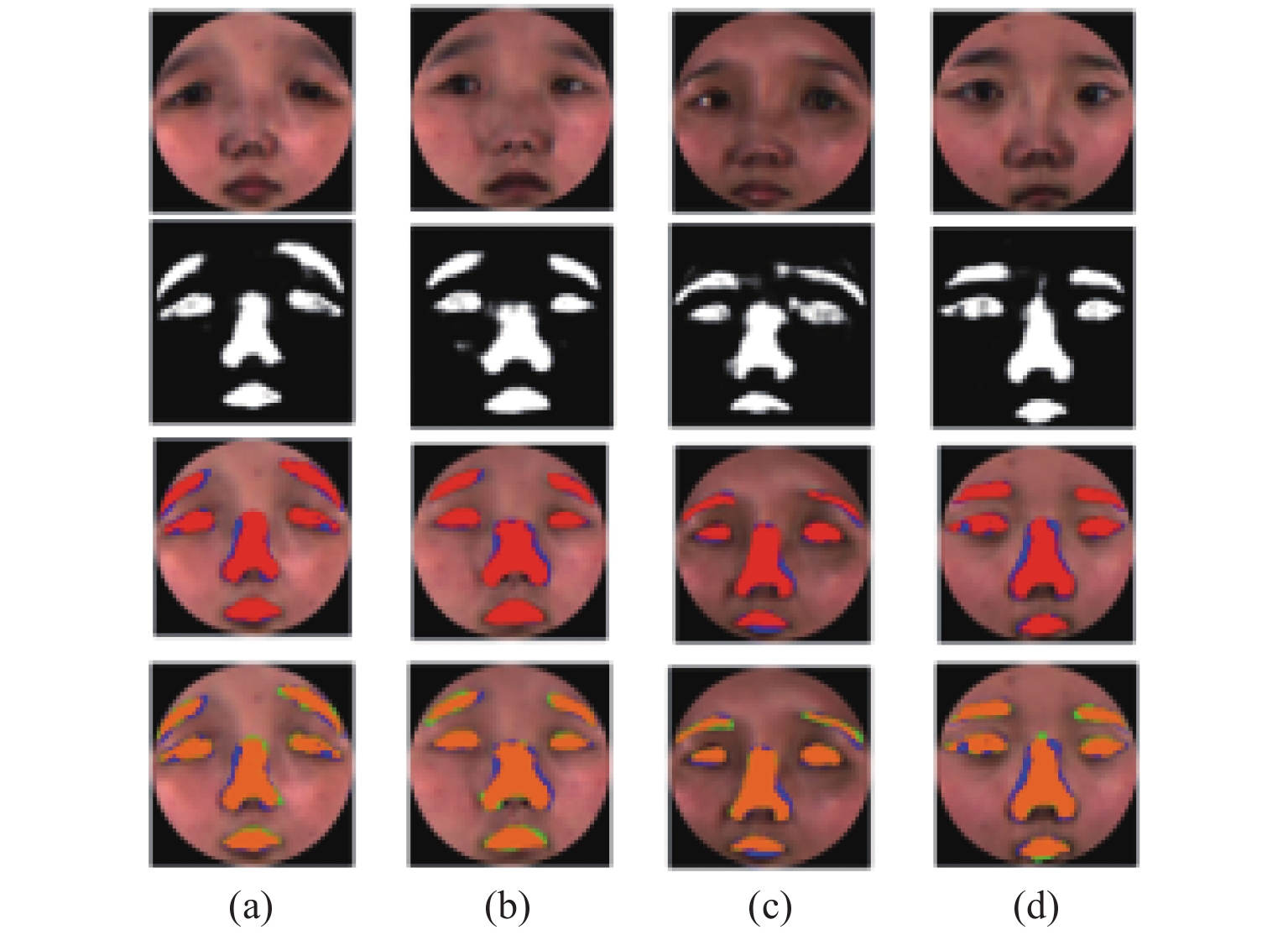
${\rm{P}}$ (precision)和交并比IoU评价二维映射图像分割结果,其中${\rm{TP}}$ (true positive)为真正类,${\rm{FP}}$ (false positive)为假正类,${\rm{TN}}$ (true negatibe)为真负类,${\rm{FN}}$ (false negative)为假负类。$${\rm{P}} = \sum\limits_{}^{} {\frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}}} $$ (10) $${\rm{IoU}} = \sum\limits_{}^{} {\frac{{{\rm{TP}}}}{{{\rm{FN}} + {\rm{TP}} + {\rm{FP}}}}} $$ (11) 部分测试集分割结果如图7所示。其中第1行为4个不同人脸的二维映射图像,第2行为相应的二维映射图像分割结果,第3行为分割准确率(红色为预测部分,蓝色为真值),第4行为IoU结果(蓝色为真值,绿色为预测区域,橘色是相交区域)。
将二维映射图像分割结果根据索引关系一一映射回三维人脸曲面,实验结果如图8所示,可见本文方法能够分割三维人脸曲面中的眉毛、眼睛、鼻子与嘴巴区域。
本文使用PointNet进行对比实验。由于各个三维人脸数据包含点数不同,对试验数据进行了固定点采样。对最远点采样和随机采样两种采样方式下的数据进行试验,在训练次数300次时网络准确率与损失值趋向平稳,训练准确率稳定在0.93~0.95,损失值稳定在0.1~0.12,选取此时网络模型用作测试集分割对比。
对比结果如表1所示。本文二维CNN分割网络的平均训练时长为33.1 min,测试集图像平均准确率为0.93,平均IoU为0.78,完成63张二维图像分割的平均时间小于1 s。在同样的硬件环境下,PoinetNet网络训练时长平均为120 min,完成63个三维测试集数据的平均分割时间为220 s,平均准确率为0.90,平均IoU为0.68。
表 1 本文方法与PointNet分割结果对比Table 1. Comparison of proposed method and PointNet segmentation results参数 本文方法 PointNet 训练耗时/min 33.1 120 分割耗时/s < 1 220 准确率(ACC) 0.93 0.90 交并比(IoU) 0.78 0.68 相较三维实验的结果而言,本文方法实验结果准确率以及IoU更高,在网络训练时间以及预测时间上相较三维网络耗费也较少,在数据存储上,三维数据占用的空间相较二维图像较多,由此可见在三维人脸区域分割任务上,本文方法相较直接将三维数据作为输入的三维网络来说更优。
4 结论
本文提出了一种三维人脸测量与分割系统,该系统基于结构光方法实现对人脸的三维测量。考虑到三维分割网络的复杂性,提出了一种二维映射-二维分割-三维逆映射的分割策略。实验结果表明,虽然经过保角变换后的二维人脸在图像上存在视觉变化,但对人脸的区域分割并无影响,本文方法能够采用较为轻简的网络以较高的效率实现人脸区域分割。相较于传统二维人脸的分割方法,提出的三维人脸测量与区域分割系统能获取三维人脸的结构信息,不受光照条件和三维人脸姿态的影响,相较于现有的三维分割方法,本文避免了设计复杂的三维分割网络,有效地降低了在网络上的开发难度。
本文采用基于多频外差结合四步相移正弦光栅的方法实现三维人脸测量,系统采集数据时需要投射12幅正弦光栅,测量所用时间较长。目前已有研究可实现单帧投影的三维测量,后续研究将考虑对系统在此方面进行改进。此外,受限于三维人脸数据的样本数,本文仅进行了三维人脸区域分割的研究,若能进一步增加测量数据量,一方面可以通过研究二维分割网络以提高三维人脸区域分割的准确率,另一方面可以采用本文方法开展基于保角变换与二维识别网络的三维人脸识别研究。
-
表 1 本文方法与PointNet分割结果对比
Table 1 Comparison of proposed method and PointNet segmentation results
参数 本文方法 PointNet 训练耗时/min 33.1 120 分割耗时/s < 1 220 准确率(ACC) 0.93 0.90 交并比(IoU) 0.78 0.68 -
[1] ZHOU S, XIAO S. 3D face recognition: a survey[J]. Human-centric Computing and Information Sciences,2018,8(1):35-62. doi: 10.1186/s13673-018-0157-2
[2] PATIL H, KOTHARI A, BHURCHANDI K. 3-D face recognition: features, databases, algorithms and challenges[J]. Artificial Intelligence Review,2015,44(3):393-441. doi: 10.1007/s10462-015-9431-0
[3] HUSSMANN, HERMANSKI A. Real-time image processing of TOF range images using a single shot image capture algorithm[C]//2012 IEEE I2MTC - International Instrumentation and Measurement Technology Conference. Graz, Austria: IEEE, 2012: 1551-1555.
[4] STEFAN M, DAVID D, DIRK H, et al. Three-dimensional mapping with time-of-flight cameras[J]. Journal of Field Robotics,2009,26(11/12):934-965. doi: 10.1002/rob.20321
[5] 曾少青. 基于飞行时间法原理的三维成像系统设计[D]. 湖南: 湘潭大学, 2017. ZENG Shaoqing. Design of 3D camera system based on time-of-fight principle[D]. Hu’nan: Xiangtan University, 2017.
[6] FUCHS S, HIRZINGER G. Extrinsic and depth calibration of ToF-cameras[C]//2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, AK, USA: IEEE: 1-6.
[7] GUO Y, WAN J, LU M, et al. A parts-based method for articulated target recognition in laser radar data[J]. Optik-International Journal for Light and Electron Optics,2013,124(17):2727-2733.
[8] GUO Y, SOHEL F A, BENNAMOUN M, et al. RoPS: a local feature descriptor for 3D rigid objects based on rotational projection statistics[C]//Proceedings of 2013 1st International Conference on Communications, Signal Processing, and their Applications (ICCSPA). Sharjah: IEEE, 2013: 1-6.
[9] QI C R, SU H, MO K, et al. PointNet: deep learning on point sets for 3d classification and segmentation[C]//Proceedings of Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2016: 77-85.
[10] QI C R, YI L, SU H, et al. PointNet++: deep hierarchical feature learning on point sets in a metric space[C]//Conference and Workshop on Neural Information Processing Systems. Long Beach, NIPS, 2017: 1-14.
[11] SU H, JMAPANI V, SUN D, et al. SPLATNet: sparse lattice networks for point cloud processing[C]//Proceedings of Conference on Computer Vision and Pattern Recognition (CVPR). Salt Lake: IEEE, 2018: 2530-2539.
[12] ZHANG Z. Flexible camera calibration by viewing a plane from unknown orientations[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision. Honolulu: IEEE, 1999: 666-673.
[13] SONG Z, HUANG P S, et al. Novel method for structured light system calibration[J]. Optical Engineering,2006,45(8):083601. doi: 10.1117/1.2336196
[14] 朱勇建, 黄振, 马俊飞, 等. 光栅投影三维测量系统标定技术研究[J]. 应用光学,2020,41(5):68-76. ZHU Yongjian, HUANG ZHEN, MA Junfei, et al. Study on calibration method of grating projection 3D measuring system[J]. Journal of Applied Optics,2020,41(5):68-76.
[15] 达飞鹏, 盖绍彦. 光栅投影三维精密测量[M]. 北京: 科学出版社, 2011: 45-62. DA Feipeng, GAI Shaoyan. Grating projection 3D precision measurement[M]. Beijing: Science Press, 2011: 45-62.
[16] 贺文俊, 王加科, 付跃刚, 等. 基于双目立体视觉的高压绝缘子在线检测系统[J]. 应用光学,2018,39(4):528-535. HE Wenjun, WANG Jiake, FU Yuegang, et al. On-line measurement system of high voltage insulator based on binocular stereo vision[J]. Journal of Applied Optics,2018,39(4):528-535.
[17] JUN Y. A piecewise hole filling algorithm in reverse engineering[J]. Computer-Aided Design,2005,37(2):263-270. doi: 10.1016/j.cad.2004.06.012
[18] GU X, WANG Y, CHAN T F, et al. Genus zero surface conformal mapping and its application to brain surface mapping[J]. IEEE Transactions on Medical Imaging,2004,23(8):949-958. doi: 10.1109/TMI.2004.831226
[19] REDDY J N. An introduction to nonlinear finite element analysis[M]. Oxford: Oxford University Press, 2004: 145-152.
[20] KRA I, FARKAS H M. Riemann surfaces[M]. New York: Springer-Verlag, 1992: 221-239.
[21] GU X, YAU S T. Global conformal surface parameterization[C]//Proceedings of Institute of Electrical and Electronics Engineers Visualization. Austin: IEEE, 2004: 267-274.
[22] 尹宝才, 孙艳丰, 王成章, 等. BJUT-3D三维人脸数据库及其处理技术[J]. 计算机研究与发展,2009,46(6):123-132. YIN Baocai, SUN Yanfeng, WANG Chengzhang, et al. BJUT large scale 3D face database and information processing[J]. Journal of Computer Research and Development,2009,46(6):123-132.
[23] RONNEBERGER O, FISCHER P, BROX T. U-Net: convolutional networks for biomedical image segmentation[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Switzerland: Springer Cham, 2015: 234-241.
[24] LU J, TONG K Y. Visualized insights into the optimization landscape of fully convolutional networks[EB/OL]. [2019-1-20]. https://arxiv.org/abs/1901.08556.
[25] JIANG J F, ZHONG Y Q, ZHANG Q P. Three-dimensional garment surface reconstruction based on ball-pivoting algorithm[J]. Advanced Materials Research,2013(821/822):765-768.
-
期刊类型引用(3)
1. 王坚. 基于修正Gram-Schmidt法的双连通区域数值保角逆变换计算法. 科技风. 2024(17): 161-164 .  百度学术
百度学术
2. 李炜. 基于面部边缘细节的局部遮挡人脸图像识别. 吉林大学学报(信息科学版). 2023(04): 732-738 .  百度学术
百度学术
3. 焦瑾瑾. 光谱匹配技术在人脸轮廓三维图像成像中的应用. 激光杂志. 2022(07): 85-89 .  百度学术
百度学术
其他类型引用(1)




 下载:
下载:
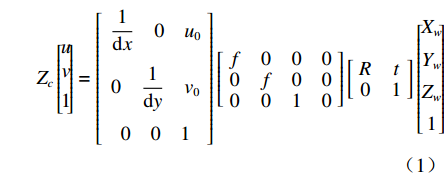
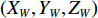
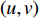
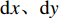
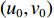
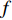
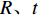
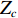
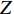
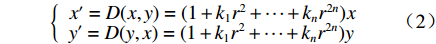
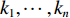
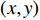
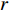
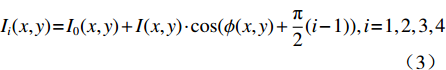
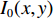
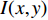
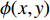
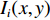
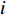
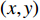
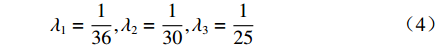

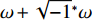
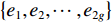
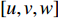
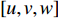
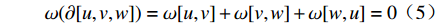
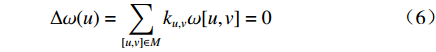

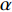
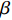
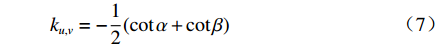

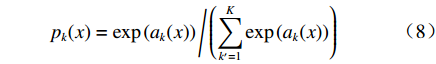
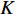
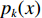
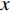
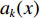
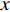
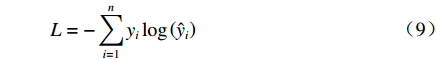
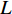
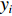
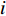
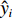
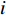
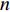
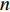

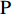



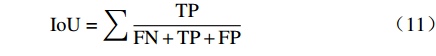

 陕公网安备 61011302001501号
陕公网安备 61011302001501号 