Opto-mechanical assembly and analysis of spectral module in visible-short wave infrared band
-
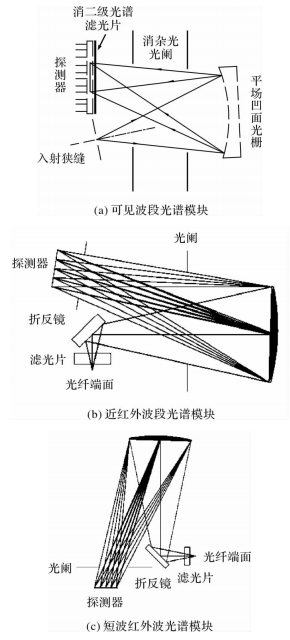
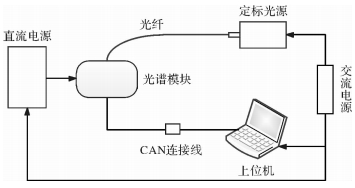
摘要: 介绍了自行研制的辐射仪器的光谱模块,其光谱范围覆盖可见-短波红外波段(400 nm~2 500 nm),讨论了光谱模块的装调方法并对装调结果进行了分析研究。辐射仪器由3个光谱模块组成,分别是可见波段光谱模块(400 nm~1 000 nm),近红外波段光谱模块(900 nm~1 700 nm)和短波红外波段光谱模块(1 600 nm~2 500 nm),光谱模块的探测单元均以平场凹面光栅分光,线阵探测器探测信号,光谱模块的光机组件主要包括光纤头、狭缝、反射镜组件、光栅组件和探测器组件等。鉴于光谱模块的光机装调效果与其光机设计息息相关,装调结果的好坏能反映光机设计的优劣,针对光谱模块的光机设计特点进行了光机装调。光机装调分析结果表明:3个光谱模块的波长分辨率分别优于4 nm,15 nm和20 nm,达到了仪器的设计指标,验证了光机设计、装调的合理性。Abstract: The spectral modules of self developed radiometer are introduced. The spectral range covers the visible-short wave infrared band(400 nm~2 500 nm).The methods of opto-mechanical assembly of spectral modules are discussed and the results of opto-mechanical assembly are analyzed. The radiometer consists of three spectral modules: the visible spectral module(400 nm~1 000 nm)(VIS for short), the near-infrared spectral module(900 nm~1 700 nm)(NIR for short), and the short wave infrared spectral module(1 600 nm~2 500 nm)(SWIR for short).The detection units of spectral module use the flat-field concave grating to diffract and focus different wavelengths, use the linear array detector to detect signals.The optical units of spectral modules consist of optical fiber, slit, assembly of reflector, assembly of grating and assembly of detector. Since the effect of opto-mechanical assembly is closely related to opto-mechanical design, the result of opto-mechanical assembly can reflect the advantages and disadvantages of opto-mechanical design. According to the characteristics of the opto-mechanical design of the spectral modules, the opto-mechanical assembly was carried out. The results of opto-mechanical assembly show that the wavelength resolution of the three spectral modules is better than 4 nm, 15 nm and 20 nm, respectively. The design indexes of the spectral module are achieved, verifying the rationality of the opto-mechanical design.
-
引言
激光测量技术作为一种非接触式高精度测量技术,在工业生产中具有非常重要的应用价值。激光三角测距技术[1]是实现非接触式距离测量的重要手段,该方法可以快速给出目标的位移、厚度、振动、速度等丰富信息[2-6],具有测量速度快、精度高、抗干扰性能强、适用范围广等优点,已广泛应用于工业领域。
现阶段基于激光三角测量的位移传感器,大多用于量程较小的精密位移测量[7-8]。由于激光三角测量的原理限制,想实现中近距离的大量程精确位移测量会不可避免地降低输入输出的线性度、增大横向体积,一些情况下量程两端的灵敏度甚至相差数十倍,线性误差严重。而目前激光三角法测距的结构优化对线性度的研究较少,大多仅针对灵敏度或宽度进行参数或结构优化,如在参数直接对比后选择性能更好的组合[9-11];或对激光三角法的结构进行简化或改进,如在光路中添加分束镜[12-13];亦或直接在透镜后方添加反射镜[14],将像距部分进行折叠,但在中远距离及像距较小的结构中折叠效果有限。为了提高远距离准确性与仪器便携性,增加应用场景,需要合理设计激光三角测量器件的结构参数,在降低器件体积的同时保持优秀的灵敏度与线性度。
本文从理论上对激光三角法原理进行分析研究,分析了主要结构参数对器件性能的影响。同时,为提高激光三角测量的线性度及减小仪器尺寸,在接收光路中设置平面转像反射镜实现光路折叠,并利用引力搜索算法优化了系统结构参数,获得了更高的线性度,为激光三角位移传感器的性能优化提供了一种新的方案。
1 激光三角法原理
激光三角法分为直射式和斜射式两种,直射式激光三角法相比于斜射式具有结构紧凑、光斑均匀、计算简单等优点[1],本文仅针对直射式激光三角法进行讨论。图1所示为直射式激光三角测距的基本原理图。透镜光轴与激光路径形成一定夹角,激光器发出的激光在物体表面形成光斑,经被测表面散射后被透镜成像在光电探测器件中,并且随着被测物面距离的变化,光斑在线阵光电探测器件中所成像的位置也发生变化,两者一一对应。因此传感器在经过标定后,输入输出特性被确定,通过线阵光电器件接受的像素信息就可以得到所测物面的距离,本系统的线阵光电探测器件选用线阵CMOS(互补金属氧化物半导体)。
图1中,y为被测距离;∆x为像点在线阵CMOS上的位移,在图1中取左正右负;∆y为被测面的位移,根据与传感器的距离取远正近负;a为参考面的工作物距;b为与a对应的工作像距;α为激光与透镜光轴的夹角;β为线阵CMOS与透镜光轴的夹角,不宜小于30°,否则会降低线阵CMOS的接收性能,也会导致像斑的强度中心和形状中心偏移较大,从而影响光斑定位;d为透镜光轴与线阵CMOS交点到其左边缘的距离。
由透镜的成像原理可推出,要使每一个光斑都在线阵CMOS上呈清晰的像点,激光三角测量系统必须满足Scheimpflug条件[1],即透镜主面、激光和线阵CMOS的延长线交于一点。由图1中的图像关系可得:
$$ a\tan \alpha = b\tan \beta $$ (1) 根据结构关系及透镜成像原理,可得物面位移∆y与线阵CMOS上像斑位移∆x的关系:
$$ \Delta y = \frac{{a\Delta x\sin \beta }}{{b\sin \alpha - \Delta x\sin (\alpha + \beta )}} $$ (2) $$ \Delta x = \frac{{b\Delta y\sin \alpha }}{{a\sin \beta + \Delta y\sin (\alpha + \beta )}} $$ (3) 则该位移传感器在∆y位置的灵敏度为
$$ S = \frac{{\partial x}}{{\partial y}} = \frac{{ab\sin \alpha \sin \beta }}{{{{[a\sin \beta + \Delta y\sin (\alpha + \beta )]}^2}}} $$ (4) 最远量程处的灵敏度为整个仪器的最小灵敏度,可用以表征整个仪器的性能。对于参数a=300 mm,α=π/6,f=25 mm且∆x= −4 mm~4 mm的激光三角位移传感器,当只改变a、α或f中的其中一种参数时,该参数与器件最大量程处的灵敏度Smin及量程R的关系如图2~图4所示。
由图2~图4可知,成像系统的工作物距a越小、夹角α和透镜焦距f越大,器件的最小灵敏度Smin越大,测量范围越小。在激光三角系统中,灵敏度主要取决于透镜成像的垂轴放大率$ \eta=\dfrac{b}{a} $与夹角α[15]。根据透镜成像牛顿公式,a减小及f增大都使得垂轴放大率η增大,x相对y的移动会越明显;角度α越大,系统的探测范围越小,灵敏度会越高,但光斑的散射光强度会随之降低。因此,为了取得较亮的光斑图像,一般将α约束在40°以内。
线性度也是传感器静态特性的重要指标之一,表示传感器输入输出曲线与理想直线的符合程度,良好的线性度可以使器件输出分析更加方便,从而提高测量的精确度[16]。对于激光三角位移传感器来说,若近距离处与远距离处灵敏度的倍数差异过大,那么后续光斑定位等步骤也会造成相应倍数的误差,这对传感器远距离测量精度的影响是不可忽视的。激光三角位移传感器的线性度主要与夹角α有关,假设在极端条件下激光完全与透镜光轴垂直,即α=90°,则在理想成像条件下垂轴放大率恒定,输入输出完全呈直线关系,此时灵敏度S等于垂轴放大率η。随着夹角α减小,近轴与量程两端的成像放大率差异增大,特别对于量程较大的测量条件,器件量程最远与最近处在透镜平面的物距差异较大,线性度也因此急剧劣化,所以激光三角的夹角一般不小于20°且多用于量程较小的测量环境。对于确定的量程与线阵传感器件成像宽度,灵敏度S对线阵探测元件的成像长度x积分总和是一定的。因此,最小灵敏度Smin较大的结构,在总量程内的灵敏度分布更平均,线性度更佳。
2 改进结构分析
如图5所示,在透镜与被测面中间某一位置放置一块平面反射镜以折叠光路,使反光镜、透镜、线阵CMOS及激光器排列在同一横向范围内,可进一步提高器件内部空间的利用率,减小器件体积。设反射镜与透镜的距离为c,由图像分析可知,c的取值越大,对器件宽度的减小越明显;同时c的存在也会使测量距离y被折叠,从而使测量距离比未折叠前缩短$ c \cos \alpha $,器件量程的近端与远端的物距均增长$ c \cos ^{2} \alpha $。由透镜成像原理可得两端灵敏度差异会减小,但为了保持量程范围不变,需相应增大透镜焦距。
选用线阵CMOS的可成像区域长度为8 mm,则∆x的范围为(d-8, d),整个系统的其他参数都可由a、α、c、f、d来确定,由透镜成像的牛顿公式可得:
$$ \frac{1}{a}+\frac{1}{b}=\frac{1}{f} $$ (5) 参考平面距离为
$$ y=(a-c) \cos \alpha $$ (6) 器件宽度w为
$$ w=(a-c) \sin \alpha $$ (7) 反射镜距线阵CMOS的距离为(b+c),因此得到条件:
$$ b+c \leqslant(a-c) \sin \alpha $$ (8) 器件的最大量程和最小量程分别为
$$ y_{\max }=y+\Delta y_{\max }=y+\frac{a d \sin \beta}{b \sin \alpha-d \sin (\alpha+\beta)}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; $$ (9) $$ y_{\min }=y+\Delta y_{\min }=y+\frac{a(d-8) \sin \beta}{b \sin \alpha-(d-8) \sin (\alpha+\beta)} \;\;\;\;\;\;\;$$ (10) 夹角α对线性度的影响最大[15],但夹角过大会降低接收的散射光强度并增大反射镜长度而凸出仪器,因此直接取α=40°。以a、c、d、f为优化量并合理设定取值范围,联立式(1)~式(10)后建立约束条件:
$$ \left\{\begin{array}{l} 100 \leqslant a \leqslant 800 \\ 0 \leqslant c \leqslant \dfrac{a \sin \alpha-b}{1+\sin \alpha} \\ -2 \leqslant d \leqslant 10 \\ 6 \leqslant f \leqslant 50 \\ \alpha=40^{\circ} \\ y_{\max } \geqslant 500 \\ y_{\min } \leqslant 200 \\ (a-c) \sin \alpha \leqslant 200 \end{array}\right. $$ (11) 3 算法优化过程
3.1 引力搜索算法(GSA)
引力搜索算法[17]是由伊朗的克曼大学教授RASHEDI E等学者提出的一种智能优化算法,该算法将搜索粒子看作一组在n维空间运行的物体,物体间通过万有引力相互作用吸引,适度值较大的粒子惯性质量越大,因此万有引力会促使物体们朝着质量最大的物体移动,从而逐渐逼近最优解。引力搜索算法具有较强的全局搜索能力与较快的收敛速度,很多学者也对其进行改进,进一步增强了其优化能力[18-20]。
算法首先随机生成N个n维初始粒子,设第i个粒子的坐标为Xi={xi1, xi2, …, xim, …, xin},其中xim表示第i个粒子在第m维空间中的坐标。则在t时刻或第t次迭代时,任意第j个粒子对第i个粒子在第m维的吸引力定义为
$$ {F_{ij}}^m(t) = G(t)\frac{{{M_i}(t){M_j}(t)}}{{{R_{ij}}(t) + r}}\left[ {x_j^m(t) - x_i^m(t)} \right] $$ (12) 实验证明,直接用欧氏距离Rij(t)+r代替原引力公式中的距离平方Rij2(t),可以取得更好的效果[17],其中r为一个很小的常数,防止分母为0。G(t)为t时刻的万有引力常数,随宇宙年龄的增加而减少,一般表示为$G(t)=G_0\exp(-\mathrm{\mathit{k}}t/{{{T}}})$。改变式中k的大小,可调整算法的收敛速度,k的值越大,随着算法迭代G(t)值减小的速度越慢。[xjm(t)−xim(t)]用来表征第m维度引力分量的比例大小。粒子质量Mi(t)与粒子的适应度有关,粒子适应度越大,粒子质量就越大,对其他粒子的吸引力就越强。粒子质量Mi(t)的计算公式为
$$ m_{i}(t)=\frac{f_{i}(t)-w(t)}{b(t)-w(t)} $$ (13) $$ M_{i}(t)=\frac{m_{i}(t)}{\displaystyle\sum\limits_{k=1}^{N} m_{k}(t)} $$ (14) 式中:fi(t)为t时刻第i个粒子的适应度,b(t)和w(t)分别为t时刻所有粒子中最好和最差的适应度。根据式(12)~式(14)得到每个粒子在各维度受其他粒子的合力,以及牛顿第二定律加速度$ a_{i}=F_{i} / M_{i} $,即可求得本次迭代的粒子加速度并更新粒子速度与位置。引力搜索算法的具体流程如图6所示,在达到停止条件前循环迭代,不断更新粒子信息,直到达到停止迭代条件。
3.2 优化参数分析
以a、c、d、f为优化量,分别对应于章节3.1中粒子的xi1、xi2、xi3、xi4这4个纬度坐标进行优化。此器件的优化目标是在限制器件宽度的情况下,取得更好的线性度,因此目标函数设定为最小值问题:
$$ \min f(x)=\frac{S_{\max }}{S_{\min }} $$ 式中:Smax为式(4)中测量距离最近处的灵敏度;Smin为测量距离最远处的灵敏度。根据章节1分析,量程越大或宽度越小,量程两端的灵敏度差距会越明显,因此算法会将量程逐渐逼近200 mm~500 mm,宽度逼近200 mm。根据引力搜索算法原理,编写python算法程序,设定章节3.1中初始引力常数G0=20,r=1,k=10,迭代次数为50次,初始随机粒子数为200。
本模型中有较多不等式约束,对于函数的不等式约束,使用罚函数法在目标函数中添加障碍函数使约束问题转化为无约束问题。本文采用罚函数法中的内点障碍函数法,该方法可在解空间边界筑起高墙,粒子靠近边界时会使函数值陡然增大。基于此方法,在程序中生成初始随机粒子时,检测是否符合约束条件,若不符合则重新生成。
3.3 优化结果
对迭代过程中的最佳粒子位置进行跟踪记录,每次迭代后其各维度参数及目标函数结果如图7和图8所示,各参数变量随着迭代次数的增加逐渐趋于稳定,获得所需的最佳结构参数,目标Smax/Smin值随着迭代逐步降低,表征该系统的线性度逐步提高。
参数优化结果如表1所示。
表 1 算法优化后的结构参数Table 1. Structural parameters optimized by the algorithmSmax/Smin a/mm α/(°) c/mm d/mm f/mm w/mm Smax Smin 2.357 484.19 40 173.04 6.53 25.54 200 0.040 9 0.017 4 一般激光三角法直接采用经验及一定计算来选定参数。作为对比参照,同样利用经验法确定透镜焦距f=25 mm,光轴经过线阵CMOS中间即d=4 mm,则利用量程200 mm~500 mm,宽度w=200 mm这3个约束可计算得a、α、c值。未经过算法优化的结构参数如表2所示。
表 2 未经过算法优化的结构参数Table 2. Unoptimized structural parametersSmax/Smin a/mm α/(°) c/mm d/mm f/mm w/mm Smax Smin 2.769 500.44 32.61 129.33 4 25 200 0.044 4 0.016 0 而对于非折叠激光三角结构,在相同的200 mm~500 mm量程、宽度200 mm约束下采用引力搜索算法优化其结构,以a、d、f 为优化量,计算非折叠结构的最佳参数,可优化得其参数如表3所示。
表 3 优化后的非折叠结构参数Table 3. Optimized non-folding structure parametersSmax/Smin a/mm α/(°) d/mm f/mm w/mm Smax Smin 3.62 291.12 40 6.91 18.74 200 0.050 7 0.014 0 3种结构的灵敏度与输入输出曲线如图9所示。
由表1~表3可知,在宽度相同的情况下都分别优化出最佳参数,本文参数结构与未优化的同结构相比,500 mm处的灵敏度提高了8.75%;与非折叠结构相比,500 mm处的灵敏度提高了24.29%。由图9可见,本文优化结构的量程两端灵敏度差异较小,在量程范围内的灵敏度分布更加平均,输出更接近直线。采用最小二乘法对输入输出曲线进行直线拟合,本文优化结构的非线性误差为7.43%,均方误差为9.56;未优化参数结构的非线性误差为8.90%,均方误差为11.34;而非折叠结构的非线性误差为11.40%,均方误差为14.27,线性度较差。
4 结论
本文提出了一种提高激光三角测量线性度的优化方法。在改进结构中将所有器件摆放在同一横向直线上,可以明显减少器件的横纵向宽度并提高线性度,降低远距离测量的误差。比较结果表明,相比于经验法与原非折叠结构,此优化方法有更好的理论依据和优化效果,对激光三角器件的体积与线性度具有多方面正向优化作用,具有现实意义。
本文是对激光三角结构优化的一个环节,所采用的的优化算法同样适用于其他量程或器件选型的结构优化,并可通过修改约束条件来匹配更多应用场景,具有普适性。本结构也有一定不足,所需反射镜的长度与反射镜与成像透镜距离成正比,为使结构紧凑也需对反射镜的长度做出一定约束,同时未来也将对算法的迭代速度等方面进行进一步改进。
-
表 1 可见波段光谱模块谱线中心坐标
Table 1 Center coordinates of spectral line of VIS module
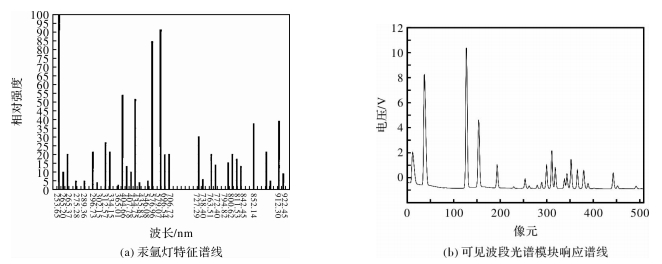
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 波长/nm 404.66 435.84 546.07 696.543 706.722 727.294 738.398 750.387 763.511 772.376 794.818 800.616 811.531 826.452 842.465 852.144 912.297 922.45 中心像元 11.758 5 37.128 4 127.701 9 254.678 8 263.565 1 280.943 2 290.579 5 301.243 2 312.468 9 320.259 7 340.057 6 345.422 0 354.452 1 368.024 5 381.712 4 391.012 2 445.644 1 454.962 9 表 2 可见波段光谱模块半高宽和评估分辨率
Table 2 FWHM and resolution of VIS module
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 波长/nm 404.66 435.84 546.07 696.543 706.722 727.294 738.398 750.387 763.511 772.376 794.818 800.616 811.531 826.452 842.465 852.144 912.297 922.45 半高宽/nm 3.389 6 3.457 5 3.311 6 2.930 3 2.548 8 2.668 0 2.661 8 2.967 1 2.764 1 2.723 6 2.974 6 2.875 3 3.022 9 2.871 7 3.361 0 2.831 1 3.118 2 3.112 1 评估分辨率/nm 3.920 8 3.999 3 3.830 5 3.389 4 2.948 2 3.085 9 3.078 8 3.432 0 3.197 2 3.150 3 3.440 7 3.325 8 3.496 5 3.321 7 3.887 7 3.274 6 3.606 8 3.599 7 表 3 近红外波段光谱模块谱线中心坐标
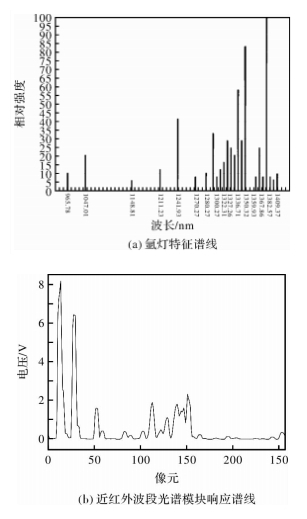
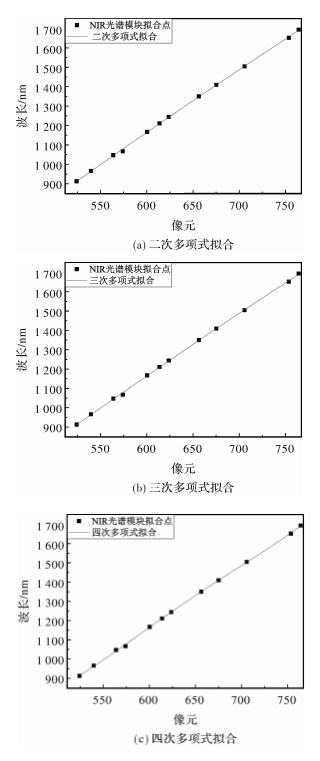
Table 3 Center coordinates of spectral line of NIR module
序号 1 2 3 4 5 6 7 8 9 10 11 12 波长/nm 912.296 7 965.778 6 1 047.005 4 1 067.356 5 1 166.871 1 211.232 6 1 243.932 1 1 350.419 1 1 409.36 1 504.65 1 651.986 1 694.058 中心像元 524.185 0 539.662 4 563.859 0 574.132 6 600.372 9 613.805 6 623.707 8 656.388 3 675.193 6 705.768 7 753.635 0 764.223 9 表 4 近红外波段光谱模块半高宽与评估分辨率
Table 4 FWHM and resolution of NIR module
序号 1 2 3 4 5 6 7 8 9 10 11 12 波长/nm 912.296 7 965.778 6 1 047.005 4 1 067.356 5 1 166.871 1 211.232 6 1 243.932 1 1 350.419 1 1 409.36 1 504.65 1 651.986 1 694.058 半高宽/nm 4.601 4 4.042 4 3.689 4 3.170 6 4.045 6 4.090 2 4.627 0 3.245 0 3.939 0 4.625 2 4.331 6 4.663 0 评估分辨率/nm 14.769 4 12.975 2 11.842 1 10.176 8 12.985 4 13.128 5 14.851 8 10.415 8 12.643 1 14.846 1 13.903 4 14.967 1 表 5 短波红外波段光谱模块谱线中心坐标
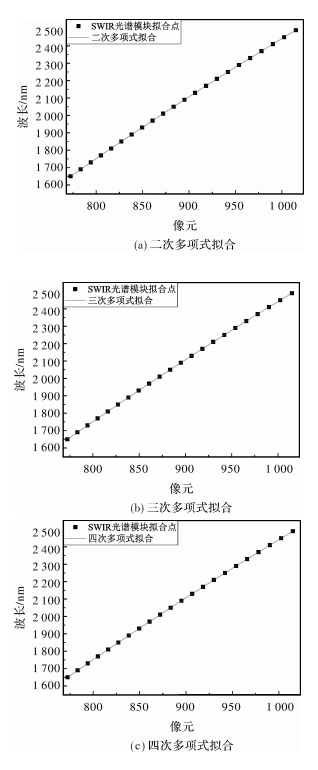
Table 5 Center coordinates of spectral line of SWIR module
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 波长/nm 1 650 1 690 1 730 1 770 1 810 1 850 1 890 1 930 1 970 2 010 2 050 2 090 2 130 2 170 2 210 2 250 2 290 2 330 2 370 2 410 2 450 2 490 中心像元 5.351 16.225 27.121 38.071 49.105 60.133 71.262 82.477 93.71 105.115 116.476 128.014 139.613 151.316 163.009 174.969 186.903 198.868 211.119 223.383 235.513 248.146 表 6 短波红外波段光谱模块半高宽和评估分辨率
Table 6 FWHM and resolution of SWIR module
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 波长/nm 1 650 1 690 1 730 1 770 1 810 1 850 1 890 1 930 1 970 2 010 2 050 2 090 2 130 2 170 2 210 2 250 2 290 2 330 2 370 2 410 2 450 2 490 半高宽/nm 4.578 4.644 4.521 4.56 4.729 4.73 4.602 4.685 4.554 4.658 4.521 4.791 4.753 4.832 4.502 4.79 4.992 5.194 5.425 5.334 4.674 4.735 评估分辨率/nm 15.827 16.056 15.633 15.767 16.35 16.354 15.91 16.198 15.745 16.106 15.631 16.567 16.435 16.708 15.566 16.563 17.259 17.958 18.758 18.442 16.162 16.372 -
[1] CZAPLAMYERS J S, LEISSO N P, ANDERSON N J, et al. On-orbit radiometric calibration of earth-observing sensors using the radiometric calibration test site (RadCaTS)[J]. SPIE, 2012, 8390:83902B-9. http://cn.bing.com/academic/profile?id=2139eb130b6cfaccb7888b9b0a568ee4&encoded=0&v=paper_preview&mkt=zh-cn
[2] 尹亚鹏, 李新, 郑小兵, 等.场地自动化观测辐射计的设计与实现[J].大气与环境光学学报, 2016, 11(1):44-50. http://d.old.wanfangdata.com.cn/Periodical/dqyhjgxxb201601006 YIN Yapeng, LI Xin, ZHENG Xiaobing, et al. Design and implemeng of automated site observing radiometer[J]. Journal of Atmospheric and Environmental Optics, 2016, 11(1):44-50. http://d.old.wanfangdata.com.cn/Periodical/dqyhjgxxb201601006
[3] 顾行发, 田国良, 余涛, 等.航天光学遥感器辐射定标原理与方法[M].北京:科学出版社, 2013:199-200. GU Xingfa, TIAN Guoliang, YU Tao, et al.The radiometric calibration principle and method of space remote sensor[M].Beijing:Science Press, 2013:199-200.
[4] SLATER P N, BIGGAR S F, HOLM R G, et al. Reflectance-and radiance-based methods for the in-flight absolute calibration of multispectral sensors[J]. Remote Sensing of Environment, 2015, 22(1):11-37. doi: 10.1016-0034-4257(87)90026-5/
[5] 胡秀清, 张玉香, 邱康睦, 等.中国遥感卫星辐射校正场科研成果论文选编[M].北京:海洋出版社, 2001. HU Xiuqing, ZHANG Yuxiang, QIU Kangmu, et al. Collected papers of China radiometric calibration site[M]. Beijing:Ocean Press, 2001.
[6] 王润生, 熊盛青, 聂洪峰, 等.遥感地质勘查技术与应用研究[J].地质学报, 2011, 85(11): 1699-1743. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dizhixb201111002 WANG Runsheng, XIONG Shengqing, NIE Hongfeng, et al. Remote sensing geology exploration technology and applied research[J]. Acta Geologica Sinica, 2011, 85(11): 1699-1743. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dizhixb201111002
[7] 林雪松, 王淑荣, 李福田.空间傅里叶变换红外光谱仪用全柔性机构的设计与研究[J].光学精密工程, 2005, 13(6):691-696. doi: 10.3321/j.issn:1004-924X.2005.06.012 LIN Xuesong, WANG Shurong, LI Futian. Design and study of the precision scans structure of space infrared FTS[J].Optics and Precision Engineering, 2005, 13(6):691-696. doi: 10.3321/j.issn:1004-924X.2005.06.012
[8] 李新, 郑小兵, 洪津, 等.高光谱短波红外地物光谱仪光机设计[J].光学精密工程, 2007, 15(11):1656-1661. doi: 10.3321/j.issn:1004-924x.2007.11.004 LI Xin, ZHENG Xiaobing, HONG Jin, et al. Optical and mechanical design of SWIR hyperspectral field spectroradiometer[J]. Optics and Precision Engineering, 2007, 15(11):1656-1661. doi: 10.3321/j.issn:1004-924x.2007.11.004
[9] 左晓舟, 张燕, 杨海成, 等.量化分析技术在光机装调工艺中的应用[J].新技术新工艺, 2015(1):74-77. doi: 10.3969/j.issn.1003-5311.2015.01.026 ZUO Xiaozhou, ZHANG Yan, YANG Haicheng, et al. Application of quantitative analysis in mech-optic assembly and alignment[J]. New Technology & New Process, 2015(1):74-77. doi: 10.3969/j.issn.1003-5311.2015.01.026
[10] 武中华, 袁吕军, 朱永田, 等.特大非球面度离轴非球面补偿器结构设计与装调[J].应用光学, 2017, 38(4): 639-643. http://d.old.wanfangdata.com.cn/Periodical/yygx201704021 WU Zhonghua, YUAN Lyujun, ZHU Yongtian, et al. Structure design and assembling of compensator for off-axis aspheric surface with large asphericity[J]. Journal of Applied Optics, 2017, 38(4): 639-643. http://d.old.wanfangdata.com.cn/Periodical/yygx201704021
[11] 岳鹏远, 赵希婷, 赵振, 等.无焦压缩光路系统的计算机辅助装调方法[J].应用光学, 2016, 37(4): 607-611. http://d.old.wanfangdata.com.cn/Periodical/yygx201604020 YUE Pengyuan, ZHAO Xiting, ZHAO Zhen, et al.Computer-aided alignment method in afocal compressed optical path system[J]. Journal of Applied Optics, 2016, 37(4): 607-611. http://d.old.wanfangdata.com.cn/Periodical/yygx201604020
[12] 黄鲁, 洪津, 汪元均, 等.VF921B型地物光谱仪[J].光电子技术与信息, 1998, 11(5), 37-41. http://d.old.wanfangdata.com.cn/Periodical/gdzjsyxx199805010 HUANG Lu, HONG Jin, WANG Yuanjun, et al. Model VF921B field radiometer[J]. Optoelectronic Technology &Information, 1998, 11(5), 37-41. http://d.old.wanfangdata.com.cn/Periodical/gdzjsyxx199805010
[13] STAYLORW F. Degradation rates of the AVHRR visible channel for the NOAA-6, -7 and -9 spacecraft[J]. Journal of Atmospheric and Oceanic Technology, 1990(7):411-423. https://www.researchgate.net/publication/23575946_Degradation_rates_of_the_AVHRR_visible_channel_for_the_NOAA_6_7_and_9_spacecraft
[14] HOLBEN B N, KAUFMAN Y J, KENDALL J D. NOAA-11 AVHRR visible and near-IR inflight calibration[J]. International Journal of Remote Sensing, 1990, 11(8):1511-1519. doi: 10.1080/01431169008955109
[15] 王广平, 许廷发, 倪国强, 等.多ADSP-TS201红外弱小目标实时检测跟踪系统的硬件设计[J].光学精密工程, 2007, 15(6):941-944. doi: 10.3321/j.issn:1004-924X.2007.06.023 WANG Guangping, XU Tingfa, NI Guoqiang, et al. Hardware design of infrared dim target real time detection and tracking system based on multiple ADSP-TS201S[J]. Optics and Precision Engineering, 2007, 15(6):941-944. doi: 10.3321/j.issn:1004-924X.2007.06.023




 下载:
下载:










 陕公网安备 61011302001501号
陕公网安备 61011302001501号 