Dynamic detection of object deformation based onshearing speckle interferometry
-
摘要: 为使仅适用于静态测量的空间相移剪切散斑干涉系统可用于物体变形的动态测量,在对传统剪切散斑干涉系统加以改进的基础上,提出一种物体变形动态检测方法。将检测系统中的压电陶瓷控制器用参考镜代替,减少了物理装置控制与执行的时间。对于物体发生变形的同一状态,仅需采集一幅干涉图像即可满足后期计算,加以二维连续小波滤波和最小二乘相位解包算法,能满足物体变形动态在线检测的需求。理论和实测实验表明,该方法能快速可靠地检测出物体动态形变,整个系统的最大误差范围在-1.5 rad~1.5 rad之间,整个检测过程最大误差百分比为6.4%,有较高的精度和实用性,为新型剪切散斑干涉测量系统的改进和设计提供参考。Abstract: In order to make the spatial phase-shift shearing speckle-pattern interferometry system for static measurement only be used for dynamic measurement of object deformation, a new dynamic detection method based on improved traditional shear speckle interferometry is proposed.The piezoelectric ceramic transducer (PZT) in testing system is replaced with reference mirror to reduce the control and execute time.For the same state of the distortion of object, only one interferogram needs to be collected to meet later calculation.With two-dimensional continuous wavelet filtering and least-squares phase unpack algorithm, this system can meet the needs of dynamic on-line detection of object deformation.Theoretical and experimental results show that the proposed method can detect the dynamic deformation of the object quickly and reliably, and has high precision and practicability.The maximum error of whole system is in the range of -1.5 rad~1.5 rad and the maximum percentage error of whole detection process is 6.4%.It can provide a reference method for the improvement and design of the new shear speckle interferometry measurement system.
-
Keywords:
- optical measurement /
- deformation detection /
- dynamic detection /
- shearography
-
引言
物体变形的检测是当今研究热点之一,变形检测可分为静态检测和动态检测[1-3]。随着工业现代化、智能化的发展,物体变形的动态检测尤其是工业环境下物体变形的动态在线检测需求显得日益迫切[4-5]。
剪切散斑干涉法(shearography)又称SSPI(shearing speckle pattern interfermetry),采用剪切散斑干涉装置,不需参考光,对环境扰动不敏感,实用性强,是散斑检测方法中工程应用的首选[6-7]。剪切散斑干涉法测的是物体离面位移的一阶微分,在物体变形动态检测上,剪切散斑干涉法更直观,同时也更有效[8-9]。
传统的空间相移SSPI系统中,空间相移是在压电陶瓷(PZT))控制器下执行的,物理装置控制与执行都需要时间[10]。对于同一状态,在不同的时刻和不同的位置采集多幅图像,因此,传统的SSPI测量法难以满足物体变形动态检测的需求,一种新的可用于物体变形动态检测的剪切散斑干涉法是现代工业迫切需求的,有着较大的现实意义。
本文以参考镜代替PZT,系统中无需PZT控制器,对于物体发生变形的同一状态,采集一幅干涉图像即可满足后期计算,再经过二维连续小波滤波和最小二乘相位解包,实现了剪切散斑干涉的物体变形动态测量,实验验证了该方法的有效性和可行性。
1 测量原理
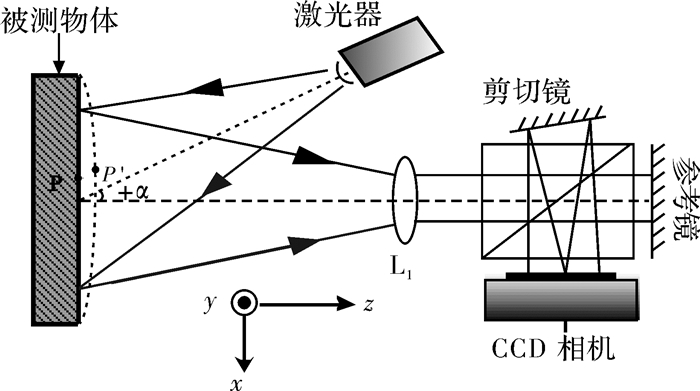
SSPI动态测量系统基本原理如图 1所示,激光器和CCD相机置于xoz面,剪切沿x轴向,剪切量为5 mm。
激光器发出的光照射在漫射体表面,反射光经凸透镜(L1)并在剪切干涉装置中进行光的干涉,成像于CCD阵面。点P[P(x, y, z)]是被测物体未变形时物面上的任意一点,当物体发生变形,则点P移变为点P′[P(x+u, y+v, z+w)],由于照射在点P上的光程不等于照射在点P′上的光程,光程的改变引起了相位的变化,通过物体变形前后相位差的计算,即可得物体的变形情况。图 1中,α是激光束中心线与剪切干涉装置中心线的夹角,且-π/2<α<π/2。
设SSPI测量系统的剪切量沿x轴向,则相位变化[11]可表示为
$$ \Delta \varphi \left( x, y \right)=\frac{2\text{ }\!\!\pi\!\!\text{ }\delta x}{\lambda }[\frac{\partial u}{\partial x}\text{sin}\alpha +\frac{\partial v}{\partial x}\text{sin}\beta +\frac{\partial w}{\partial x}\left( 1+cos\alpha \right)] $$ (1) 式中:u、v、w分别是物体沿x、y、z轴向的位移分量; α、β分别是x-z面和y-z面的光照角。当激光器和CCD相机置于x-z面,且剪切沿x轴向,则相位变化为
$$ \Delta \varphi \left( x, y \right)=\frac{2\text{ }\!\!\pi\!\!\text{ }\delta x}{\lambda }[\frac{\partial w}{\partial x}\left( 1+\text{cos}\alpha \right)+\frac{\partial u}{\partial x}\text{sin}\alpha ] $$ (2) 剪切沿y轴向时的相位变化为
$$ \Delta \varphi \left( x, y \right)=\frac{2\text{ }\!\!\pi\!\!\text{ }\delta y}{\lambda }[\frac{\partial w}{\partial y}\left( 1+\text{cos}\alpha \right)+\frac{\partial u}{\partial y}\text{sin}\alpha ] $$ (3) 当光照角α很小且接近于0时,则离面位移的一阶导数为
$$ \left\{ \begin{align} & \frac{\partial w}{\partial x}=\frac{\lambda }{4\text{ }\!\!\pi\!\!\text{ }\delta x}\Delta \varphi \left( x, y \right) \\ & \frac{\partial w}{\partial y}=\frac{\lambda }{4\text{ }\!\!\pi\!\!\text{ }\delta y}\Delta \varphi \left( x, y \right) \\ \end{align} \right. $$ (4) 即可求出物体的三维变形。
2 滤波原理
小波变换有着时频局部化特性、多分辨率特性、解相关特性和选基灵活性[12-13]。采用电子散斑干涉二维连续小波去噪方法。对于二维图像f(x, y),若以X代表干涉条纹图单个像素的二维坐标,则f(x, y)可写为f(X),其小波变换可表述为
$$ \left\{ \begin{align} & Wf\left( b, a, \theta \right)={{a}^{-n}}\int _{_{-\infty }}^{^{\infty }}f\left( X \right){{\Psi }^{*}}[{{a}^{-1}}{{r}_{-\theta }}\left( X-b \right)]{{d}^{2}}X \\ & \Psi \left( X \right)=\text{exp}(-m{{\left| X \right|}^{2}}+j2\text{ }\!\!\pi\!\!\text{ }X) \\ \end{align} \right. $$ (5) 式中:r-θ是常规的2×2旋转阵; m是窗口调整参数。则二维小波变换(2-D WT)相位计算式:
$$ \varphi \left( b \right)=\text{arctan}[\frac{\text{Im}Wf(b, {{a}_{r, b}}, {{\theta }_{r, b}})}{\text{Re}Wf(b, {{a}_{r, b}}, {{\theta }_{r, b}})-{{f}_{0}}(\text{ }\!\!\pi\!\!\text{ }/m)\text{exp}(-{{\text{ }\!\!\pi\!\!\text{ }}^{2}}/m)}] $$ (6) 式中:ar, b是b点处脊的尺度参数; θr, b是b点处的旋转角,b是小波变换的位置。
为体现二维连续小波去噪效果,经位置布局设计,然后经线性叠加可实现局部条纹的整幅组合。干涉条纹的数学描述以及整幅图的线性组合如下:
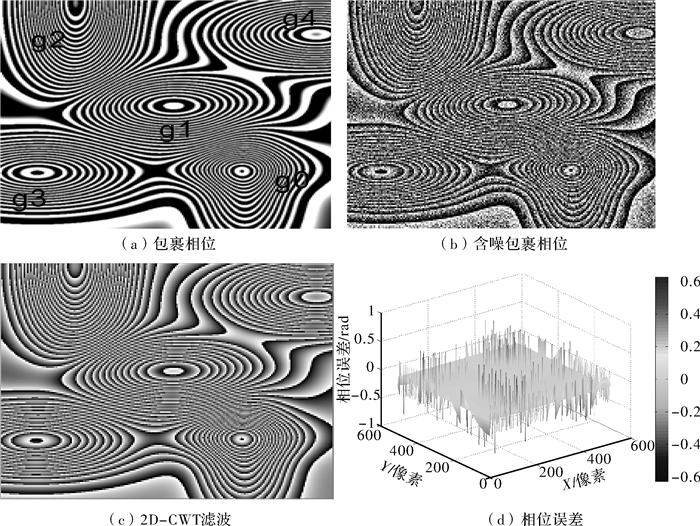
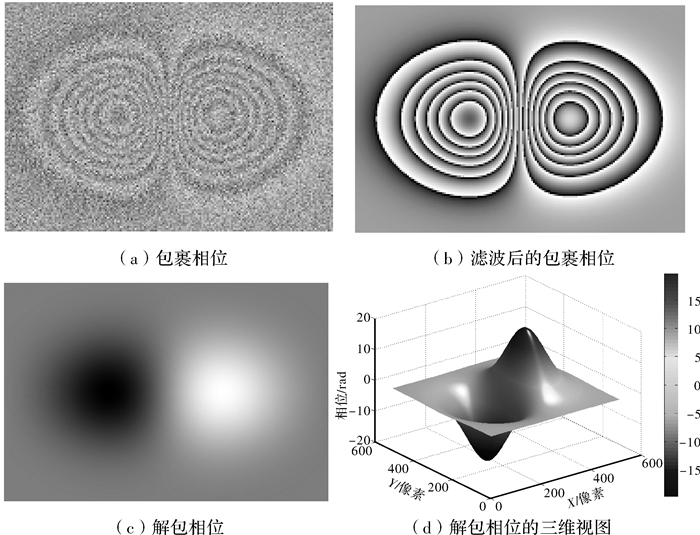
$$ \begin{align} & G0=60\times \text{exp}\left( -\left( {{\left( x-120 \right)}^{2}}/\left( 2\times {{\left( 40 \right)}^{2}} \right)+{{\left( y-160 \right)}^{2}}/\left( 2\times {{\left( 80 \right)}^{2}} \right) \right) \right); \\ & G1=G0-80\times \text{exp}(-({{\left( x\text{ }-10 \right)}^{2}}/(2\times {{\left( 100 \right)}^{2}})+{{\left( \text{ }y\text{ }+20 \right)}^{2}}/(2\times {{\left( 45 \right)}^{2}}))); \\ & G2=G1+120\times \text{exp}(-({{\left( x\text{ }+140 \right)}^{2}}/(2\times {{\left( 50 \right)}^{2}})+{{\left( \text{ }y\text{ }+250 \right)}^{2}}/(2\times {{\left( 120 \right)}^{2}}))); \\ & G3=G2+45\times \text{exp}(-({{\left( x\text{ }-100 \right)}^{2}}/(2\times {{\left( 70 \right)}^{2}})+{{\left( \text{ }y\text{ }-120 \right)}^{2}}/(2\times {{\left( 30 \right)}^{2}}))); \\ & G4=G3+85\times \text{exp}(-({{\left( x\text{ }+200 \right)}^{2}}/(2\times {{\left( 95 \right)}^{2}})+{{\left( \text{ }y\text{ }-130 \right)}^{2}}/(2\times {{\left( 45 \right)}^{2}}))); \\ & G=G4-100\times \text{exp}(-({{\left( x\text{ }-230 \right)}^{2}}/(2\times {{\left( 100 \right)}^{2}})+{{\left( \text{ }y\text{ }+180 \right)}^{2}}/(2\times {{\left( 50 \right)}^{2}}))); \\ \end{align} $$ (7) 二维连续小波去噪原理如图 2。图 2(a)是干涉条纹的包裹相位,其中g0为G0的包裹相位,g1为G1的包裹相位,g2为G2的包裹相位,g3为G3的包裹相位,g4为G4的包裹相位,G的包裹相位即为整幅干涉条纹的包裹相位,如图 2(b)。
对干涉条纹G的包裹相位添加正态分布随机噪声,噪声幅值设为10,含噪相位如图 2(b)。采用二维连续小波去噪方法,对含噪相位图 2(b)去噪,滤波后的相位如图 2(c),从而表明2D-CWT有着良好的去噪效果,且因滤波算法造成的相位误差甚小,如图 2(d),最大误差值为0.732,最小误差值为-0.681,相位误差在-1 rad~ 1 rad之间。
3 实验与讨论
3.1 原理实验
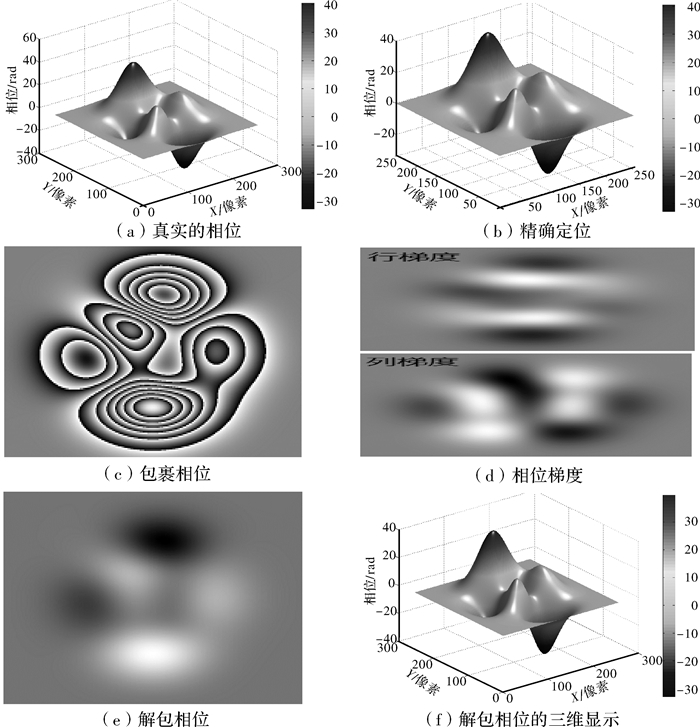
以峰值函数为例,仿真实验如下:图像尺寸设为256×256,峰值函数的幅值设为5,即Pha=5×peaks(256),其相位如图 3所示。图 3(a)为峰值函数的真实相位,为方便于后续比较,进行三维坐标的精确定位显示,如图 3(b)。
峰值函数的包裹相位如图 3(c),取值区间为-π~π,包裹相位沿x、y轴向的梯度即行梯度和列梯度在图 3(d)中分别显示。通过离散余弦变换可得图 3(c)的解包相位,如图 3(e),其三维视图如图 3(f),可以看出解包相位分布于-40 rad~40 rad之间。图 3(b)最大幅值和最小幅值分别为40.52和-32.75,图 3(f)最大幅值和最小幅值分别为39.68和-32.72,比较图 3(b)和图 3(f),解包相位与真实相位基本一致。不仅可视觉上的三维比较,而且可通过解包相位与真实相位的精确比较,解包相位与真实相位的一维、二维曲线,如图 4所示。
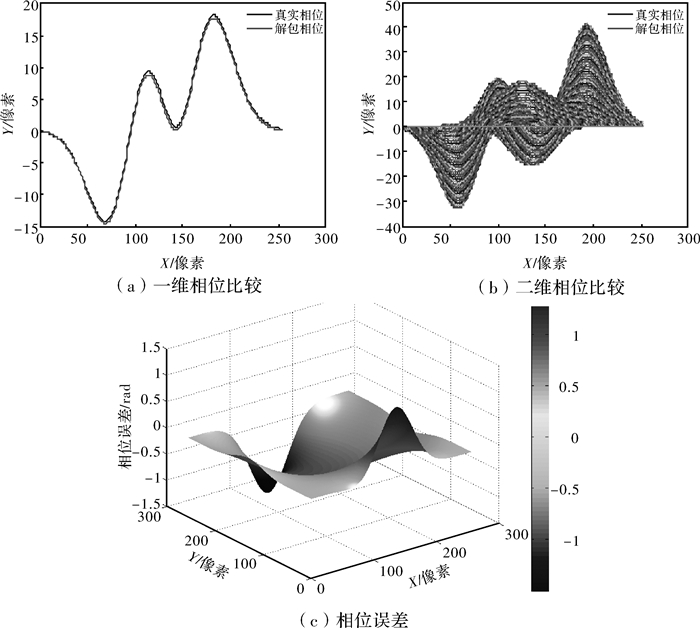
经相位比较,图 4(a)和图 4(b)中解包相位与真实相位的一维、二维曲线都基本一致,误差如图 4(c),误差在-1.5 rad~1.5 rad之间,最大误差1.273,最小误差-1.499,均方误差0.268 6,最大误差百分比为3.9%,如表 1所示。
表 1 仿真实验误差及精度分析单位:rad Table 1. Simulation experimental error andprecision analysis最大幅值 最小幅值 最大误差 最小误差 均方误差 真实相位 40.52 -32.75 1.273 -1.499 0.2686 解包相位 39.68 -32.72 3.2 实测实验
本实验采用边缘加紧中心加载的金属面板进行测量。构件尺寸为120 mm×120 mm,厚度5 mm,使用Baumer TXG08c型工业相机,分辨率776×103 2,最小分辨像素为4.65 μm×4.65 μm,剪切沿x轴向,剪切量为5 mm,实验布置如图 5所示。
He-Ne激光器发出的是红色光,波长为632.8 nm,激光通过反射镜和光束扩展器照射在被测物体上,反射光经成像镜(L1)在剪切干涉装置中发生光的干涉,成像于CCD阵面。CCD相机经图像采集卡与计算机相连,计算机通过图像采集卡读取采集到的图像信息并在计算机上显示。不作加载,物体未发生变形时留存一幅干涉图像,加载操作物体发生变形,通过CCD采集一幅干涉图像,以变形前的图样减去变形后的图样,得变形条纹图样及包裹相位,如图 6所示。
从图 6(a)中可以看出包裹相位中含有大量噪声,采用二维连续小波滤波法进行去噪预处理,滤波后的相位如图 6(b),其相位包裹于-π~π之间,为了得到连续的相位,由LS解包算法进行相位解包裹,解包后的相位分布于-20 rad~20 rad之内,其三维显示如图 6(d),相位最大值为19.66,最小值为-19.024。最大误差为1.156,最小误差为-1.458,均方误差为0.232 6,最大误差百分比为6.1%,如表 2所示。
表 2 实测实验误差及精度分析Table 2. Measured experimental error andprecision analysis最大幅值 最小幅值 最大误差 最小误差 均方误差 真实相位 20.23 -19.103 1.156 -1.458 0.2326 解包相位 19.66 -19.024 对被测物体中心加载施加压力,所加压力由小至大,连续持久施压,若CCD以采样间隔Δt=0.5 s的速度记录不同压力下被测物体发生变形所引起的变形干涉条纹如表 3所示。
表 3 物体的动态变形检测Table 3. Dynamic deformation detection of objectT1 T2 T3 T4 T5 变形干涉条纹 




滤波后的包裹相位 




解包相位三维视图 




CCD采集的图像经计算机在线处理,对T1时刻采集的变形干涉条纹经二维小波滤波,运行时间为23.93 s, 滤波后的包裹相位经最小二乘进行相位解包运行时间为29.63 s, 从干涉条纹采集到变形条纹解包相位的三维显示不到1 min。从T1到T5共计2.5 s,其间采集的5幅变形图样,其检测结果以三维形式显示于表 3中,可以满足工业环境中物体动态变形检测需求。
整个检测过程最大误差为1.425,最小误差为-1.397,最大误差百分比为6.4%,如表 4所示。
表 4 动态变形检测实验误差及精度分析 单位:radTable 4. Dynamic deformation measured experimentalerror and precision analysisT时刻 最大幅值 最小幅值 最大误差 最小误差 T1 11.616 -11.156 0.714 -0.851 T2 17.423 -17.189 0.961 -0.921 T3 29.463 -29.039 1.239 -1.153 T4 41.045 -40.654 1.367 -1.286 T5 46.579 -46.142 1.425 -1.397 4 结论
本文对剪切散斑干涉检测系统原理进行了分析,对检测物体变形的离面位移的一阶导数作了数学推导,对传统空间相移剪切散斑干涉系统加以改进。采用傅里叶变换法,以连续二维小波滤波和最小二乘相位解包法对采集的干涉图像进行处理,实验验证该方法能够有效检测物体的动态变形情况,且其变化情况可在计算机上实时三维显示,能够满足工业环境中物体动态变形检测需求。对于如何进一步缩减计算机的处理时间,对滤波和相位解包算法进行改进将是下一步研究的重点。
-
表 1 仿真实验误差及精度分析
单位:rad Table 1 Simulation experimental error andprecision analysis
最大幅值 最小幅值 最大误差 最小误差 均方误差 真实相位 40.52 -32.75 1.273 -1.499 0.2686 解包相位 39.68 -32.72 表 2 实测实验误差及精度分析
Table 2 Measured experimental error andprecision analysis
最大幅值 最小幅值 最大误差 最小误差 均方误差 真实相位 20.23 -19.103 1.156 -1.458 0.2326 解包相位 19.66 -19.024 表 3 物体的动态变形检测
Table 3 Dynamic deformation detection of object
T1 T2 T3 T4 T5 变形干涉条纹 滤波后的包裹相位 解包相位三维视图 表 4 动态变形检测实验误差及精度分析 单位:rad
Table 4 Dynamic deformation measured experimentalerror and precision analysis
T时刻 最大幅值 最小幅值 最大误差 最小误差 T1 11.616 -11.156 0.714 -0.851 T2 17.423 -17.189 0.961 -0.921 T3 29.463 -29.039 1.239 -1.153 T4 41.045 -40.654 1.367 -1.286 T5 46.579 -46.142 1.425 -1.397 -
[1] Fu Yu, Pedrini G, Hennelly B M, et al. Dual-wavelength image-plane digital holography for dynamic measurement[J]. Optics and Lasers in Engineering, 2009, 47(5): 552-557. doi: 10.1016/j.optlaseng.2008.10.002
[2] Bhaduri B, Jtay C, Quan C, et al. Two wavelength simultaneous DSPI and DSP for 3D displace-ment field measurements[J]. Optics Communications, 2011, 284(10): 2437-2440. http://cn.bing.com/academic/profile?id=669ee019fd24b4369cc185155c8d8fa2&encoded=0&v=paper_preview&mkt=zh-cn
[3] Lin Zhenheng. A method to extract carrier-wave speckle pattern fringe skeletons based on modulat-ion direction[J]. Acta Photonica Sinica, 2012, 41(7): 800-804. doi: 10.3788/gzxb20124107.800
[4] 冯家亚, 王永红, 王鑫, 等.基于4f的大视角剪切散斑干涉系统设计[J].应用光学, 2015, 36(2):188-193. http://www.yygx.net/CN/abstract/abstract10575.shtml Feng Jiaya, Wang Yonghong, Wang Xin, et al. Design of digital shearography with wide angle of view based on 4f system[J]. Journal of Applied Optics, 2015, 36(2):188-193. http://www.yygx.net/CN/abstract/abstract10575.shtml
[5] 王颖, 吴峰, 付国平, 等.基于散乱三维点云的缺陷检测和三维重构方法[J].应用光学, 2016, 37(3):402-406. http://www.yygx.net/CN/abstract/abstract10791.shtml Wang Ying, Wu Feng, Fu Guoping, et al. Method for defects detection and 3D reconstruction based on dispersed points cloud[J]. Journal of Applied Optics, 2016, 37(3):402-406. http://www.yygx.net/CN/abstract/abstract10791.shtml
[6] Hung Y Y. Speckle-shearing interferometric camera: a tool for measurement of derivatives of surface-displacement[J]. Technical Symposium, 1974, 41:169-176. doi: 10.1117/12.953850
[7] Hung Y Y, Wang J Q. Dual-beam phase shift shearography for measurement of in-plane strains[J]. Optics and Lasers in Engineering, 1996, 24(5-6):403-413. doi: 10.1016/0143-8166(95)00098-4
[8] 高越, 符师桦, 蔡玉龙, 等.数字剪切散斑干涉法研究铝合金中Portevin-Le Chatelier带的离面变形行为[J].物理学报, 2014, 63(6):194-199. http://d.old.wanfangdata.com.cn/Periodical/wlxb201406028 Gao Yue, Fu Shihua, Cai Yulong, et al. Digital shearography investigation on the out-plane deformation of the Portevin-Le Chatelier bands[J]. Acta Phys. Sin., 2014, 63(6):194-199. http://d.old.wanfangdata.com.cn/Periodical/wlxb201406028
[9] 郭媛, 陈小天.基于最小二乘相位解包裹改进算法的研究[J].中国激光, 2014, 41(5):189-194. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201405034 Guo Yuan, Chen Xiaotian. Study of an improved phase unwrapping algorithm based on least squares[J]. Chinese Journal Lasers, 2014, 41(5): 189-194. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201405034
[10] Hung Y Y, Chen Y S, Ng S P, et al. Review and comparison of shearography and active thermography for nondestructive evaluation[J]. Materials Science and Engineering, 2009, 64(5-6):73-112. doi: 10.1016/j.mser.2008.11.001
[11] 郭媛, 毛琦, 陈小天, 等.双波长剪切散斑干涉法在复合材料缺陷检测中的应用[J].光子学报, 2015, 44(3):0312001-1-5. http://d.old.wanfangdata.com.cn/Periodical/gzxb201503028 Guo Yuan, Mao Qi, Chen Xiaotian, et al. Applied research of dual-wavelength sharography for flaw detection of composite materia[J]. Acta Photonica Sinica, 2015, 44(3):0312001-1-5. http://d.old.wanfangdata.com.cn/Periodical/gzxb201503028
[12] 郭媛, 毛琦, 陈小天, 等.干涉条纹快速加窗傅里叶滤波方法的研究[J].光学学报, 2014, 34(6): 0612008-1-5. http://www.cnki.com.cn/Article/CJFDTotal-GXXB201406025.htm Guo Yuan, Mao Qi, Chen Xiaotian, et al. Study of a fast windowed Fourier filtering method for interference fringes[J]. 2014, 34(6): 0612008-1-5. http://www.cnki.com.cn/Article/CJFDTotal-GXXB201406025.htm
[13] Bahich M, Bailich M, Imloul A, et al. A comparative study of one and two-dimensional wavelet-based techniques for noisy fringe patterns analysis[J]. Optics Communications, 2013, 290: 43-48. doi: 10.1016/j.optcom.2012.10.054
-
期刊类型引用(1)
1. 孙广开,李红,吴越,张旭,何彦霖,祝连庆. 遥感航天器在轨结构微变形光纤监测技术发展综述. 仪器仪表学报. 2022(12): 1-14 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载:


 陕公网安备 61011302001501号
陕公网安备 61011302001501号 