Hole target detection and location of complex workpiece based on binocular vision
-
摘要:
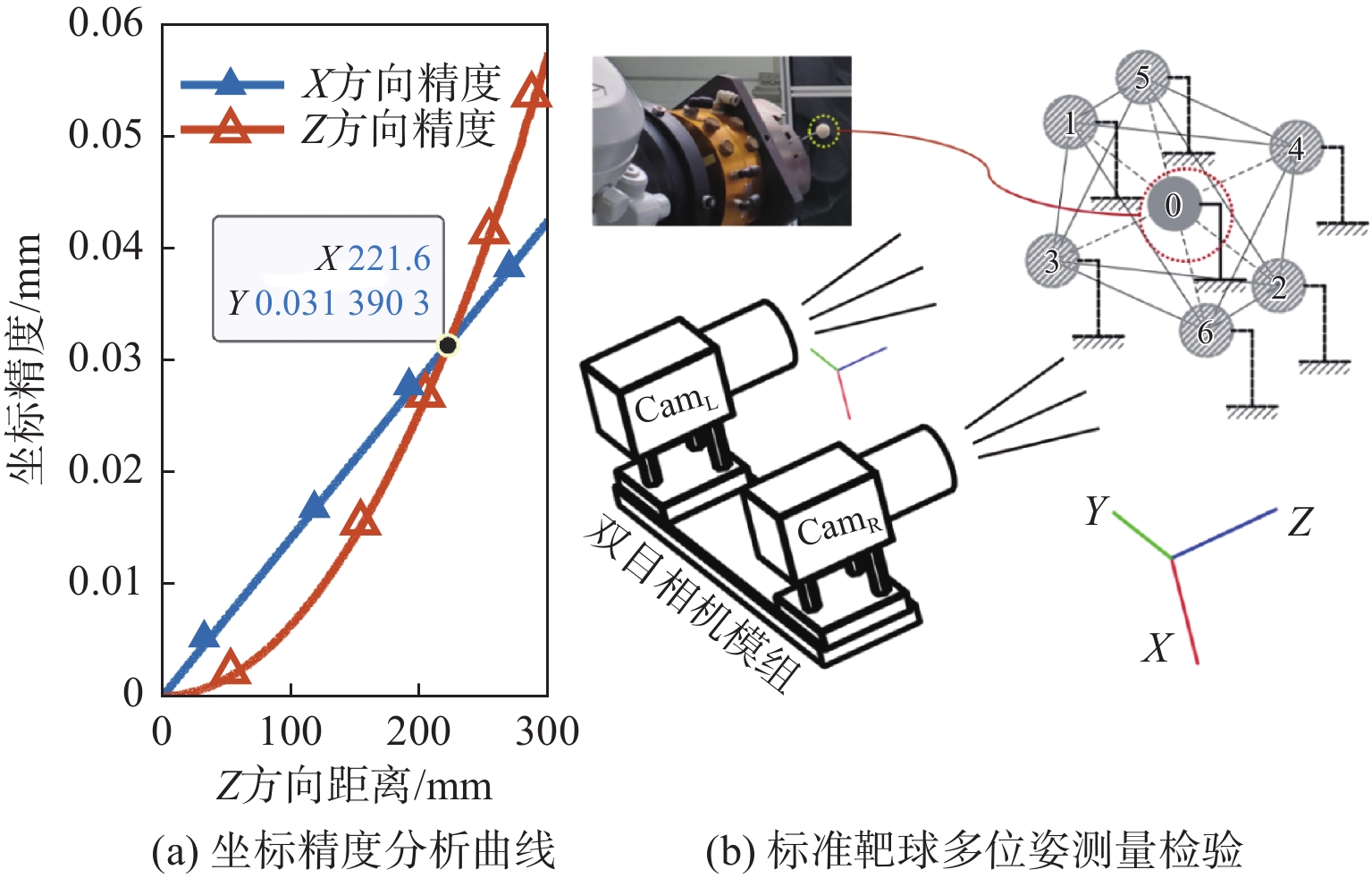
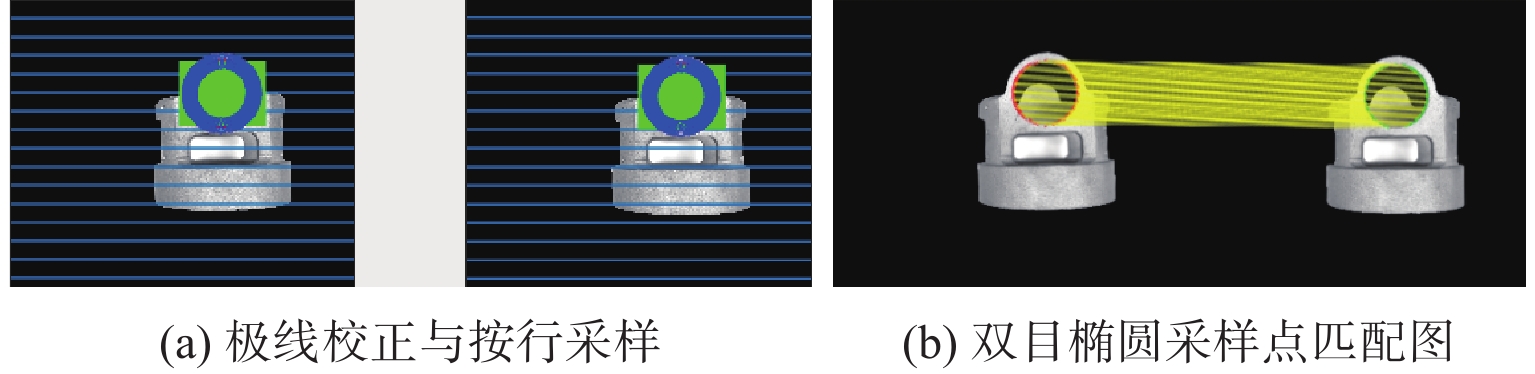
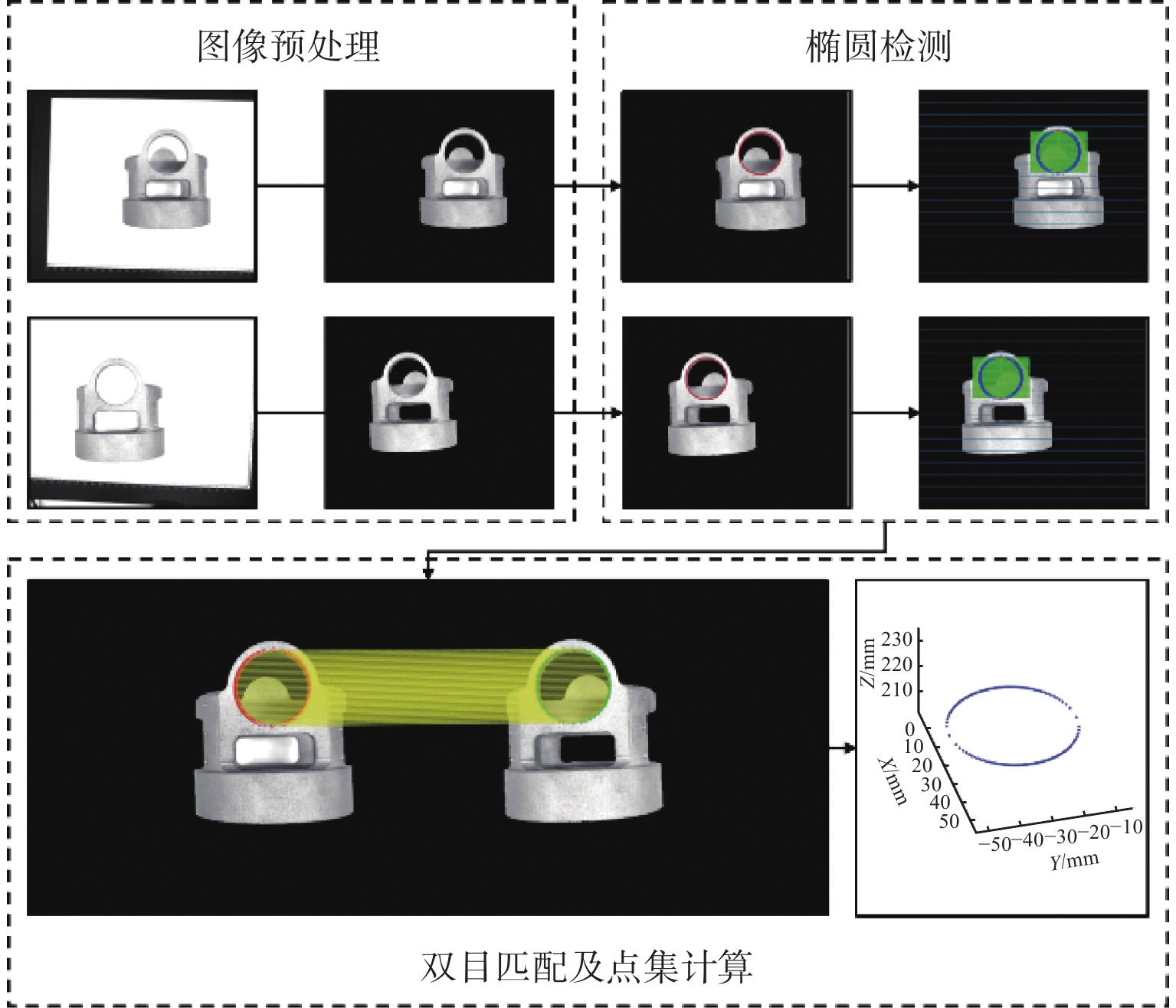
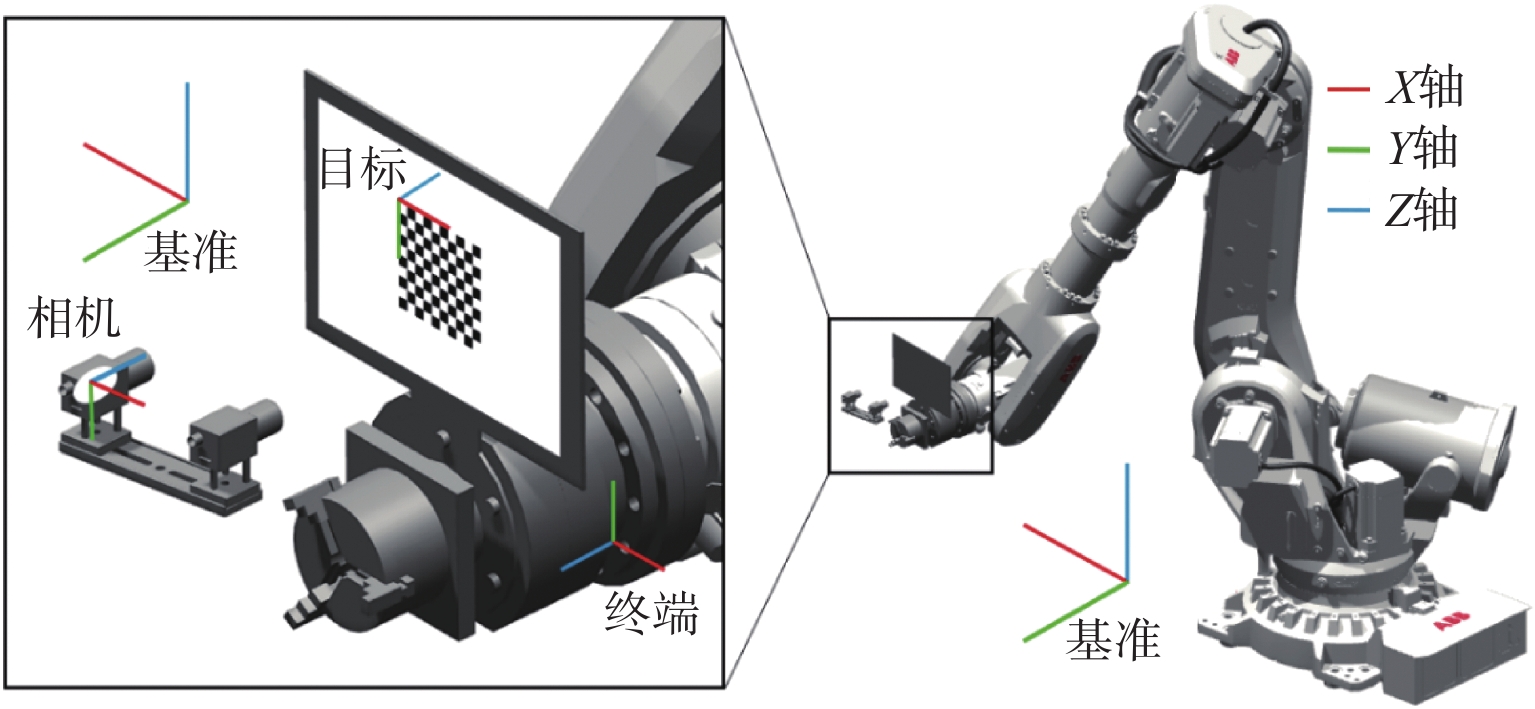
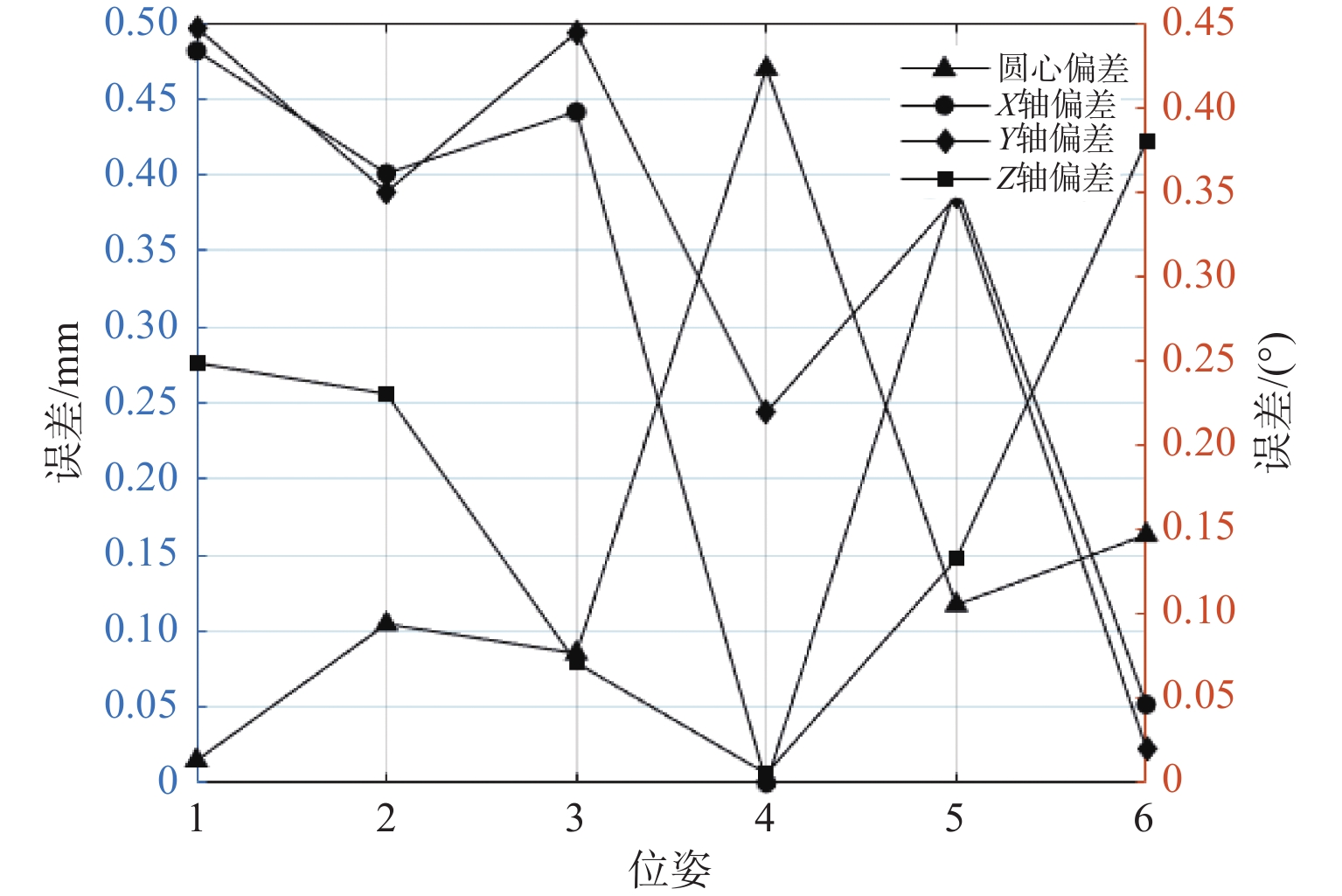
针对金属3D打印件孔洞部位支撑残留后处理问题,提出了一种双目视觉检测定位方法。测量系统基于弧段椭圆识别算法进行工件孔位检测,通过计算待加工孔位在双目模组主相机光心坐标系中的位姿、并将该位姿转换到加工现场机械臂基坐标系,为离线编程和自动加工提供坐标信息。首先标定双目相机并检验硬件系统对标定角点的测量精度;然后对复杂工件的待加工位置椭圆特征进行提取,基于极线校正后图像对左右图椭圆进行同行像素点采集和双目匹配;最终根据多视图原理进行匹配点对的坐标计算,进而输出带有坐标信息的空间圆环。对双目相机模组进行了标定靶球测量验证实验,结果显示尺寸测量误差小于0.20 mm。对实际工件进行了测量定位实验,结果表明,该系统测量圆孔尺寸的最大误差小于0.84%,圆心空间位置误差小于0.50 mm,圆环姿态最大误差小于0.5°。
Abstract:A binocular vision detection and positioning method was proposed to solve the problem of post-processing of hole support residue in metal 3D printing parts. The hole position of the workpiece was detected by the measuring system based on the arc ellipse recognition algorithm. By calculating the pose of the hole position to be machined in the optical center coordinate system of the main camera in binocular module, and converting the pose to the base coordinate system of the robot arm on machining site, the coordinate information was provided for off-line programming and automatic machining. Firstly, the binocular camera was calibrated and the measurement accuracy of the hardware system was checked. Then, the position ellipse features of the complex workpiece to be processed were extracted, and the parallel pixel acquisition and binocular matching were carried out for left and right image ellipses based on the pole-corrected images. Finally, the coordinates of matching point pairs were calculated according to the multi-view principle, and the spatial ring with coordinate information was output. A calibration target ball measurement verification experiment was carried out for binocular camera module. The results show that the measurement error is less than 0.20 mm. The measurement and positioning experiment of the actual workpiece was carried out. The results show that the maximum error of the system is less than 0.84%, the error of the center space is less than 0.50 mm, and the maximum error of the attitude of the ring is less than 0.5°.
-
引言
在雾霾、浑浊水体等环境中,由于悬浮的微粒、水滴对传输光的散射作用,图像的能见度和成像对比度显著降低,使得成像质量下降,对观察目标和进一步的图像处理产生了诸多影响。同时,随着科技的发展,无人机、自动驾驶和水下机器人等应用对图像的依赖越来越强,对图像质量的要求也越来越高,因此,去雾、去散射成像技术受到了广泛关注[1-3]。根据处理方式的不同,去雾、去散射成像技术可主要分为图像处理去散射技术和光学去散射技术[4-5]。
图像处理技术又可以分为两类:一种是基于图像增强的算法,图像增强技术通常不考虑成像环境的影响,利用图像处理的方法直接增强图像对比度,代表方法如直方图均衡化算法[6]、Retinex[7]算法等。该技术的优点在于计算速度快,对应用环境没有限制,适用场景广泛;但处理过程中会丢失一定信息或图像过度增强,稳定性不高,同时噪声抑制能力弱。另一种是基于物理模型的图像复原算法,主要通过特定的模型或先验假设来估算图像的退化参量,利用该参量进行图像复原。该技术的优点在于复原图像保真度高、细节还原能力强;缺点是算法复杂度高、耗时久,适用范围有限,代表方法如暗通道先验算法[8]、SCHECHNER Y Y的偏振差分法[9]、TAN R T的单图像去雾法[10]等。近年来基于深度学习的去散射方法也在快速发展。相较于传统算法,神经网络提升了参数估计的准确性,去雾效果更加显著。典型方法是CAI B等人[11]利用卷积神经网络(CNN)学习大气散射模型中的透射率t(x)来对图像进行去雾。AOD-Net[12]、DCPDN[13]都是极具代表性的算法,该类方法虽然提升了参数估计的准确性,但仍然依赖于大气散射模型,存在参数估计偏差的弊端。
区别于其他图像处理技术,光学去散射技术往往基于特定的光学系统,通过获取对应不同光学参数(光谱、偏振等)的多张图像实现散射光抑制或剔除[14]。由于散射光(天空中的大气散射光或水下环境中的背向散射光)具有明显的部分偏振特性,因此在诸多光学去散射技术中,偏振去散射技术性能突出。基于偏振成像的复原方法可以从多幅不同的偏振图像中获得更多的信息,理论上可以获取到细节增强的去散射图[15]。代表方法有SCHECHNER Y Y等人将偏振理论应用到去散射(去雾)领域,假设大气光是部分偏振光,物体光是非偏振光,利用两幅偏振图像进行差分处理,基于传统的大气退化模型构建了偏振差分去散射模型。周文舟[16]等人提出一种基于多尺度奇异值分解的图像融合去散射算法,利用偏振测量信息的冗余特性,采用最小二乘法提高了传统偏振图像去散射算法中偏振信息的准确度,定性分析了偏振图像融合去散射的可行性。2021年,LIANG J[17]等人基于3张偏振子图,提出了一种针对偏振度和偏振角做低通滤波的偏振去散射方法。对于浑浊水下,LI X B[6]等人通过将传统的偏振差分模型和数字图像增强算法相结合,实现了高浑浊水体环境下的图像复原,且效果明显。到目前为止,已有大量偏振方法可以有效地恢复特定场景下的退化图像,但是这些方法的复原效果很依赖于能否准确估计场景中的各种偏振参数。在强散射场景中,偏振光场分布是非常复杂的,估算出所需的偏振参数十分具有挑战性,这是限制偏振去散射算法的一大难题[18-19]。2022年,DONG Z M[20]等人提出了一种利用灰度方差选择合适的偏振图像的恢复算法,尝试在低偏振光场景下做去散射处理,取得了一定的效果。但是灰度方差是一个侧重图像全局灰阶分布的指标,而图像的偏振信息分布往往具有区域分布特点,在一幅图像中通常只有部分区域具有比较高的偏振度,比如场景中天空、建筑物的窗户、金属材料等存在高偏振物质区域,存在关键参数估算精度不高的缺点。
针对散射介质中图像对比度提升问题,本文提出一种基于主动照明调制的水下散射抑制成像方法,在获取目标场景以及背景位置穆勒矩阵的基础上,结合计算方法对主动照明斯托克斯矢量进行调制,从而确定最佳偏振照明调制,进而实现后向散射光偏振度的最大化,最终对后向散射光最大程度抑制。实验结果表明,本方法在高浑浊度散射介质中成像效果明显,可实现对后向散射的抑制,图像对比度提升明显,图像复原结果接近空气中或微弱散射情况下人眼的视觉效果。此外,该方法采用“点对点”散射抑制,不会出现数字图像处理依赖于图像块灰度分布以及滤波器的使用所造成的图像细节丢失、图像模糊、图像噪点增加等问题,可应用于散射介质成像、散射介质目标检测与识别等场景。
1 方法
水下散射介质成像过程中,成像装置所接收到的光强主要包括两部分:第一部分为受到散射环境中散射粒子散射以及吸收作用的目标物体反射光 $ {I_{\mathrm{T}}} $;第二部分为主动照明所导致的后向散射光 $ {I_{\mathrm{B}}} $。相机接收的光强$ I $ 主要为以上两部分的非相干叠加:
$$ I = {I_{\mathrm{T}}} + {I_{\mathrm{B}}} $$ (1) 一般认为图像中背景位置没有目标光,只存在后向散射光。在具有主动照明的水下散射环境中,后向散射光一般为部分偏振光,其偏振状态以及偏振度将会受到主动照明光源的偏振状态、偏振度以及散射介质等因素的影响。对于水下成像中后向散射光的获取,一般认为如果图像中存在背景(无穷远处的无目标)区域,那么成像系统在此处接收到的光即被认为只存在后向散射。因此,可以通过提取图像中无穷远处的背景来对散射介质的后向散射进行计算。
假设光源到背景之间散射介质的穆勒矩阵为$ {{\boldsymbol{M}}^{{\mathrm{back}}}} $,入射主动照明光场斯托克斯矢量为$ {\boldsymbol{S}}^{\mathrm{in}} $,背景处后向散射光的斯托克斯矢量为${\boldsymbol{S}}^{\mathrm{back}}$,则三者之间的关系如下所示:
$$ {{\boldsymbol{S}}^{{\mathrm{back}}}} = {\left[ {\begin{array}{*{20}{c}} {s_0^{{\rm{back}}}}&{s_1^{{\rm{back}}}}&{s_2^{{\rm{back}}}}&{s_3^{{\rm{back}}}} \end{array}} \right]^{\rm{T}}} = {{\boldsymbol{M}}^{{\rm{back}}}} \cdot {{\boldsymbol{S}}^{{\rm{in}}}} $$ (2) 为达到最佳抑制效果,在介质穆勒矩阵$ {{\boldsymbol{M}}^{{\mathrm{back}}}} $固定的情况下,需要通过调制偏振生成仪(PSG)改变入射光${{\boldsymbol{S}}^{{\mathrm{in}}}}$,从而改变后向散射光$ {{\boldsymbol{S}}^{{\mathrm{back}}}} $,进而对后向散射光偏振度进行调控,最终实现在后向散射光偏振度达到最大值时,通过调制成像系统中的偏振分析仪(PSA)对后向散射光中的偏振部分进行抑制。
入射光${{\boldsymbol{S}}^{{\mathrm{in}}}}$可表示为
$$ {{\boldsymbol{S}}^{in}} = \left[ {\begin{array}{*{20}{c}} {s_0^{{\rm{in}}}} \\ {s_1^{{\rm{in}}}} \\ {s_2^{{\rm{in}}}} \\ {s_3^{{\rm{in}}}} \end{array}} \right] = s_0^{in}\left[ {\begin{array}{*{20}{c}} 1 \\ {P\cos 2\alpha \cos 2\varepsilon } \\ {P\sin 2\alpha \cos 2\varepsilon } \\ {P\sin 2\varepsilon } \end{array}} \right] $$ (3) 式中:$P$为入射光偏振度;$\alpha $为偏振椭圆长轴方位角;$\varepsilon $为偏振椭圆椭偏率;$s_0^{{\mathrm{in}}}$为入射主动照明光照强度。为尽量提高后向散射光偏振度,同时符合偏振产生装置PSG实际调制情况,入射光为完全偏振光,因此$P$被设置为1。
实际上,后向散射光偏振度${P_{{\mathrm{back}}}}$越高,相当于越大比例的后向散射光可以被偏振分析装置PSA所抑制。在每一种入射主动照明偏振光条件下都会产生一个相应的后向散射光偏振度${P_{{\mathrm{back}}}}$,即后向散射光最大的偏振度由入射主动照明决定。因此,通过确定最大的后向散射光偏振度即可确定最优主动照明,最优入射主动照明光椭圆方位角${\alpha _{{\mathrm{opt}}}}$以及椭偏率${\varepsilon _{{\mathrm{opt}}}}$可根据式(4)确定。
$$ \left( {{\alpha _{{\rm{opt}}}},{\varepsilon _{{\rm{opt}}}}} \right) = {\mathop {\arg }\limits_{\left( {\alpha ,\varepsilon } \right)} }\; {\max \left\{ {{P_{{\rm{back}}}}\left( {{{\boldsymbol{M}}^{{\rm{back}}}},\alpha ,\varepsilon } \right)} \right\}} $$ (4) 根据偏振度定义,后向散射光偏振度${P_{{\mathrm{back}}}}$可表示为式(5):
$$ \begin{gathered} {P_{{\rm{back}}}}\left( {{{\boldsymbol{M}}^{{\rm{back}}}},\alpha ,\varepsilon } \right) = \frac{1}{{s_0^{{\rm{back}}}}}{\left[ {{{\left( {s_1^{{\rm{back}}}} \right)}^2} + {{\left( {s_2^{{\rm{back}}}} \right)}^2} + {{\left( {s_3^{{\rm{back}}}} \right)}^2}} \right]^{\tfrac{1}{2}}} \;\;\;\;\;\;\;\;\\ = \frac{1}{{\displaystyle\sum\limits_{j = 0}^3 {{\boldsymbol{M}}_{0j}^{{\rm{back}}}s_j^{{\rm{in}}}\left( {\alpha ,\varepsilon } \right)} }}{\left\{ {\displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 0}^3 {{{\left[ {{\boldsymbol{M}}_{ij}^{{\rm{back}}}s_j^{{\rm{in}}}\left( {\alpha ,\varepsilon } \right)} \right]}^2}} } } \right\}^{\tfrac{1}{2}}} \\ \end{gathered} $$ (5) 根据式(5)可以看出,当场景确定后,介质的穆勒矩阵$ {{\boldsymbol{M}}^{{\rm{back}}}} $固定不变,因此,后向散射光偏振度为方位角$\alpha $以及椭偏率$\varepsilon $的函数,可通过式(6)所示求导并验根的方法,对此二元函数最大值解析解${\alpha _{{\mathrm{opt}}}}$与${\varepsilon _{{\mathrm{opt}}}}$进行求取。
$$ \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\partial {P_{{\rm{back}}}}\left( {{{\boldsymbol{M}}^{{\rm{back}}}},\alpha ,\varepsilon } \right)}}{{\partial \alpha }} = 0} \\ {\dfrac{{\partial {P_{{\rm{back}}}}\left( {{{\boldsymbol{M}}^{{\rm{back}}}},\alpha ,\varepsilon } \right)}}{{\partial \varepsilon }} = 0} \end{array}} \right. $$ (6) 当入射光确定后,后向散射光也随之确定,此时可根据后向散射光偏振度${P_{{\rm{back}}}}$对后向散射光进行分解,分别得到后向散射光中偏振光以及非偏振光部分,并将其分别表示为$ \boldsymbol{S}_{\mathrm{p}}^{\rm{back}} $以及$ \boldsymbol{S}_{\mathrm{u}}^{\rm{back}} $,表达式如式(7)所示:
$$ \left. {\begin{array}{*{20}{l}} {{\boldsymbol{S}}_{\mathrm{p}}^{{\rm{back}}} = {{\left[ {\begin{array}{*{20}{c}} {{P_{{\rm{back}}}}s_0^{{\rm{back}}}}&{s_1^{{\rm{back}}}}&{s_2^{{\rm{back}}}}&{s_3^{{\rm{back}}}} \end{array}} \right]}^{\rm{T}}}} \\ {{\boldsymbol{S}}_{\mathrm{u}}^{{\rm{back}}} = {{\left[ {\begin{array}{*{20}{c}} {\left( {1 - {P_{{\rm{back}}}}} \right)s_0^{{\rm{back}}}}&0&0&0 \end{array}} \right]}^{\rm{T}}}} \end{array}} \right\} $$ (7) 由于$ \boldsymbol{S}_{\mathrm{p}}^{\rm{back}} $为完全偏振光,因此只需令成像系统中偏振分析装置PSA的偏振特征矢量${\boldsymbol{A}}$为式(8)所示,即可满足二者互相正交,从而实现对后向散射光中的偏振部分$ \boldsymbol{S}_{\mathrm{p}}^{\rm{back}} $进行最大程度的抑制。
$$ \begin{gathered} {\boldsymbol{A}} = \frac{1}{{{P_{{\rm{back}}}}s_0^{{\rm{back}}}}}{\left[ {\begin{array}{*{20}{c}} {{P_{{\rm{back}}}}s_0^{{\rm{back}}}}&{ - s_1^{{\rm{back}}}}&{ - s_2^{{\rm{back}}}}&{ - s_3^{{\rm{back}}}} \end{array}} \right]^{\rm{T}}}\;\;\;\;\;\;\;\; \\ = {\left[ {\begin{array}{*{20}{c}} 1&{ - \dfrac{{s_1^{{\rm{back}}}}}{{{P_{{\rm{back}}}}s_0^{{\rm{back}}}}}}&{ - \dfrac{{s_2^{{\rm{back}}}}}{{{P_{{\rm{back}}}}s_0^{{\rm{back}}}}}}&{ - \dfrac{{s_3^{{\rm{back}}}}}{{{P_{{\rm{back}}}}s_0^{{\rm{back}}}}}} \end{array}} \right]^{\rm{T}}} \\ \end{gathered} $$ (8) 在实际光学系统中,可通过调制PSA中的偏振光学元器件(即线偏振片和四分之一波片)的状态来实现具体偏振特征矢量A。不失一般性假设PSA中线性偏振片P-2的透振方向与水平方向夹角为$\gamma $,四分之一波片WP-2快轴与水平方向夹角为$ \theta $,那么此时偏振分析装置PSA的特征向量如式(9)[21]所示:
$$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1 \\ {{{\cos }^2}\left( {2\theta } \right)\cos \left( {2\gamma } \right) + \sin \left( {2\theta } \right)\cos \left( {2\theta } \right)\sin \left( {2\gamma } \right)} \\ {\sin \left( {2\theta } \right)\cos \left( {2\theta } \right)\cos \left( {2\gamma } \right) + {{\sin }^2}\left( {2\theta } \right)\sin \left( {2\gamma } \right)} \\ { - \sin \left( {2\theta } \right)\cos \left( {2\gamma } \right) + \cos \left( {2\theta } \right)\sin \left( {2\gamma } \right)} \end{array}} \right] $$ (9) 计算可得此时成像装置接收到的图像$ I(x,y) $如式(10)所示:
$$ \begin{split} &I(x,y) = \frac{1}{2}{{\boldsymbol{A}}^{\mathrm{T}}}{\boldsymbol{S}}\left( {x,y} \right) = \\ &\frac{1}{4}\left\{ {2{s_0}\left( {x,y} \right) + {s_1}\left( {x,y} \right)\left[ {\cos \left( {4\theta - 2\gamma } \right){\text{ + }}\cos \left( {2\gamma } \right)} \right] + } \right. \\ &{s_2}\left( {x,y} \right)\left[ {\sin \left( {4\theta - 2\gamma } \right) + \sin \left( {2\gamma } \right)} \right] - \left.{2{s_3}\left( {x,y} \right)\sin \left( {2\theta - 2\gamma } \right)} \right\} \end{split} $$ (10) 式中:$\left( {x,y} \right)$为图像像素坐标位置;${\boldsymbol{S}} = {\left[ {{s_0}}\;\;{{s_1}}\;\;{{s_2}}\;\;{{s_3}} \right]^{\mathrm{T}}}$为场景出射光透过PSA之前的斯托克斯矢量。${\boldsymbol{S}} $可通过入射光斯托克斯矢量$ \boldsymbol{S}\mathrm{^{in}} $与整个场景穆勒矩阵$ {\boldsymbol{M}} $得到,计算公式如式(11)所示:
$$ {\boldsymbol{S}} = {\boldsymbol{M}} \cdot {{\boldsymbol{S}}^{{\rm{in}}}} = \left[ {\begin{array}{*{20}{c}} {{m_{00}}}&{{m_{01}}}&{{m_{02}}}&{{m_{03}}} \\ {{m_{10}}}&{{m_{11}}}&{{m_{12}}}&{{m_{13}}} \\ {{m_{20}}}&{{m_{21}}}&{{m_{22}}}&{{m_{23}}} \\ {{m_{30}}}&{{m_{31}}}&{{m_{32}}}&{{m_{33}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {s_0^{{\rm{in}}}} \\ {s_1^{{\rm{in}}}} \\ {s_2^{{\rm{in}}}} \\ {s_3^{{\rm{in}}}} \end{array}} \right] \;\;\;\;$$ (11) 2 实验与结果分析
2.1 实验平台搭建
基于上述理论,设计可行性验证实验,搭建用于穆勒矩阵成像的偏振光学探测系统。实验装置如图1所示,其中P-1和P-2为2个线偏振片,WP-1和WP-2为2个四分之一波片,实验中可通过对照明光源入射方向以及出射方向的四分之一波片及线性偏振片进行分时机械旋转,并同步采集不同条件下的图像,经过最终计算来得到场景穆勒矩阵。图1中位于入射方向的P-1和WP-1组合构成偏振生成仪(polarization state generate, PSG),负责生成主动偏振光照明;P-2以及WP-2组合构成偏振分析仪(polarization state analysis, PSA),用于实现待测偏振光的偏振解算和偏振分析。
实验中所使用光源为中心波长625 nm的LED光源(THORLABS, M625L3);成像装置为德国 Allied Vision Technologies 公司 Stingray 系列14位数字CCD灰度相机F-033B,其像素为 492×656;高透玻璃水缸作为容器,尺寸大小为15 cm×15 cm×40 cm;偏振片为THORLABS的LPVISE200-A线性偏振片,其消光比大于$ 1\ 000:1 $;四分之一波片为THORLABS的WPQ20ME-633,其延迟准确度小于${\lambda \mathord{\left/ {\vphantom {\lambda {100}}} \right. } {100}}$,延迟均匀性小于5 nm;电控旋转台的重复定位精度为${0.1^ \circ }$,平行度$100\;{\text{μm}}$,速度${25^ \circ }$/s,分辨率为${0.01^ \circ }$;目标物被置于距离水缸前侧15 cm处,目标为白色塑料板上的塑料贴纸(贴纸内容为:数字 4,“耳朵”图标以及尺子)以及黑色记号笔所写“TJU”字迹。
实验时,首先需模拟浑浊水下成像环境,利用牛奶作为实验场景常用的散射介质,因其具有分散均匀的特点,能够出色地仿制海水的散射特性,将其和去离子水加入水缸中,搅拌均匀,用来模拟浑浊水下散射环境。选用波长625 nm的光源是因为在可见光范围内,随着波长增加,散射系数逐渐减小,表现出近似反比例的趋势,在相同的探测距离下,红光相对于其他波长的可见光,经历的散射事件较少,这有助于维持后向散射光的较高偏振度水平。为了便于探测器更好地接收目标反射信息,系统中主动照明光源入射光束方向与相机接收到的反射光束夹角大致呈${21^ \circ }$。
2.2 图像采集与处理
在散射介质成像实验中,为对所测得穆勒矩阵进行恰当显示同时便于计算,此处将测量得到的场景穆勒矩阵16幅图相对于左上角图片进行归一化处理,相当于将图像场景中每一个坐标点穆勒矩阵的16个数值相对于左上角${m_{00}}$进行归一化,最终实验场景归一化穆勒矩阵测量结果如图2所示。
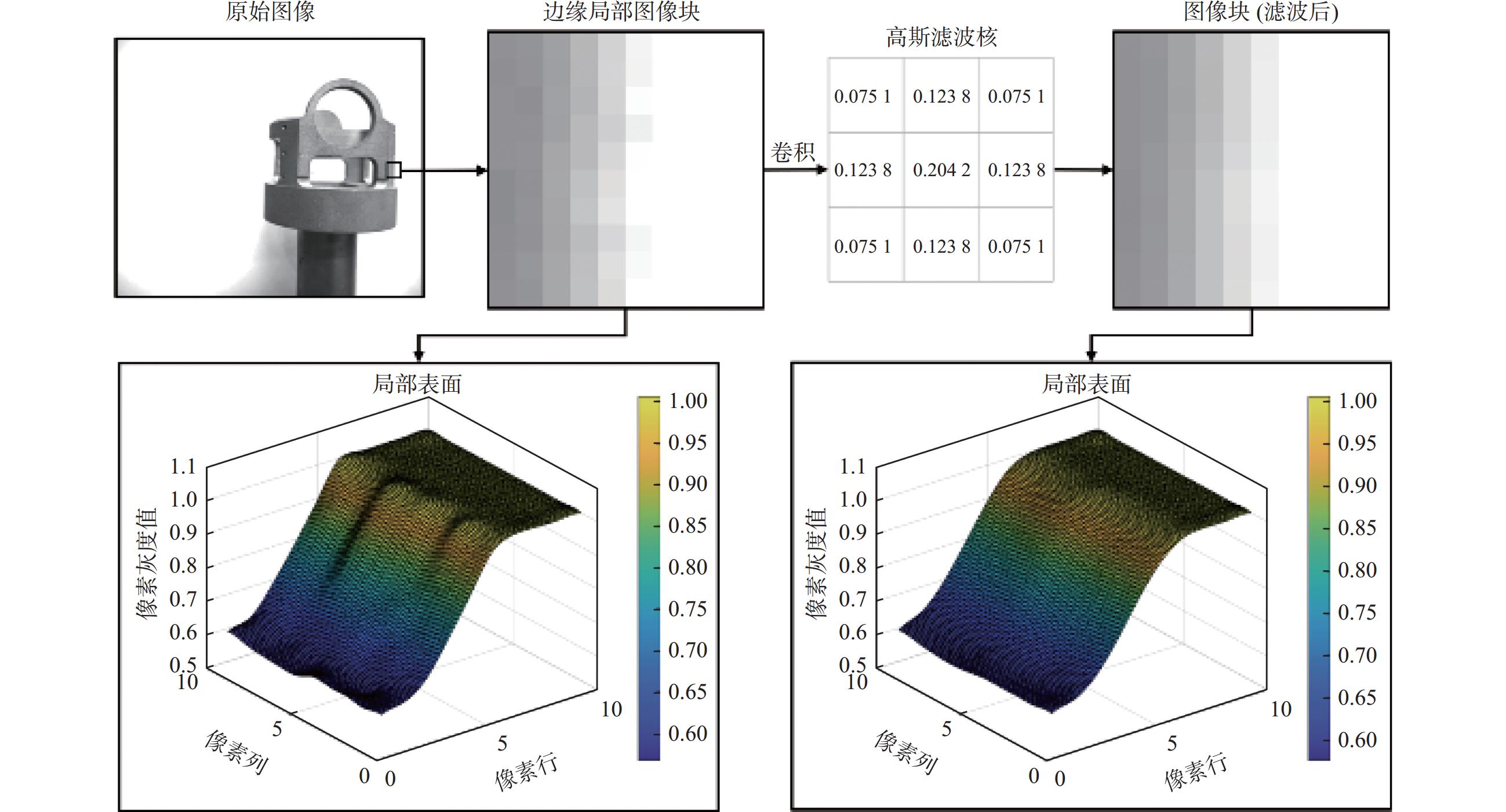
基于测得的斯托克斯矢量进行图像反演解算,从而得到上述理论中背景位置的穆勒矩阵和目标物的穆勒矩阵,这两个矩阵分别用来描述背景处散射环境对于入射光场的调制能力和目标场景对于入射光场的调制能力,这种调制不光体现在光强这一信息,也体现在更高维度如对偏振的调制。值得注意的是,本文展示的方法具体实施时背景区域通过人工选定,但实际操作中也可通过四叉树分层搜索[22]等方法实现自动背景区域选定,全部计算成像流程见图3。
利用式(4)~式(6),迭代解出最优入射主动照明光椭圆方位角${\alpha _{{\mathrm{opt}}}}$以及椭偏率${\varepsilon _{{\rm{opt}}}}$,由此确定最优的入射光偏振态${{\boldsymbol{S}}^{{\rm{in}}}}$,同时可以解出PSA的最优特征向量。经过这一系列偏振解算,通过电控旋转台对PSG进行调节约束相应的入射光束${{\boldsymbol{S}}^{{\rm{in}}}}$,对PSA调节约束其偏振特征矢量${\boldsymbol{A}}$,之后进一步经过成像系统的采集,得到偏振解算处理后的图像。我们的方法通过PSA对输出的图像进行直接调制,CCD相机采集得到的便是散射抑制后的成像结果。
2.3 图像复原和算法对比分析
将本文提出的浑浊介质偏振去散射成像方法与其他几种典型方法进行对比,结果如图4所示,其灰度直方图分布结果如图5所示。其中强度图像(Intensity image)为未经计算成像处理前,入射光经过散射介质由普通光强相机所拍摄光强图像,其结果与人眼观察视觉效果较为相近,HSI为光强图像经直方图拉伸处理后结果。可以看出,在主动照明情况下,由散射介质引起的后向散射光较为强烈,照明光场经散射后,使得目标物体看起来像是被蒙上了一层“白雾”,图像对比度提升有限,场景中目标依旧难以分辨。且HSI仅对光强图中灰度值进行拉伸而不做任何其他处理,当光强图像中由于成像设备感光芯片存在坏点或图像噪声过大导致图像中存在极值时,其拉伸效果就会受到明显影响,这将直接导致即使对图像进行了拉伸处理,但其灰度分布仍然无法占满整个灰度空间,从而使得拉伸效果大打折扣。对比度限制自适应直方图均衡(CLAHE)[23]与多尺度Retinex均为数字图像处理方法,其依赖于图像块的灰度分布以及滤波器的使用,这种算法在图像增强过程中会导致部分图像细节的丢失,其更适合于提升散射介质中整体图像观感。暗通道先验(DCP)[24]是一种统计意义上的方法,HE K等人对大量户外无雾的图像进行总结,发现在无雾图像中局部区域存在一些像素位置,这些位置对应的R、G、B通道图像中至少存在一个通道的灰度值非常低,且这些低灰度值对应区域不包括天空。DCP可以对灰度图像进行处理,但由于灰度图像通道单一且DCP对于高浑浊度强散射介质中整体偏白的光强图像处理存在缺陷,因此此处效果一般。反之,本方法对应的结果细节保留更好,处理后图像更接近于无散射介质中人眼视觉呈现效果,后续可继续结合数字图像处理的方法,对偏振散射抑制后的结果进行进一步图像增强以及图像去噪等处理,从而得到更高质量的图像复原效果。
此外,观察处理后图像的灰度分布结果可以发现,HSI的灰度范围拉伸是最有限的,并没有布满整个灰度空间,体现在图像中的视觉效果便是对比度效果很差,CLAHE和Retinex的灰度峰值与主要灰度值的分布范围较为接近,两种方法的整体视觉效果相差不大,但由于其峰值所处位置不同,明显CLAHE的图像会更亮一些。观察DCP方法处理后的直方图,其峰值分布虽未紧密连接但却分布在一定的区间内,由于其在复原目标反射光的图像处理过程中对散射抑制不完全,以至于将主动照明的非均匀性进行凸显,使得图像视觉效果变差。
为了进一步验证所提方法的有效性,我们测试了分辨率板的成像复原效果,原始图像及不同复原结果的对比如图6所示。值得注意的是,为了验证本文所提方法的先进性,我们增添了基于低秩稀疏分解(LRSD)的去散射方法[25]进行对比。其中Ours-1表示由上述模型直接得到的呈现结果,Ours-2是在Ours-1的基础上采用CLAHE处理后进一步提升后的结果。
从图6可直观看出,所有方法相比于原始光强图已有很大的提升,但DCP处理后图像背景处的强度高于其他方法的背景强度,这是由于暗通道先验方法基于统计规律,对光场强度估计不准确导致了强度分布不均匀,Ours-1方法便消除了这种背景光场分布不均匀的情况。对比采用的4种方法中,Ours-2的对比度提升最为明显,其细节轮廓部分更为清晰,背景与目标物的分界处轮廓、数字轮廓、分辨率条纹轮廓、右侧密集条纹轮廓均与周围场景鲜明分割,但同时注意到图像表面有许多暗点,这是由于在大幅增强图像细节的同时,噪声信号也被放大,但其处理结果所包含的信息量仍然是最多的。
对照图7,可以更清楚地看到,原始光强图的整个强度值是偏高的,灰度分布过于集中,经LRSD处理后,其灰度值曲线出现显著变化,在字符处的灰度值下降明显。Retinex与DCP相比,在开始的像素灰度值变化过程中,差异并不明显,其峰值和最小值基本一致,但在对应图像中右侧由背景板向细密小条纹过度的区域,DCP方法明显具有更好的成像效果与成像对比度。DCP方法与Ours-1方法相比,整体变化趋势都是Ours-1的灰度变化更为显著,相应成像细节也更为清晰。而Ours-2方法的灰度值分布曲线不光在边界变化处具有显著的对比度差异,即使在右侧的细密小条纹处,也可以将细节变换清晰地展现出来,将不同目标鲜明地分割出来,极大地改善了成像效果。
为了量化评估,采用图像增强测量(EME)[26]、标准差(STD)[27]、信息熵(Entropy)[28]和对比度(C)[29]4个评价指标对图6中的原始光强图及处理结果进行评判,见表1。EME指标更注重图像的局部细节表现,相比于光强图,LRSD方法的EME提升了70.7%,Retinex提升了201.5%,DCP方法提升了204.5%,Ours-1提升了360.7%,是DCP提升的1.8倍,Ours-2提升了
1047.7 %,是DCP的5.2倍、Ours-1的2.9倍,Ours-2对于细节的改善是巨大的。STD指标与对比度指标均用来描述像素灰度值的离散程度,值越高代表着像素值的差异性越大,像素之间的亮暗对比也就越明显,Ours-2方法处理后的图像,STD和对比度的值皆提升了2倍以上,与Ours-1方法相比也有60%的提升,这表明Ours-2方法在图像整体对比度上的提升也十分显著。图像的信息熵Entropy通常用来描述图像的信息量,熵越高,信息量越高,但要注意的是,引入噪声也会使得图像信息熵增加,故对于信息熵的评价并非是越高越好,要综合考虑成像效果,且对于图像评价要综合考虑多个指标,不可单一使用信息熵来作为评判,就此幅光强图像的处理结果而言,其图像信息量是最大的。表 1 图6中光强图及不同算法客观评价指标Table 1. Objective evaluation indicators for light intensity images and different algorithms in Fig. 6指标 光强图 LRSD DCP Retinex Ours-1 Ours-2 EME 1.128 1.925 3.435 3.401 5.197 12.946 STD 0.017 0.040 0.048 0.033 0.041 0.067 Entropy 6.912 7.361 7.513 7.302 7.383 7.745 C 0.220 0.526 0.404 0.467 0.354 0.518 3 结论
本文提出了一种基于主动偏振照明调制实现水下散射光抑制的偏振成像方法,可以通过偏振照明优化调制实现后向散射光的偏振度最大化,从而最大程度地提升后向散射光的抑制效果。该方法在获取目标场景穆勒矩阵的基础上,通过结合计算方法对主动照明进行偏振优化调制,从而实现后向散射光偏振度最大化,最终实现将后向散射部分最大程度的抑制。本方法首先测量得到目标场景穆勒矩阵以及背景位置穆勒矩阵;其次直接给定后向散射光为完全偏振光时的斯托克斯矢量,并根据给定斯托克斯矢量以及背景位置穆勒矩阵确定入射主动照明斯托克斯矢量;接着求得与后向散射光斯托克斯矢量相互正交的偏振特征矢量;最终通过结合入射主动照明斯托克斯矢量、目标场景穆勒矩阵、目标场景背景位置穆勒矩阵、所求偏振特征矢量对散射介质中图像进行复原。实验结果和不同方法的对比结果表明,本方法可以有效提升浑浊水体下的成像退化问题,并显著提升图像质量。
-
表 1 双目相机系统标定参数
Table 1 Calibration parameters of binocular camera system
参数 左相机 右相机 焦距 $ (2\text{ }413.39,\; 2\text{ }408.07) $ $ (2\text{ 447}\text{.07},\;2\text{ }448.61) $ 径向畸变 $( - 0.125{\text{ }}7,0.214{\text{ }}6,0.009{\text{ }}1)$ $( - 0.098{\text{ }}2{\text{ }},0.144{\text{ 8}}, - 0.043{\text{ 3}})$ 切向畸变 $(0.003{\text{ 2}},0.000{\text{ 7}})$ $( - 0.001{\text{ 5}},0.000{\text{ 9}})$ 旋转矩阵 $\left[ {\begin{array}{*{20}{r}} {0.999\;7}&{0.021\;5}&{ - 0.013\;7} \\ { - 0.021\;3}&{0.999\;7}&{0.015\;6} \\ {0.014\;1}&{ - 0.015\;3}&{0.999\;8} \end{array}} \right]$ 平移向量 $ \left[-51.535\text{ 9},-0.027\text{ 3},-0.758\text{ 3}\right] $ 表 2 标准球测量结果
Table 2 Measurement results of criterion sphere
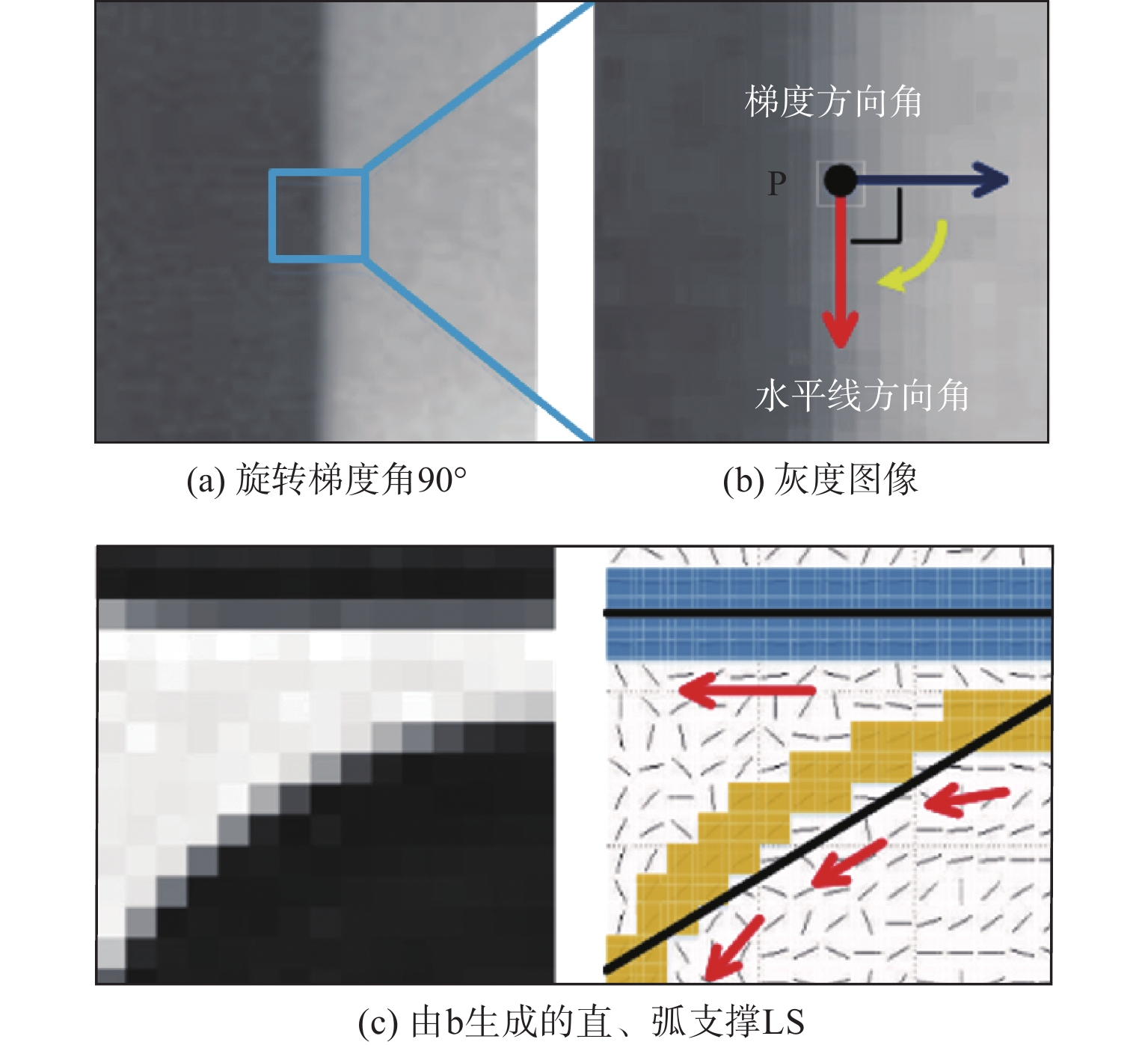
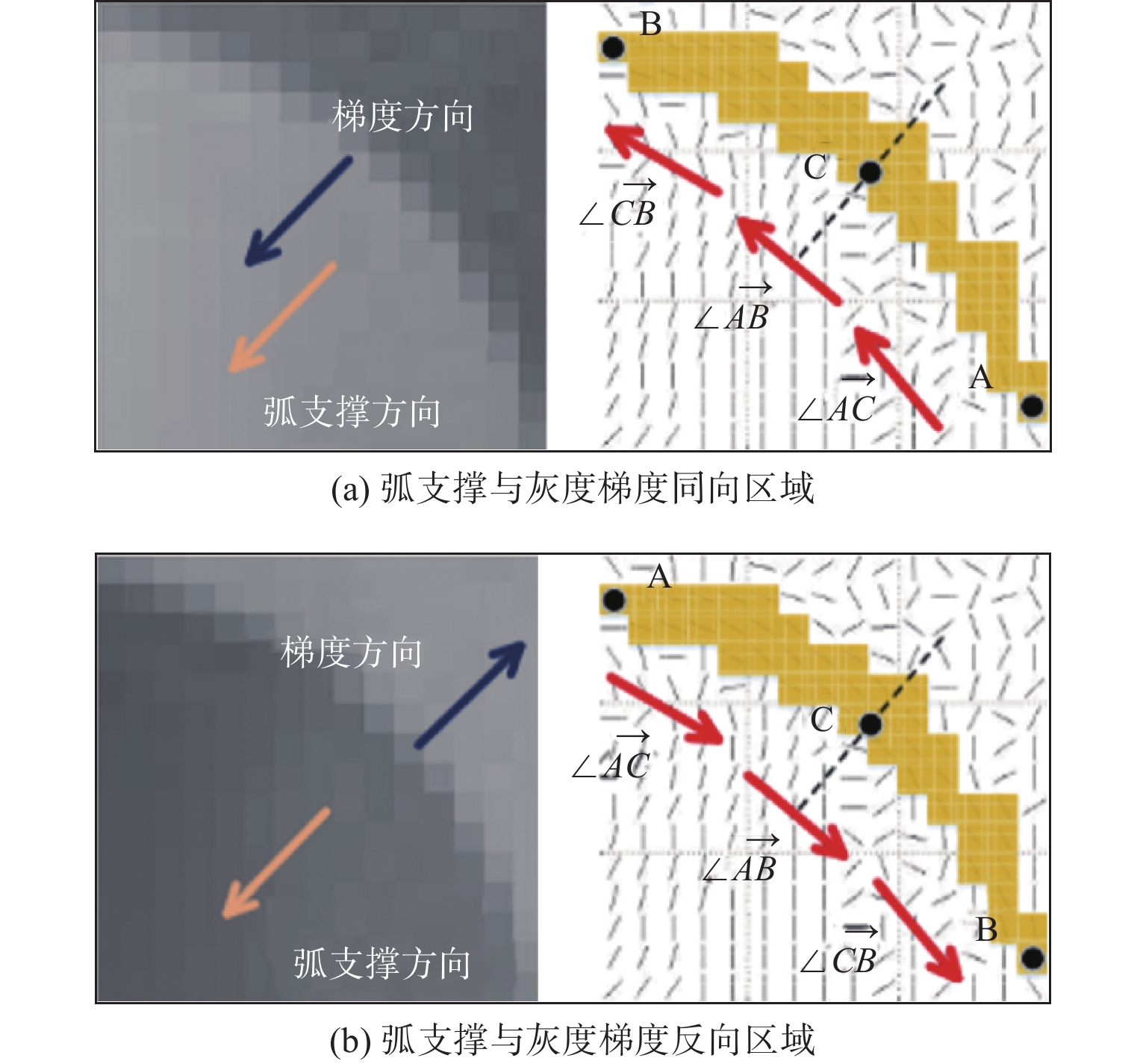
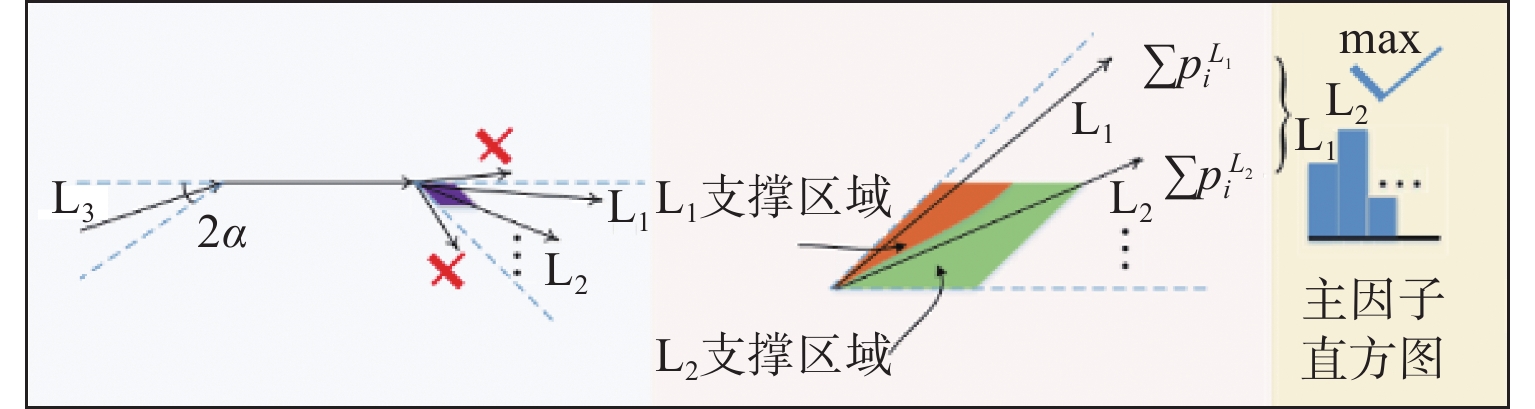
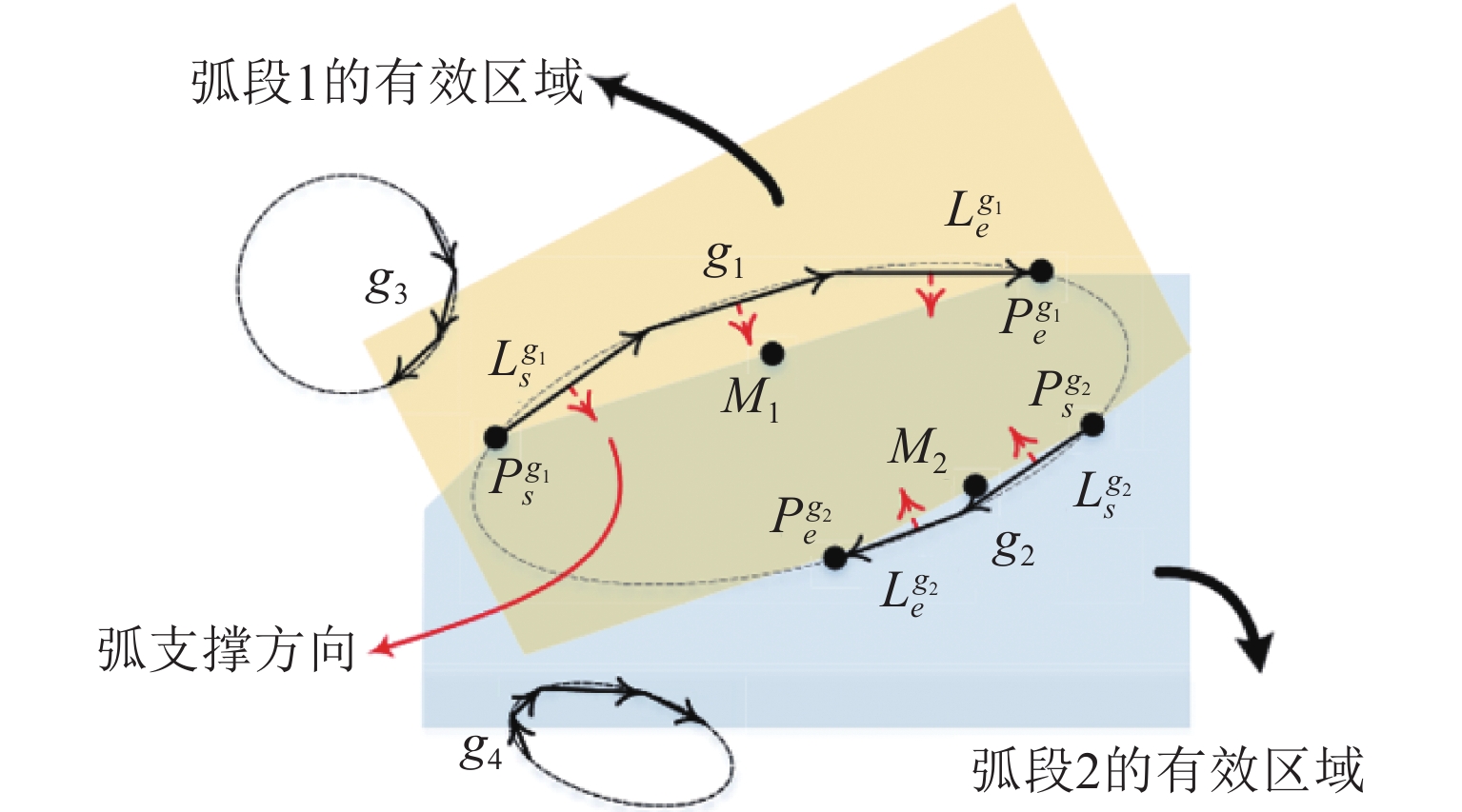
位置序号/参数项 测量结果/mm 偏差(绝对值)/mm 0 20.008 0.020 1 20.151 0.162 2 19.869 0.119 3 20.171 0.183 4 20.116 0.128 5 19.943 0.045 6 20.013 0.025 真值 19.988 mm 最大误差 0.183 mm 均方根误差 0.106 mm 算法1 弧支持组形成过程伪代码 输入:弧支撑线段集${T_l}$;生成线段的圆弧支撑区域${T_r}$;包容角度$\alpha $;线段使用状态参数$S$ 1: 初始化:$G = \emptyset $; 2: 循环: 3: || 从${T_l}$中选择${l_i}$,选择条件:$S({l_i}) \ne used$;设定:${g_{head}} = \emptyset $,${g_{tail}} = \emptyset $,${l_i} \Rightarrow $线段${l_s}$的晶核; 4: || 循环: 5: || | 在${l_s}$的头端搜索连续的弧支撑线段; 6: || | 从搜索结果中排除:$S = used$,到${l_s}$的角度偏差超过$2\alpha $; 7: || | 计算${l_s}$头端的统计面积,使用${T_r}$获得票数最高的线段${l_k}$; 8: || | 刷新:${g_{head}} = {g_{head}} \cup {L_k}$,$S({l_k}) = used$,${l_s} = {l_k}$; 9: || 直到:${l_s} = \emptyset $; 10: || 设定:${l_i} \Rightarrow $线段${l_s}$的生长核;在${l_s}$的尾部重复上述搜索过程即可得到${g_{tail}}$; 11: || ${g_{head}} = \{ {L_{h1}}, \cdots ,{L_{hn}}\} $,${g_{tail}} = \{ {L_{t1}}, \cdots ,{L_{tn}}\} $$ \Rightarrow g = \{ {L_{tn}}, \cdots ,{L_{t1}},{L_i},{L_{h1}}, \cdots ,{L_{hn}}\} $ 12: || 刷新:$G = G \cup g$,$S({l_i}) = used$; 13: 直到:遍历所有弧支撑线段; 14: 返回:$G$; 输出:弧支撑群$G$ 表 3 工件位姿初值
Table 3 Initial values of workpiece pose
圆心坐标/mm 法向量夹角/($^\circ $) X轴 Y轴 Z轴 $[22.60, - 33.25,216.62]$ $88.13$ $88.50$ $2.40$ -
[1] 杨鑫, 王婉琳, 范亚卓, 等. 3D打印金属零件后处理研究现状[J]. 功能材料, 2020, 51(5): 5043-5052 YANG Xin, WANG Wanlin, FAN Yazhuo, et al. Research status of post-processing of 3D printing metal parts[J]. Journal of Functional Materials, 2020, 51(5): 5043-5052.
[2] 朱福康, 刘毅, 孟凡杰, 等. 基于图像深度信息集的Hough圆检测方法[J]. 组合机床与自动化加工技术, 2018(5): 85-88. ZHU Fukang, LIU Yi, MENG Fanjie, et al. Hough circles detection based on depth information set of image[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2018(5): 85-88.
[3] 罗哉, 赵洪楠, 江文松, 等. 基于线激光扫描的基准孔检测与定位方法[J]. 仪器仪表学报, 2021, 42(12): 184-190. LUO Zai, ZHAO Hongnan, JIANG Wensong, et al. A detection and positioning method for the base hole based on line laser scanning[J]. Chinese Journal of Scientific Instrument, 2021, 42(12): 184-190.
[4] 姜春英, 闫子龙, 牛祥鑫, 等. 基于局部主动轮廓模型的飞机壁板铆接孔定位方法研究[J]. 航空制造技术, 2019, 62(10): 58-63. JIANG Chunying, YAN Zilong, NIU Xiangxin, et al. Research on positioning method of aircraft panel riveting hole based on local active contour model[J]. Aeronautical Manufacturing Technology, 2019, 62(10): 58-63.
[5] 张太恒, 梅标, 乔磊, 等. 纹理边界引导的复合材料圆孔检测方法[J]. 浙江大学学报 (工学版), 2020, 54(12): 2294-2300. ZHANG Taiheng, MEI Biao, QIAO Lei, et al. Detection method for composite hole guided by texture boundary[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(12): 2294-2300.
[6] HO C C, ZHANG R H. Machine vision-based relative-angle measurement system between circular holes[J]. Measurement and Control, 2021, 54(5/6): 647-657.
[7] LI D H, NAN F, XUE T, et al. Circle detection of short arc based on randomized Hough transform[C]//2017 IEEE International Conference on Mechatronics and Automation (ICMA). Takamatsu: IEEE, 2017: 258-263.
[8] CHEN S L, XIA R B, ZHAO J B, et al. A hybrid method for ellipse detection in industrial images[J]. Pattern Recognition, 2017, 68: 82-98. doi: 10.1016/j.patcog.2017.03.007
[9] CAKIR H I, BENLIGIRAY B, TOPAL C. Combining feature-based and model-based approaches for robust ellipse detection[C]//2016 24th European Signal Processing Conference (EUSIPCO). Budapest: IEEE, 2016: 2430-2434.
[10] HASAN S F, SADAT R M N, RAHMAN M A, et al. A precise and low complexity distance and size measurement of circular objects from camera position using still images[C]//2006 International Conference on Electrical and Computer Engineering. Dhaka: IEEE, 2006: 439-442.
[11] LU C S, XIA S Y, SHAO M, et al. Arc-support line segments revisited: an efficient high-quality ellipse detection[J]. IEEE Transactions on Image Processing, 2020, 29: 768-781. doi: 10.1109/TIP.2019.2934352
[12] MEI X, SUN X, ZHOU M C, et al. On building an accurate stereo matching system on graphics hardware[C]//2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops). Barcelona: IEEE, 2011: 467-474.
[13] ROTHER C, KOLMOGOROV V, BLAKE A. GrabCut: interactive foreground extraction using iterated graph cuts[M]//Seminal graphics papers: pushing the boundaries: Volume 2. New York: ACM, 2023: 593-598.
[14] 理查德·哈特利, 安德鲁·西塞曼. 计算机视觉中的多视图几何[M]. 韦穗, 杨尚骏, 章权兵, 等, 译. 2版. 合肥: 机械工业出版社, 2019: 211-214. RICHARD H, ANDREW Z. Multiple view geometry in computer vision[M]. WEI S, YANG S J, ZHANG Q B, et al, Transl. 2nd ed. Hefei: Machinery Industry Press, 2019: 211-214.
[15] 李英硕, 杨帆, 袁兆奎. 空间圆形拟合检测新方法[J]. 测绘科学, 2013, 38(6): 147-148. LI Yingshuo, YANG Fan, YUAN Zhaokui. A detection method for 3D circle fitting[J]. Science of Surveying and Mapping, 2013, 38(6): 147-148.




 下载:
下载:












 陕公网安备 61011302001501号
陕公网安备 61011302001501号 