Effect of non-Gaussian term on dynamic light scattering measurement at ultra-low concentrations
-
摘要:
采用去除和保留非高斯项方法，分别反演了不同分布宽度颗粒的模拟动态光散射数据，并通过相应的光强自相关函数(autocorrelation function, ACF)与平均粒径对应的光强ACF间的差值，计算出不同分布宽度颗粒的粒度信息在光强ACF中的分布。结果表明，对于窄分布颗粒，在较低噪声水平下，去除与保留非高斯项对颗粒粒度分布反演无明显影响。随着噪声水平的增高，去除非高斯项反演的性能指标优于保留非高斯项。对于宽分布颗粒（变异系数一般大于3%），保留非高斯项则可得到更为准确的反演结果。产生上述结果的原因在于，不同分布宽度颗粒对应的非高斯项中的粒度信息含量不同。与窄粒度分布相比，宽分布颗粒对应的非高斯项包含更多的粒度信息，去除非高斯项会导致粒度信息丢失，从而降低反演结果的准确性。由于光强ACF的长延迟时段含有较多噪声，窄分布颗粒的反演不仅不能通过保留非高斯项获益，而且还会因噪声增加使反演结果的准确性降低。
Abstract:The simulated dynamic light scattering data of particles with different distribution widths were inverted using the methods of removing and retaining the non-Gaussian term. The distribution of the particle size information in the light intensity autocorrelation function (ACF) with different distribution widths was calculated by the differences between the light intensity ACF and the light intensity ACF corresponding to the average particle size. The results show that for narrow distribution particle systems, the removal and retention of non-Gaussian term have no obvious effect on the inverted particle size distribution at lower noise levels. As the noise level increases, the performance indices of inversion results by removing non-Gaussian term are better than that of by retaining non-Gaussian term. For wide distribution particle systems (coefficients of variation typically greater than 3%), retaining the non-Gaussian term can yield more accurate inversion results. The reason for the above results is that the content of particle size information in the non-Gaussian term corresponding to particles with different distribution widths is different. Compared with narrow distribution particle systems, the non-Gaussian term corresponding to wide distribution particle systems contains more particle size information. The removal of non-Gaussian term can lead to the loss of some particle size information, thereby reducing the accuracy of the inversion results. Since the long-delay period of the intensity ACF contains more noise, the inversion of narrow distribution particles not only cannot benefit from retaining non-Gaussian term, but also reduces the accuracy of inversion results due to the increase of noise.
-
引言
动态光散射（dynamic light scattering, DLS）技术是一种测量亚微米及纳米颗粒粒度分布的有效方法[1-2]，已广泛应用于材料、化工、食品、生物、医药等领域[3-7]。该技术通过测量布朗运动颗粒的散射光信号，实时计算出散射光强自相关函数（autocorrelation function, ACF），再由Siegert关系得到电场ACF，通过反演电场ACF得到颗粒粒度分布（particle size distribution, PSD）[8]。然而，DLS测量受限于样品浓度，当颗粒浓度过低时，所测的散射光强度波动不仅来自颗粒的布朗运动，也来自散射体积中的颗粒数量波动，这一数量波动会在光强ACF的长延迟时段产生一个非高斯项[9]。非高斯项的存在使得光强ACF与电场ACF不再满足Siegert关系，采用经典方法进行DLS反演时，该非高斯项会被作为大颗粒布朗运动产生的高斯项处理，从而在反演所得PSD的大粒径处出现虚假峰。
在超低颗粒浓度DLS测量中，如何去除或减小光强ACF中非高斯项的影响，一直是提高反演结果准确性的关键。上世纪90年代，WILLEMSE A W等人[10-12]根据颗粒布朗运动和颗粒数量波动引起的散射光强信号的频率不同，在探测器和相关器之间增加一个低通滤波器，对信号进行高低频分离。虽然该方法在理论上可行，但会引入额外的噪声，且改变DLS实时自相关运算的工作模式。2021年，WANG Q等人[13]提出通过对光强ACF进行微分来识别和分离ACF中的数量波动项，并且在分离过程中对含噪ACF通过拟合进行平滑处理，从而改善了PSD的反演效果。同年，WANG M J等人[14]通过核函数重构直接建立了包含非高斯项的ACF与PSD之间的关系式，利用该关系式得到了理想的模拟数据反演结果。然而，实测数据反演结果与真实值相去甚远。产生这一现象的原因在于，实测（采样）时间远未达到计算位于ACF长延迟段的非高斯模型所需的信号采样时间，这一时间约为105 s [15]。不足的采样时间会导致光强ACF畸变，使得重构模型不能正确地反演出PSD。为有效地减少相关函数畸变的影响，WANG Q等人[16]在后续的研究中发现，调整聚焦激光束束腰半径这一参数可以改善拟合效果。据此提出，依据最优拟合效果确定的最佳束腰半径这一参数来修正实测数据的非高斯模型，即由采样时间不足导致的相关函数畸变可通过调整非高斯项中的参数来修正，再将修正的非高斯相关模型与核函数重构方法相结合得到与实测数据相匹配的核矩阵，从而得到了更为准确的PSD反演结果。
无论是去除光强ACF中的非高斯项还是进行核函数重构，均能解决光强ACF与电场ACF间不满足Siegert关系的问题。但在对两种方式的反演结果对比中发现，仅仅对非高斯项做简单的去除，常常不能得到最佳的粒度分布反演结果，光强ACF中的非高斯项在DLS反演中的作用有待做进一步的分析与研究。本文分别采用去除和保留非高斯项两种方法进行了不同超低颗粒浓度的DLS反演，计算了对应3种粒度分布宽度的非高斯项中粒度信息的含量。在此基础上，给出了去除和保留非高斯项两种方法反演不同分布宽度颗粒出现结果差异的原因。
1 理论与方法
1.1 DLS基本原理与散射体积中的数量波动
常规浓度下，散射光强的波动主要来自于颗粒的布朗运动。当散射光强满足高斯分布时，散射光强ACF与电场ACF满足Siegert关系[8]：
$$ {g^{\left( 2 \right)}}\left( \tau \right) = 1 + \beta {\left| {{g^{\left( 1 \right)}}\left( \tau \right)} \right|^2} $$ (1) 式中：τ为延迟时间；g(2)(τ)为光强ACF；g(1)(τ)为归一化电场ACF；β为相干因子。对于多分散颗粒：
$$ {g^{\left( 1 \right)}}\left( \tau \right) = \int_0^\infty {G\left( \Gamma \right)} \exp \left( { - \Gamma \tau } \right){\mathrm{d}}\Gamma $$ (2) 其中有：
$$ \Gamma = D{q^2},D = \frac{{{k_{\mathrm{B}}}T}}{{3\pi \eta d}},q = \frac{{4\pi {n_0}}}{{{\lambda _0}}}\sin \left( {\frac{\theta }{2}} \right) $$ (3) 式中：Γ为衰减线宽（s−1）；G(Γ)为其归一化分布函数，且满足$\int_0^\infty {G\left( \Gamma \right)} {\mathrm{d}}\Gamma = 1$；D为平移扩散系数，单位m2/s；q为散射波矢量的幅值，单位nm−1；kB为Boltzmann常数，单位J/K；T为绝对温度，单位K；η为分散介质的黏度系数，单位cP；d为颗粒直径，单位nm；n0为悬浮介质的折射率；λ0为入射光束在真空中的波长，单位nm；θ为散射角，单位（°）−1。
将式（3）代入式（2），并写成离散化形式：
$$ {g^{\left( 1 \right)}}\left( {{\tau _j}} \right) = \sum\limits_{i = 1}^M {\exp \left[ { - \frac{{16\pi n_0^2{k_{\mathrm{B}}}T{\tau _j}}}{{3\eta \lambda _0^2{d_i}}}{{\sin }^2}\left( {\frac{\theta }{2}} \right)} \right]} f\left( {{d_i}} \right) $$ (4) 式中：τ j为第j相关通道对应的延迟时间，其中1≤ j ≤ N，N为相关器的通道数；di （i=1，2，…，M）为颗粒直径；f(di)为离散的PSD，且满足$\displaystyle\sum\limits_{i = 1}^M {f\left( {{d_i}} \right) = 1} $。式（4）可简化为
$$ {{\boldsymbol{g}}^{\left( 1 \right)}} = {\boldsymbol{Af}} $$ (5) 式中：g(1)是由g(1)(τj)构成的N×1维的矢量；f是由离散PSD组成的向量，其元素是f(di)，维数为M×1；A是对应于电场ACF数据的核矩阵，其元素是$A\left( {j,i} \right) = \exp \left[ { - \dfrac{{16\pi n_0^2{k_{\mathrm{B}}}T{\tau _j}}}{{3\eta \lambda _0^2{d_i}}}{{\sin }^2}\left( {\dfrac{\theta }{2}} \right)} \right]$，维数为N×M。式（5）是一个属于第一类Fredholm积分方程的病态方程，采用约束Tikhonov正则化方法将式（5）的解转化为约束优化问题：
$$ {M^\alpha }\left( {{\boldsymbol{f}},{{\boldsymbol{g}}^{\left( 1 \right)}}} \right) = {\left\| {{\boldsymbol{Af}} - {{\boldsymbol{g}}^{\left( 1 \right)}}} \right\|^2} + \alpha {\left\| {{\boldsymbol{Lf}}} \right\|^2}{\text{ }}s.t.{\text{ }}{\boldsymbol{f}} \geqslant {\bf{0}} $$ (6) 式中：M，α，L，$ || \cdot || $和${\left\| {{\boldsymbol{Lf}}} \right\|^2}$分别是稳定泛函、正则化参数、正则化矩阵、欧式范数和惩罚因子。正则化参数α控制着解的精度和稳定性，通过L-曲线准则确定，正则化矩阵选择二阶差分矩阵，求解式（6）即可得到PSD。
超低颗粒浓度条件下，光强ACF与电场ACF间的关系为[17]
$$ {g^{\left( 2 \right)}}\left( \tau \right) = 1 + \beta \exp \left( { - 2D{q^2}\tau } \right) + \frac{\gamma }{{\left\langle N \right\rangle }}{\left( {1 + \frac{{4D\tau }}{{\omega _0^2}}} \right)^{ - 1}}{\left( {1 + \frac{{4D\tau }}{{{a^2}}}} \right)^{ - 1/2}} $$ (7) 式中：γ=2−3/2可以用来表征高斯函数平方运算导致的有效散射体积的衰减程度[18]；〈N〉为表征颗粒数量浓度的散射体积内的平均颗粒数；ω0是聚焦光束的束腰半径；a为探测器接收孔半径。式（7）中右侧第2项反映了由布朗运动引起的散射场相位差的变化，称为高斯项。第3项则反映了颗粒进出散射体积引起的数量波动对光强ACF的影响，称为非高斯项。当散射体积中的平均颗粒数〈N〉< 100时，该非高斯项不可忽略[18]。非高斯项的存在，导致电场ACF无法通过光强ACF直接求取，因而成为超低颗粒浓度DLS测量中PSD准确反演的制约因素。
1.2 超低浓度DLS反演方法
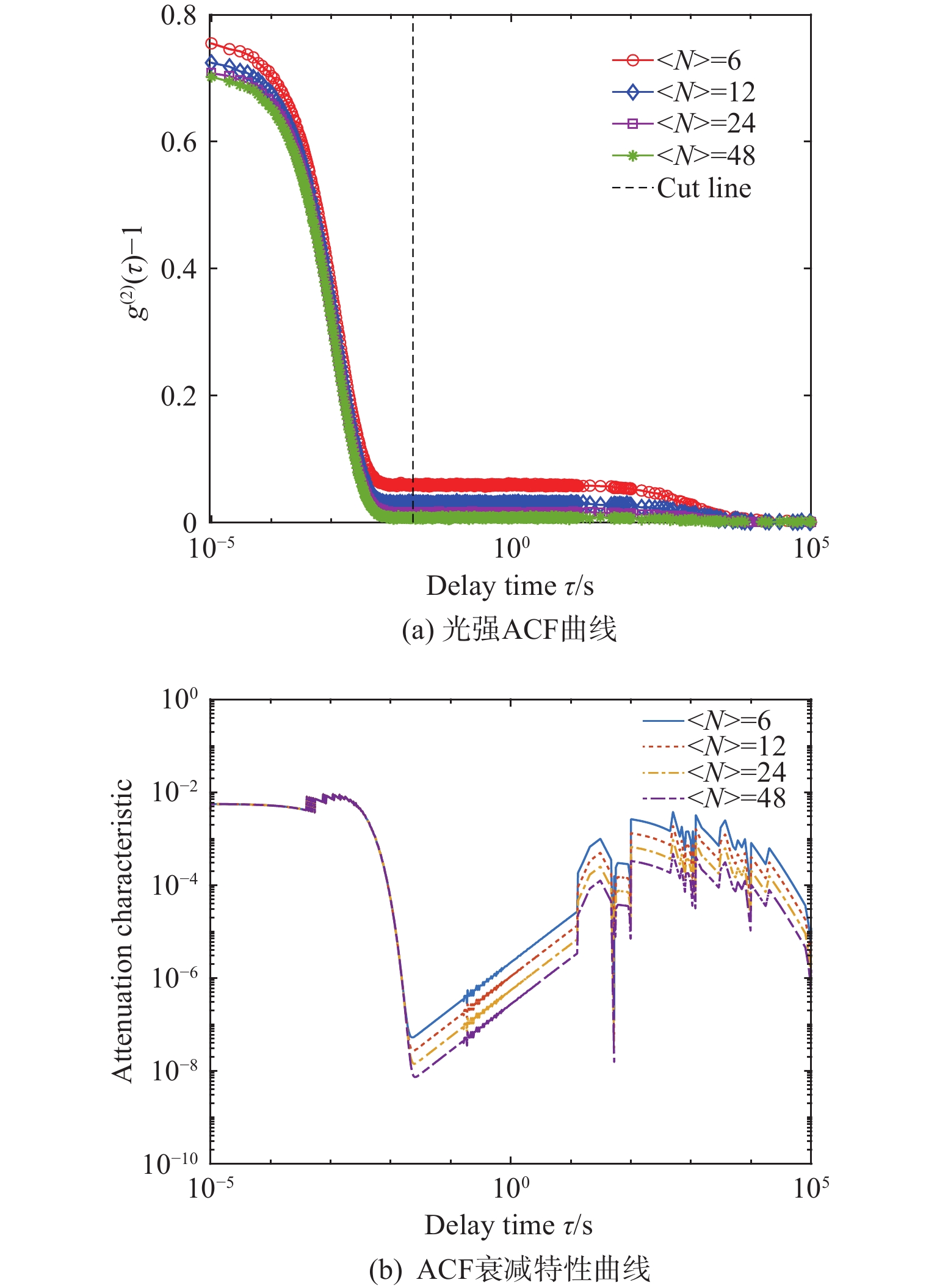
在超低浓度条件下，光强ACF由高斯项和非高斯项两部分组成，消除非高斯项对反演结果的影响，可以通过去除或保留非高斯项两种方式实现。去除非高斯项方法，需通过对光强ACF微分得到衰减特性曲线来确定高斯项与非高斯项的分界点，进而去除光强ACF中的非高斯项[13]。以600 nm单峰颗粒为例给出的光强ACF中，非高斯项的去除过程如图1所示。图1（b）为光强ACF的衰减特性曲线，是通过对图1（a）中ACF曲线的微分得到的，在衰减特性曲线最小值处截断即可去除非高斯项，使光强ACF与电场ACF满足Siegert关系式，从而可通过式（6）得到PSD。
![]()
图 1 600 nm单峰颗粒在不同浓度下的光强ACF曲线和ACF衰减特性曲线Figure 1. Light intensity ACF and ACF attenuation characteristic curves of 600 nm unimodal particles at different concentrations保留非高斯项法则是通过构造包含高斯项与非高斯项的电场ACF重构核矩阵，再采用Levenberg-Marquardt算法对实测ACF数据进行非线性最小二乘曲线拟合，用得到的最佳束腰半径ω0修正重构的核矩阵[16]。
通过类比Siegert方程，将式（7）的离散形式定义为等效电场ACF：
$$ {g_1}\left( {{\tau _j}} \right) = \sum\limits_{i = 1}^M {\sqrt {{A_1}\left( {{\tau _j},{d_i}} \right) + {A_2}\left( {{\tau _j},{d_i}} \right)} f\left( {{d_i}} \right)} $$ (8) 其中有：
$$ {A_1}\left( {{\tau _j},{d_i}} \right) = \exp \left( { - \frac{{32\pi n_0^2{k_{\mathrm{B}}}T{\tau _j}}}{{3\eta \lambda _0^2{d_i}}}{{\sin }^2}\left( {\frac{\theta }{2}} \right)} \right)$$ (9) $$ {A_2}\left( {{\tau _j},{d_i}} \right) = \frac{\gamma }{{\beta \left\langle N \right\rangle }}{\left( {1 + \frac{{4{k_{\mathrm{B}}}T{\tau _j}}}{{3\pi \eta {d_i}\omega _0^2}}} \right)^{ - 1}}{\left( {1 + \frac{{4{k_{\mathrm{B}}}T{\tau _j}}}{{3\pi \eta {d_i}{a^2}}}} \right)^{ - {1}/{2}}} $$ (10) 对重构的核矩阵则有：
$$ {{\boldsymbol{A}}_r} = \sqrt {{{\boldsymbol{A}}_1} + {{\boldsymbol{A}}_2}} $$ (11) 修正后代入式（6），即可求得PSD。
2 模拟数据反演
2.1 模拟实验参数及条件
为了分析超低颗粒浓度DLS反演中非高斯项的作用，分别采用去除非高斯项（non-Gaussian term separation, NGS）方法和保留非高斯项的核函数重构（kernel function reconstruction, KFR）方法对不同分布宽度的单峰颗粒的光强ACF数据进行反演。模拟的PSD采用Johnson's SB函数[19]：
$$ \begin{split} f\left( d \right) =& \frac{\sigma }{{\left( {{d_{\max }} - {d_{\min }}} \right)\sqrt {2\pi } }}{\left[ {t\left( {1 - t} \right)} \right]^{ - 1}}{\text{ }} \times \\ &\exp \left\{ { - 0.5{{\left[ {\mu + \sigma \ln \left( {\frac{t}{{1 - t}}} \right)} \right]}^2}} \right\} \end{split} $$ (12) 式中：dmax、dmin分别表示最大、最小颗粒粒径；$t = \dfrac{{d - {d_{\min }}}}{{{d_{\max }} - {d_{\min }}}}$是归一化颗粒粒径；μ和σ是分布参数，通过调整各个参数，能够模拟各种粒径分布。所有模拟实验对应的实验参数为：λ0=532 nm，ω0=54 μm，a=200 μm，T=298.15 K，n0=1.331 6，θ=90°，kB=1.380 7×10−23 J/K，η=0.89×10−3 cP，β=0.7，选取PSD的离散点数为M=300，散射体积中平均颗粒数〈N〉= 12、24和48。为与实际测量情况相符合，在模拟光强ACF数据g(2) (τ)中加入随机噪声：
$$ g_{{\mathrm{noise}}}^{\left( 2 \right)}\left( \tau \right) = {g^{\left( 2 \right)}}\left( \tau \right) + \delta n\left( \tau \right) $$ (13) 式中：n(τ)为高斯随机噪声；δ为噪声水平。
为评估反演效果，引入性能指标−峰值位置相对误差（Ep）和分布误差（V）：
$$ {E_{\mathrm{p}}} = \frac{{\left| {{P_{{\mathrm{meas}}}} - {P_{{\mathrm{true}}}}} \right|}}{{{P_{{\mathrm{true}}}}}} $$ (14) $$ V = {\left\{ {\left( {{{\sum\limits_{i = 1}^M {\left[ {{f_{{\mathrm{true}}}}\left( {{d_i}} \right) - {f_{{\mathrm{meas}}}}\left( {{d_i}} \right)} \right]}^2 }}} \right)/M} \right\}^{\tfrac{1}{2}}} $$ (15) 式中：Pmeas表示反演得到的峰值粒径；Ptrue表示真实峰值粒径；ftrue(di)表示真实的PSD；fmeas(di)表示反演的PSD。
2.2 模拟数据反演
2.2.1 不同分布宽度的颗粒粒度模拟反演与结果分析
在模拟实验中，选取了3组不同分布宽度的单峰颗粒，表1为模拟PSD的分布参数和特性。
表 1 模拟PSD的参数和特性Table 1. Parameters and properties of simulated PSDsPtrue/nm PSD width type μ σ (dmin, dmax) /nm Coefficient of
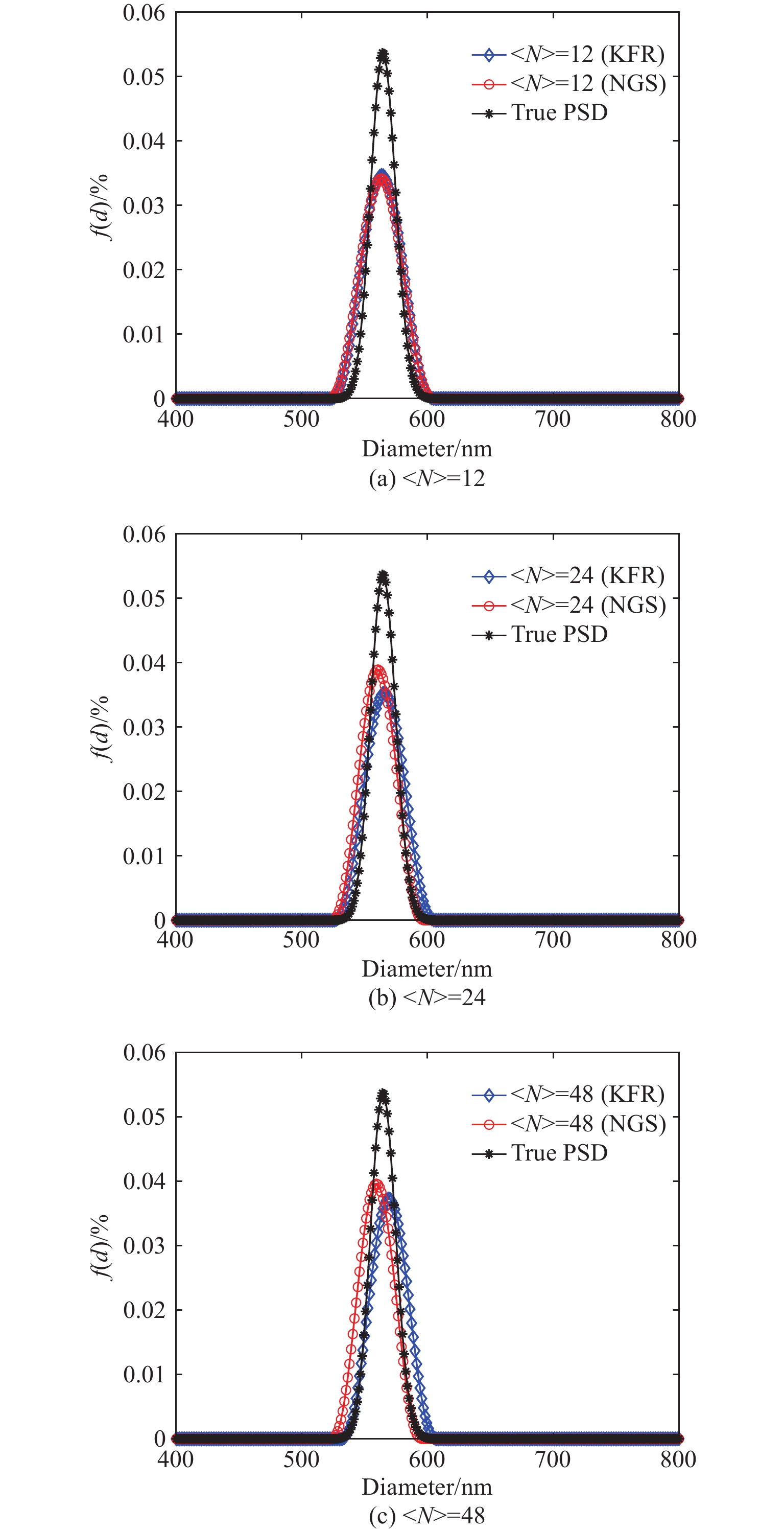
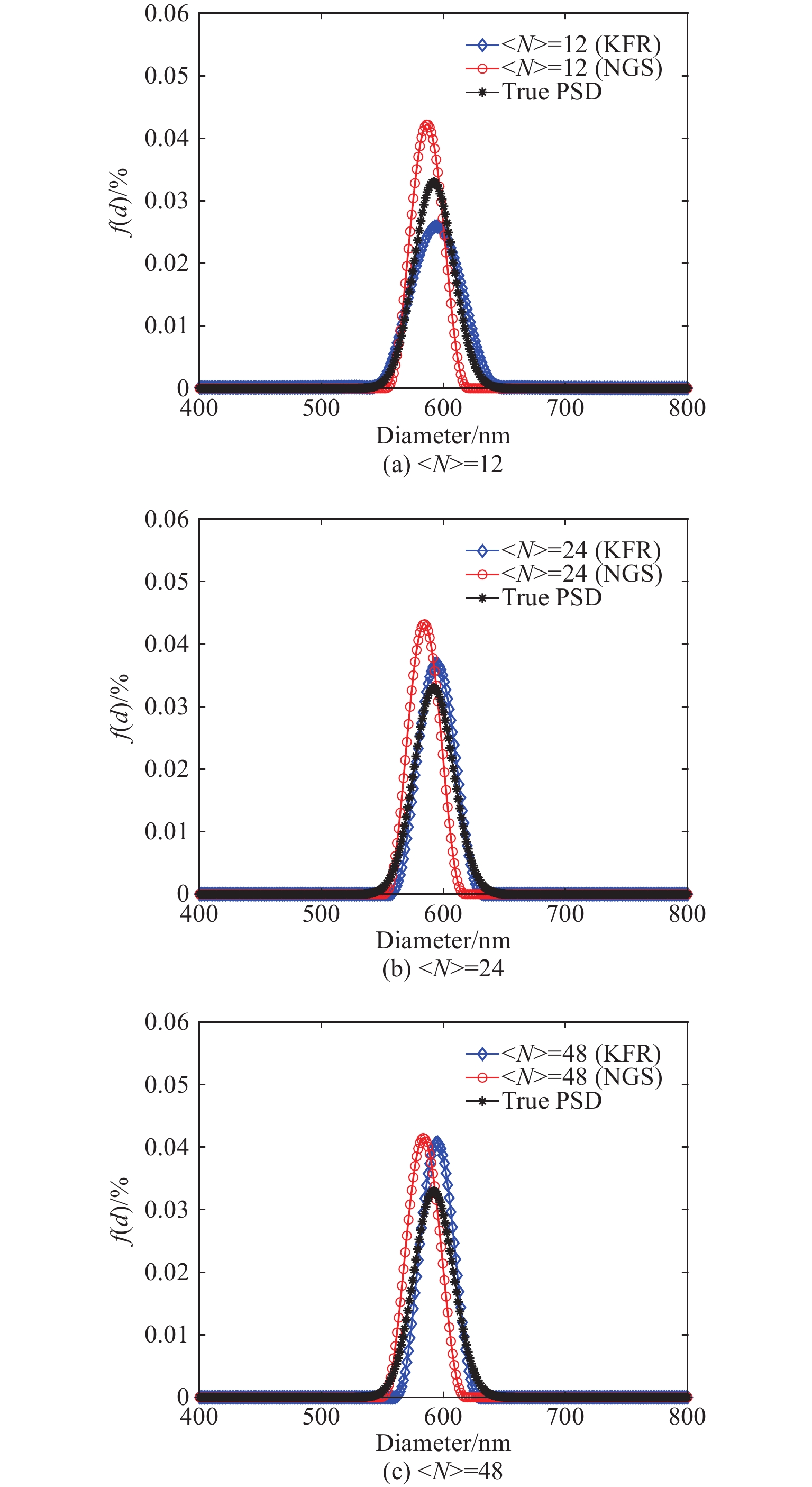
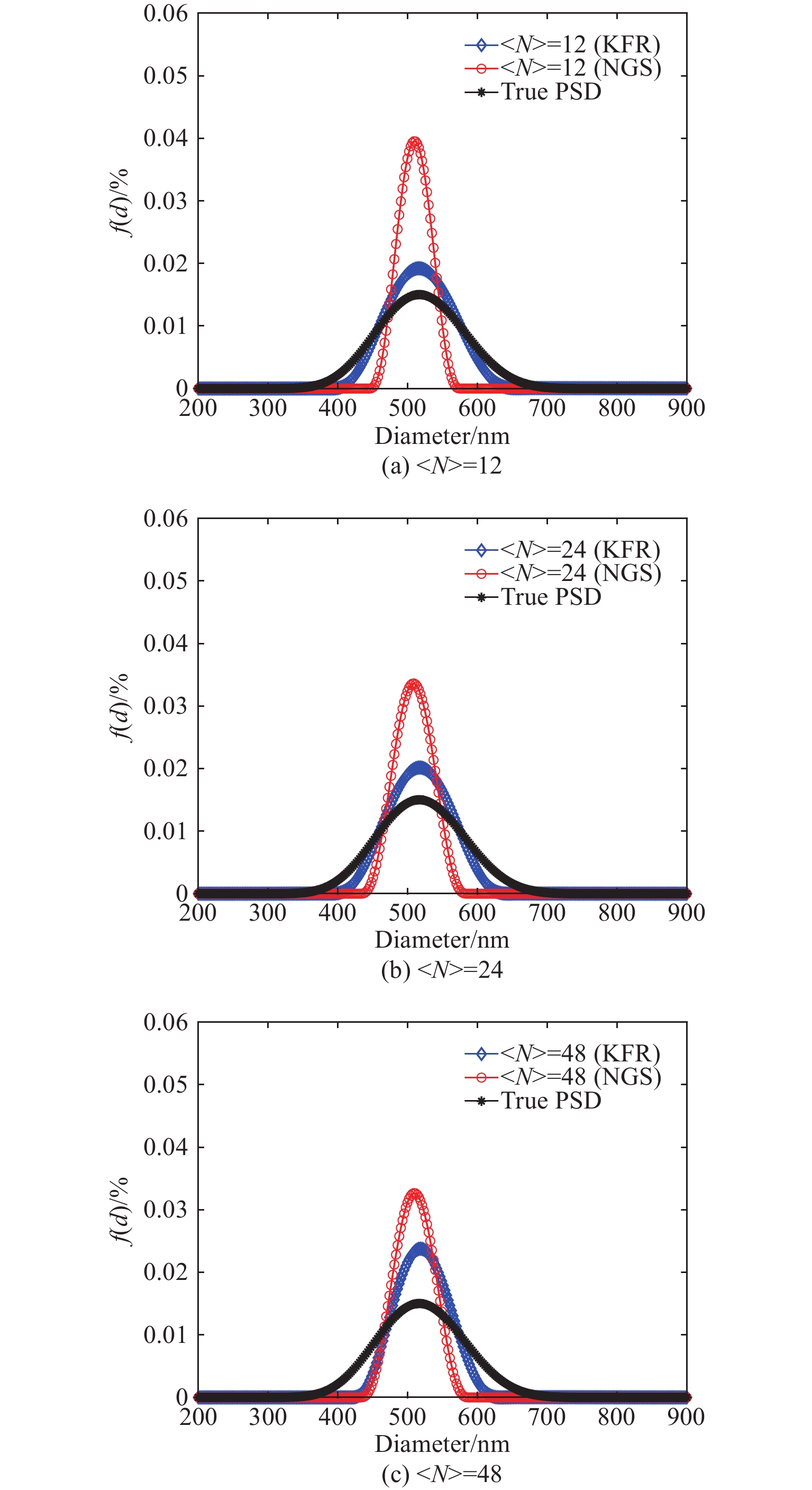
variation/%564 Narrow 3.5 9.8 (400, 800) 1.76 592 Medium 0.5 6.2 (400, 800) 2.70 517 Wide 0.5 2.8 (200, 900) 11.62 在〈N〉=12、24、48条件下，图2～图4以及表2为564 nm、592 nm和517 nm这3组颗粒采用两种方法的反演结果及相应的性能指标，图中f(d)为颗粒粒度分布占比，“True PSD”表示真实的粒度分布，模拟实验的噪声水平设定为5×10−3。
![]()
图 2 采用NGS方法和KFR方法在不同浓度下反演564 nm单峰窄分布颗粒所得的PSDFigure 2. Recovered PSD of inverting 564 nm unimodal narrow distribution particles by using NGS and KFR methods at different concentrations![]()
图 3 采用NGS方法和KFR方法在不同浓度下反演592 nm单峰中等分布颗粒所得的PSDFigure 3. Recovered PSD of inverting 592 nm unimodal medium distribution particles by using NGS and KFR methods at different concentrations![]()
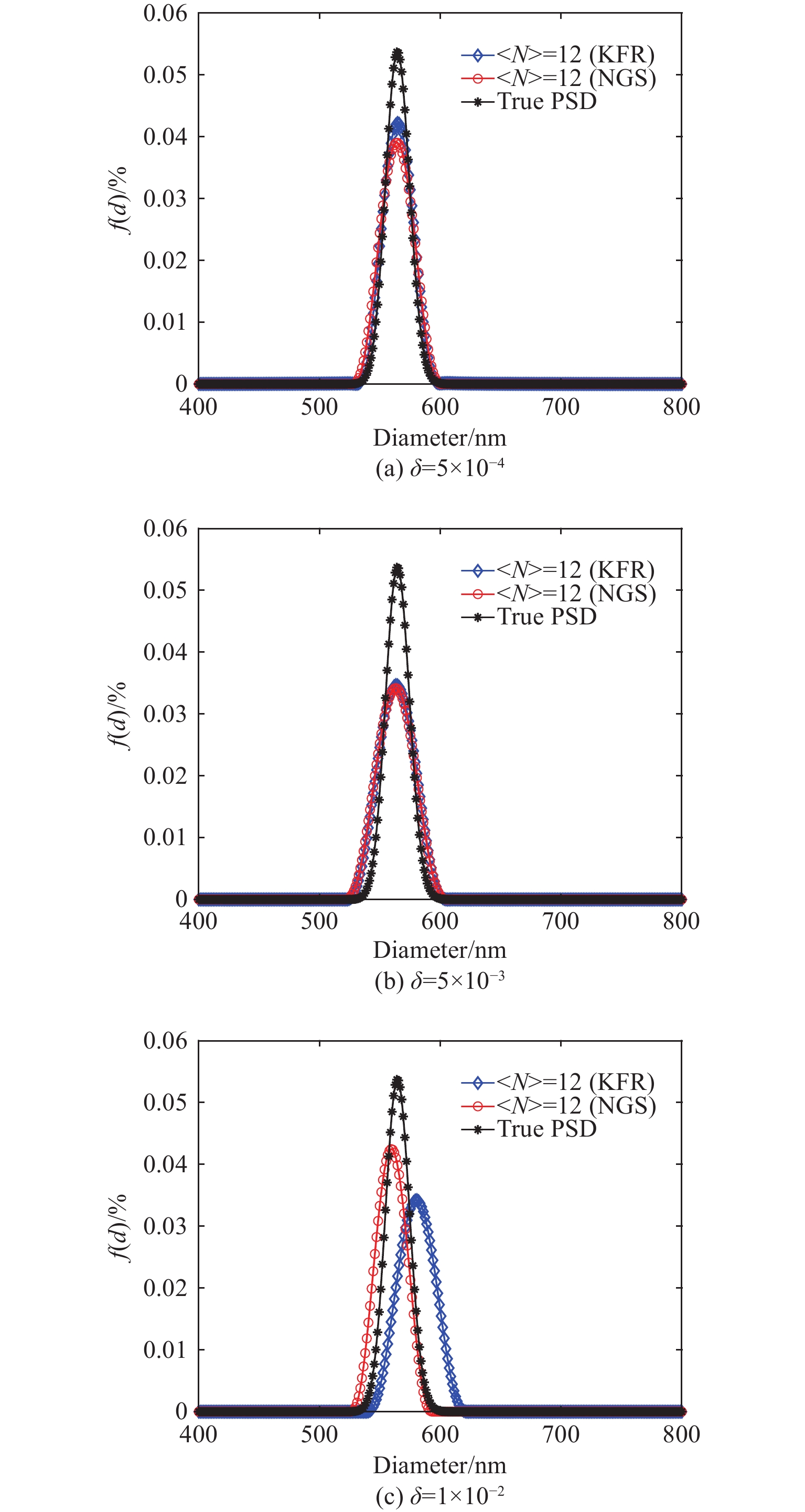
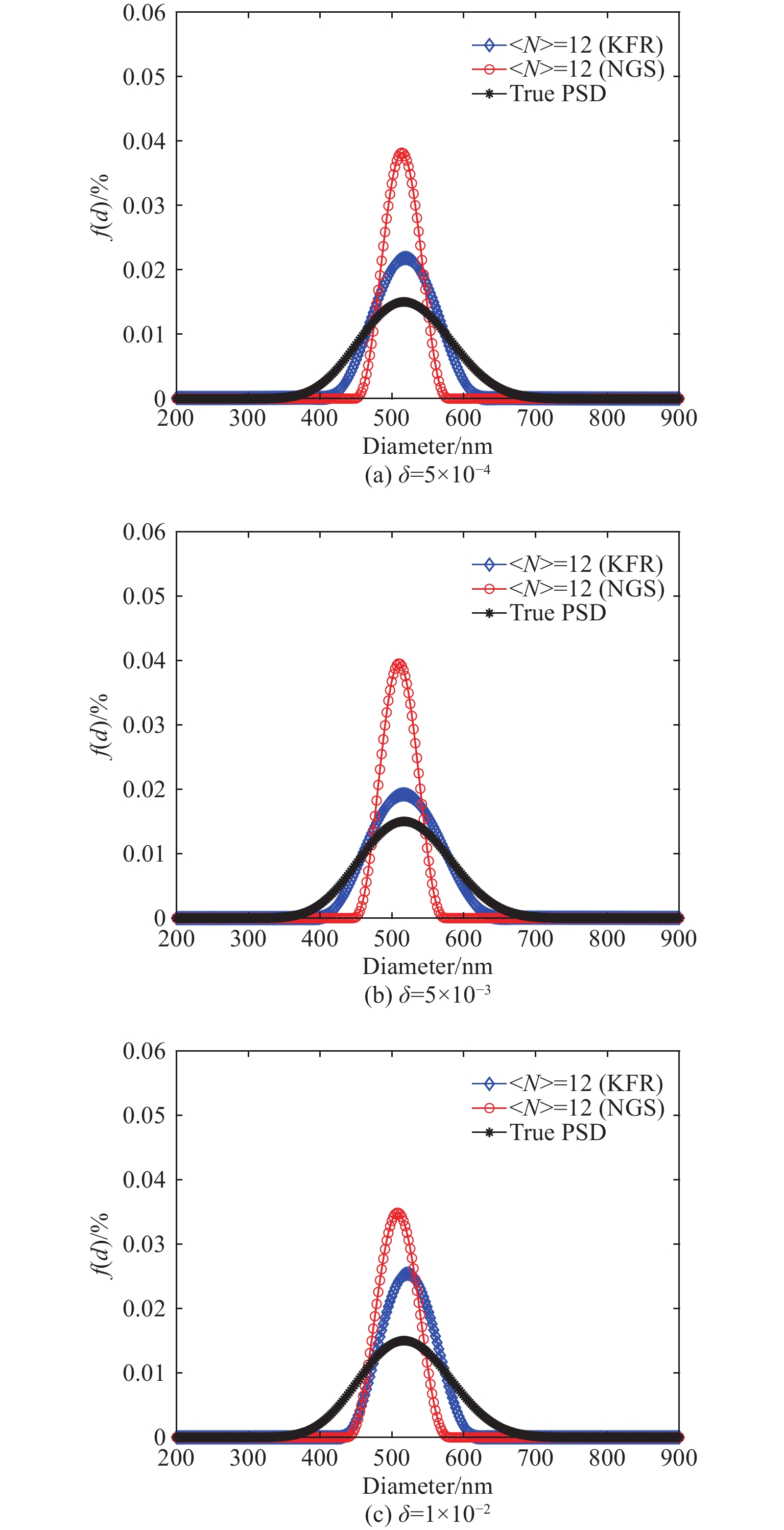
图 4 采用NGS方法和KFR方法在不同浓度下反演517 nm单峰宽分布颗粒所得的PSDFigure 4. Recovered PSD of inverting 517 nm unimodal wide distribution particles by using NGS and KFR methods at different concentrations表 2 采用NGS方法和KFR方法反演564 nm、592 nm和517 nm颗粒所得PSD的性能指标Table 2. Performance indices for PSD of inverting 564 nm, 592 nm and 517 nm particles by using NGS and KFR methodsPSD width type Ptrue/nm 〈N〉 NGS KFR Pmeas/nm Ep/% V/% Pmeas/nm Ep/% V/% Narrow 564 12 563 0.18 0.41 563 0.18 0.39 24 559 0.89 0.48 566 0.35 0.36 48 559 0.89 0.45 569 0.87 0.39 Medium 592 12 586 1.01 0.36 594 0.34 0.17 24 585 1.18 0.46 594 0.34 0.14 48 583 1.52 0.46 595 0.51 0.22 Wide 517 12 509 1.55 0.64 516 0.19 0.16 24 509 1.55 0.53 518 0.19 0.18 48 509 1.55 0.50 518 0.19 0.29 从图2～图4以及表2可以看出，除了〈N〉=12时，KFR方法对564 nm颗粒的峰值位置误差反演结果与NGS方法相同之外，在设定的3种颗粒浓度下，KFR方法对3种不同分布宽度的颗粒反演的峰值位置误差和分布误差均低于NGS方法。在相同颗粒浓度条件下，两种方法对窄分布颗粒的反演结果没有明显差别。但随着粒径分布宽度的增大，NGS方法反演结果的峰值位置误差明显相应增大，而KFR方法的峰值位置误差则无明显变化。
2.2.2 不同噪声水平的颗粒粒度模拟反演与结果分析
选取〈N〉=12的564 nm单峰窄分布和517 nm单峰宽分布颗粒，噪声水平分别设定为5×10−4、5×10−3和1×10−2，反演的PSD如图5和图6所示，表3为相应的性能指标。
![]()
图 5 采用NGS方法和KFR方法在不同噪声水平下反演564 nm单峰窄分布颗粒所得的PSDFigure 5. Recovered PSD of inverting 564 nm unimodal narrow distribution particles by using NGS and KFR methods at different noise levels![]()
图 6 采用NGS方法和KFR方法在不同噪声水平下反演517 nm单峰宽分布颗粒所得的PSDFigure 6. Recovered PSD of inverting 517 nm unimodal wide distribution particles by using NGS and KFR methods at different noise levels表 3 采用NGS方法和KFR方法反演564 nm和517 nm颗粒在不同噪声水平下所得的PSD的性能指标Table 3. Performance indices for recovered PSD of inverting 564 nm and 517 nm particles by using NGS and KFR methods at different noise levelsPSD width type Ptrue/nm δ NGS KFR Pmeas/nm Ep/% V/% Pmeas/nm Ep/% V/% Narrow 564 5×10−4 565 0.18 0.29 565 0.18 0.22 5×10−3 563 0.18 0.41 563 0.18 0.39 1×10−2 559 0.89 0.43 581 3.01 0.83 Wide 517 5×10−4 514 0.58 0.61 518 0.19 0.23 5×10−3 509 1.55 0.64 516 0.19 0.16 1×10−2 509 1.55 0.55 521 0.77 0.33 从图5～图6以及表3可以看出，在较低噪声水平（5×10−4和5×10−3）下，NGS和KFR两种方法对窄分布颗粒反演结果的峰值位置误差和分布误差无明显差别。当噪声水平增加到1×10−2时，NGS方法反演结果的峰值位置误差和分布误差明显低于KFR方法。对于低浓度的宽分布颗粒，在所有噪声水平下，KFR方法反演结果的峰值位置误差和分布误差均低于NGS方法。
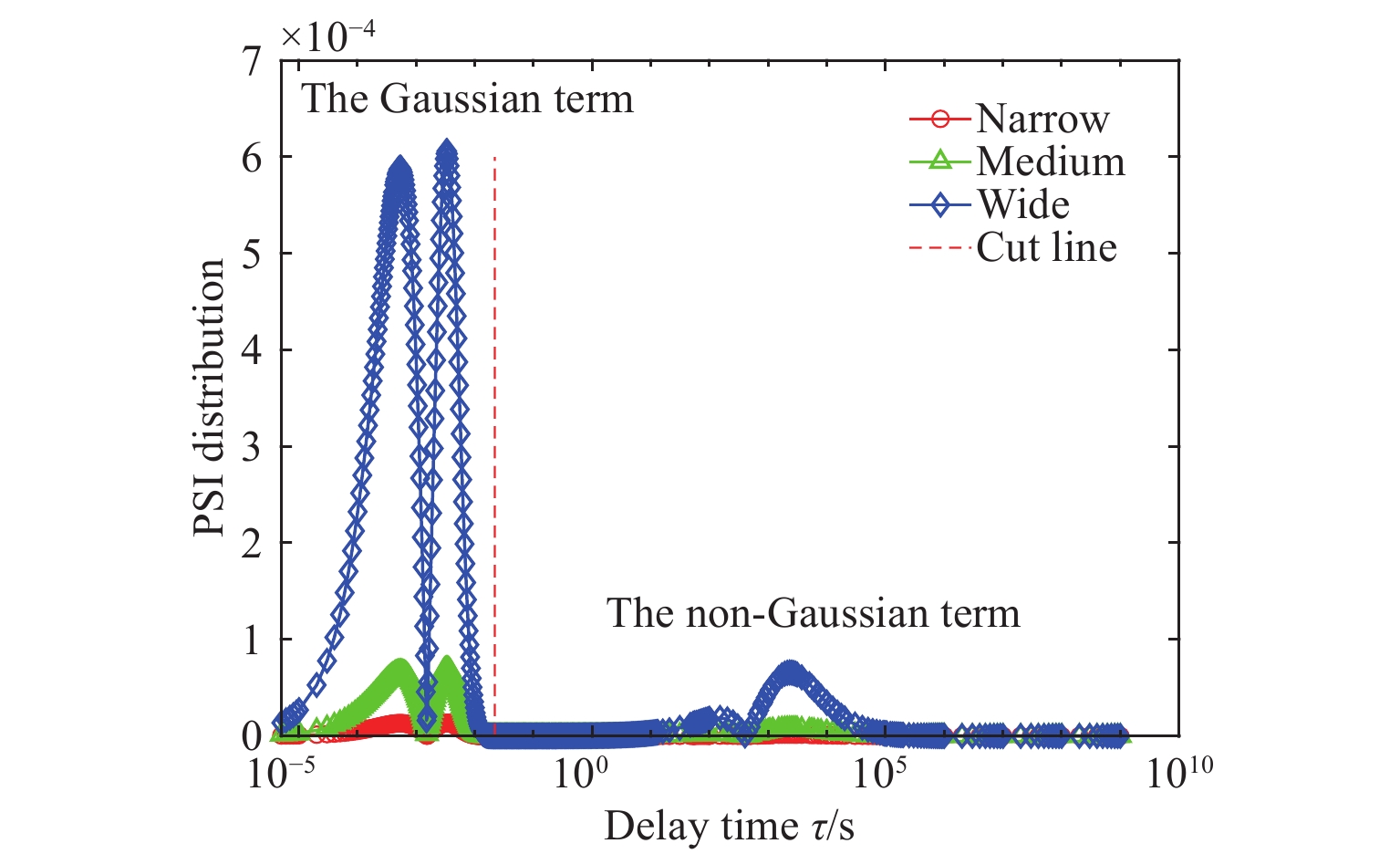
从模拟数据的反演结果可以看出，对于窄分布颗粒，在高噪声条件下，NGS方法能够给出优于KFR方法的PSD反演结果；而在较低噪声条件下，两种方法反演结果的性能指标并无明显差别。对于宽分布颗粒，KFR方法在各种噪声条件下所得反演结果的性能指标均优于NGS方法。为分析超低颗粒浓度DLS反演中非高斯项的作用，采用模拟的光强ACF和与之对应颗粒的平均粒径重构的光强ACF作差值的方法[20]，计算了564 nm单峰颗粒体系在3种不同分布宽度下的颗粒粒度信息（particle size information, PSI）在光强ACF中的分布，如图7所示。
![]()
图 7 不同分布宽度下的564nm单峰颗粒体系在对应的ACF中的PSI分布Figure 7. PSI distribution of 564 nm unimodal particle systems in corresponding ACF with different distribution widths图7中，“Cut line”为高斯项与非高斯项的分界线，“Narrow”表示窄分布颗粒，“Wide”表示宽分布颗粒，“Medium”表示中等分布宽度的颗粒。可以看出，随着粒度分布的增宽，非高斯项中所含的PSI显著增加，可见宽分布颗粒光强ACF的非高斯项中包含更多的PSI。这也解释了非高斯项对宽分布颗粒反演的意义，即保留非高斯项的ACF可以提供更多的PSI，从而可以给出更为准确的PSD反演结果。由于窄分布颗粒对应非高斯项中包含的PSI少，在噪声影响较小的情况下，保留或去除非高斯项对粒度反演没有明显影响；但在信号噪声较大时，保留非高斯项则会因增加数据中的噪声而导致反演结果变差。
3 实测数据反演
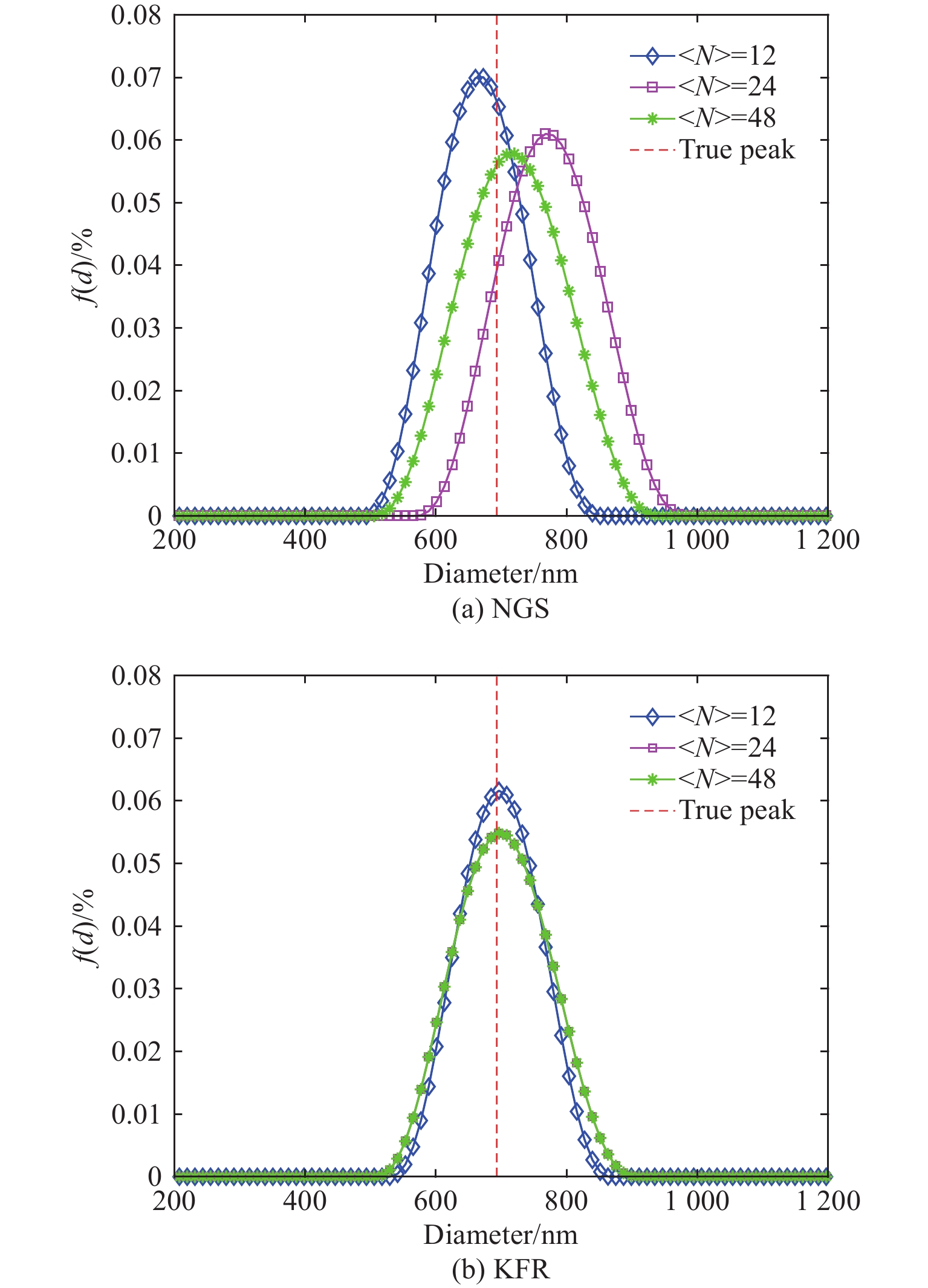
实测数据取自作者所在实验室的DLS测量实验平台，实验装置的主要部分包括一个波长532 nm的固体激光器（MGL-III-532 nm-15 mW）、一个光子计数器（CH326, Hamamatsu Photonics）和一个自行研制的512通道的数字相关器。被测样品采用平均粒径分别为（203±5）nm（Duke Scientific, 3200A）和（693±10） nm（GBW(E)120087）的标准聚苯乙烯乳胶球颗粒，相应的变异系数分别为2.3%和2.9%，体积分数分别为1.05%和0.315%，通过蒸馏水稀释后得到表4所示的颗粒数量浓度。此外测量角度为90°，测量时间为120 s，样品温度为298.15 K，入射透镜焦距为175 mm，探测器接收孔径为400 μm。
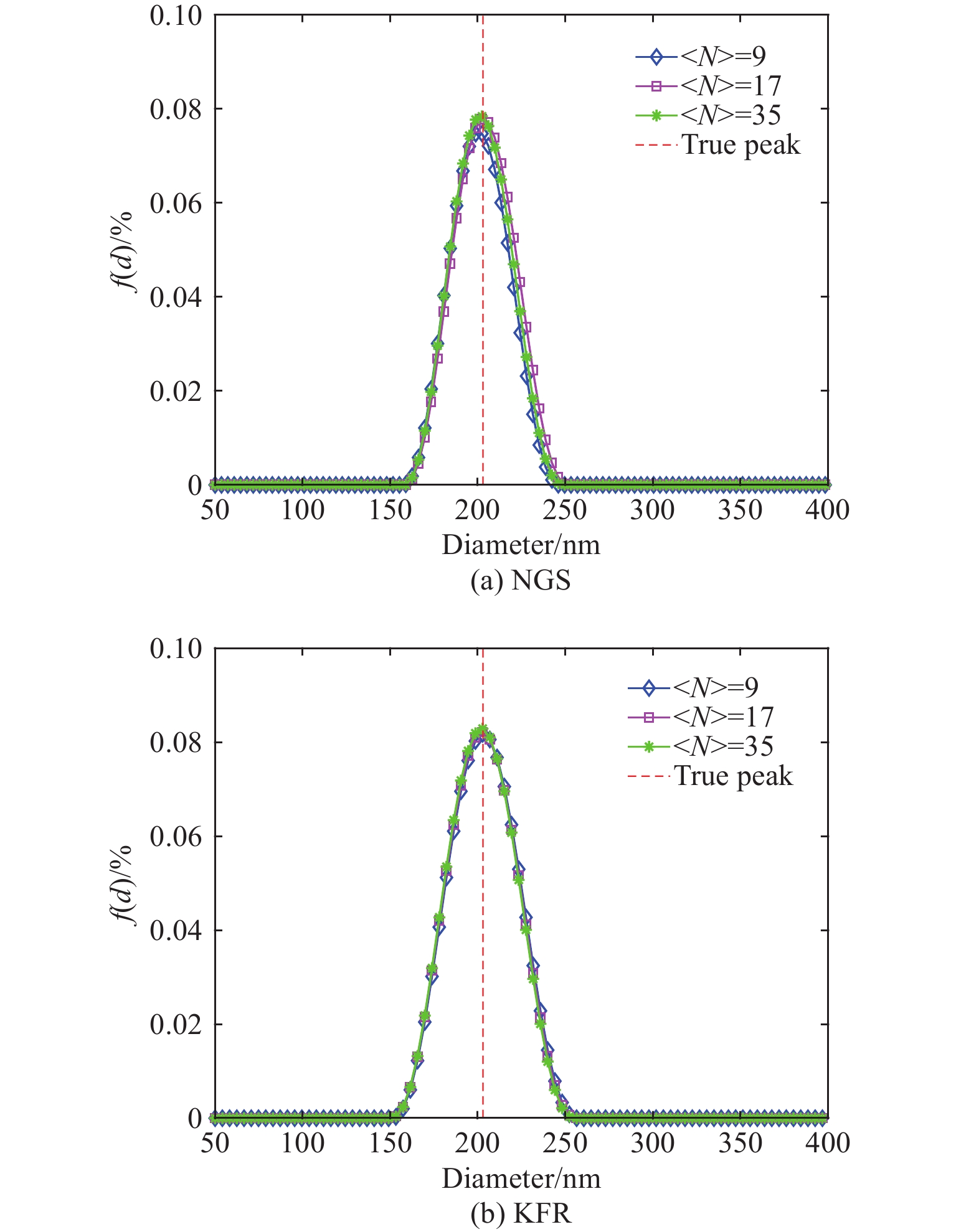
表 4 样品的体积分数及相应的颗粒数Table 4. Volume fraction and corresponding particle number of two series samplesDiameter/nm Coefficient of variation/% Volume fraction 〈N〉 203 2.3 3.2×10−8 9 6.3×10−8 17 1.3×10−7 35 693 2.9 1.7×10−6 12 3.6×10−6 24 7.3×10−6 48 NGS和KFR两种方法的反演结果如图8和图9所示，图中“True peak”表示真实PSD的峰值位置，表5为相应的性能指标。可以看出，对于203 nm样品颗粒，两种方法的反演结果没有明显差别。对于693 nm样品颗粒，KFR方法反演结果的峰值位置误差明显低于NGS方法。对照模拟数据的反演结果可以发现，尽管实测样品均采用了标准颗粒，但二者的变异系数并不一样，203 nm样品颗粒的变异系数为2.3%，位于模拟数据的窄分布范围，和窄分布反演结果的结论一致。693 nm样品颗粒的变异系数为2.9%，在模拟数据的中等分布宽度范围，和中等分布反演结果的结论一致。
![]()
图 8 采用NGS和KFR两种方法反演203 nm颗粒所得的PSDFigure 8. Recovered PSD of inverting 203 nm particles by using NGS and KFR methods![]()
图 9 采用NGS和KFR两种方法反演693 nm颗粒所得的PSDFigure 9. Recovered PSD of inverting 693 nm particles by using NGS and KFR methods表 5 采用NGS方法和KFR方法反演203 nm和693 nm颗粒所得PSD的性能指标Table 5. Performance indices for recovered PSD of inverting 203 nm and 693 nm particles by using NGS and KFR methodsPtrue/nm 〈N〉 NGS KFR Pmeas/nm Ep/% Pmeas/nm Ep/% 203 9 202 0.49 203 0 17 202 0.49 203 0 35 202 0.49 203 0 693 12 672 3.03 696 0.43 24 768 10.82 696 0.43 48 720 3.90 696 0.43 4 结论
在超低浓度DLS测量中，对光强ACF中非高斯项的不同处理方式会影响反演结果的准确性，这种影响与被测颗粒PSD的宽度有关。对于窄分布颗粒体系，在较低噪声水平下，去除与保留非高斯项对粒度反演无明显影响。随着噪声水平的增高，去除非高斯项方法反演结果的性能指标优于保留非高斯项方法。但对于宽分布颗粒体系，保留非高斯项则可以得到更为准确的反演结果。产生这一结果的原因在于，不同宽度PSD对应的光强ACF中非高斯项的粒度信息含量不同。与窄分布颗粒体系相比，宽分布颗粒对应的光强ACF中的非高斯项含有更多的粒度信息，去除非高斯项会导致粒度信息的丢失，从而降低反演结果的准确性。因此，对于超低浓度的宽分布颗粒体系，为保证DLS测量结果的准确性，进行PSD反演时应保留非高斯项。由于光强ACF的长延迟时段含有较多噪声，对于窄分布颗粒体系，保留非高斯项不会使反演受益，反而在信号噪声水平较高时，还会降低反演结果的准确性。
-
![]()
图 1 600 nm单峰颗粒在不同浓度下的光强ACF曲线和ACF衰减特性曲线
Figure 1. Light intensity ACF and ACF attenuation characteristic curves of 600 nm unimodal particles at different concentrations
![]()
图 2 采用NGS方法和KFR方法在不同浓度下反演564 nm单峰窄分布颗粒所得的PSD
Figure 2. Recovered PSD of inverting 564 nm unimodal narrow distribution particles by using NGS and KFR methods at different concentrations
![]()
图 3 采用NGS方法和KFR方法在不同浓度下反演592 nm单峰中等分布颗粒所得的PSD
Figure 3. Recovered PSD of inverting 592 nm unimodal medium distribution particles by using NGS and KFR methods at different concentrations
![]()
图 4 采用NGS方法和KFR方法在不同浓度下反演517 nm单峰宽分布颗粒所得的PSD
Figure 4. Recovered PSD of inverting 517 nm unimodal wide distribution particles by using NGS and KFR methods at different concentrations
![]()
图 5 采用NGS方法和KFR方法在不同噪声水平下反演564 nm单峰窄分布颗粒所得的PSD
Figure 5. Recovered PSD of inverting 564 nm unimodal narrow distribution particles by using NGS and KFR methods at different noise levels
![]()
图 6 采用NGS方法和KFR方法在不同噪声水平下反演517 nm单峰宽分布颗粒所得的PSD
Figure 6. Recovered PSD of inverting 517 nm unimodal wide distribution particles by using NGS and KFR methods at different noise levels
![]()
图 7 不同分布宽度下的564nm单峰颗粒体系在对应的ACF中的PSI分布
Figure 7. PSI distribution of 564 nm unimodal particle systems in corresponding ACF with different distribution widths
![]()
图 8 采用NGS和KFR两种方法反演203 nm颗粒所得的PSD
Figure 8. Recovered PSD of inverting 203 nm particles by using NGS and KFR methods
![]()
图 9 采用NGS和KFR两种方法反演693 nm颗粒所得的PSD
Figure 9. Recovered PSD of inverting 693 nm particles by using NGS and KFR methods
表 1 模拟PSD的参数和特性
Table 1 Parameters and properties of simulated PSDs
Ptrue/nm PSD width type μ σ (dmin, dmax) /nm Coefficient of
variation/%564 Narrow 3.5 9.8 (400, 800) 1.76 592 Medium 0.5 6.2 (400, 800) 2.70 517 Wide 0.5 2.8 (200, 900) 11.62 
下载: 导出CSV
表 2 采用NGS方法和KFR方法反演564 nm、592 nm和517 nm颗粒所得PSD的性能指标
Table 2 Performance indices for PSD of inverting 564 nm, 592 nm and 517 nm particles by using NGS and KFR methods
PSD width type Ptrue/nm 〈N〉 NGS KFR Pmeas/nm Ep/% V/% Pmeas/nm Ep/% V/% Narrow 564 12 563 0.18 0.41 563 0.18 0.39 24 559 0.89 0.48 566 0.35 0.36 48 559 0.89 0.45 569 0.87 0.39 Medium 592 12 586 1.01 0.36 594 0.34 0.17 24 585 1.18 0.46 594 0.34 0.14 48 583 1.52 0.46 595 0.51 0.22 Wide 517 12 509 1.55 0.64 516 0.19 0.16 24 509 1.55 0.53 518 0.19 0.18 48 509 1.55 0.50 518 0.19 0.29
下载: 导出CSV
表 3 采用NGS方法和KFR方法反演564 nm和517 nm颗粒在不同噪声水平下所得的PSD的性能指标
Table 3 Performance indices for recovered PSD of inverting 564 nm and 517 nm particles by using NGS and KFR methods at different noise levels
PSD width type Ptrue/nm δ NGS KFR Pmeas/nm Ep/% V/% Pmeas/nm Ep/% V/% Narrow 564 5×10−4 565 0.18 0.29 565 0.18 0.22 5×10−3 563 0.18 0.41 563 0.18 0.39 1×10−2 559 0.89 0.43 581 3.01 0.83 Wide 517 5×10−4 514 0.58 0.61 518 0.19 0.23 5×10−3 509 1.55 0.64 516 0.19 0.16 1×10−2 509 1.55 0.55 521 0.77 0.33
下载: 导出CSV
表 4 样品的体积分数及相应的颗粒数
Table 4 Volume fraction and corresponding particle number of two series samples
Diameter/nm Coefficient of variation/% Volume fraction 〈N〉 203 2.3 3.2×10−8 9 6.3×10−8 17 1.3×10−7 35 693 2.9 1.7×10−6 12 3.6×10−6 24 7.3×10−6 48
下载: 导出CSV
表 5 采用NGS方法和KFR方法反演203 nm和693 nm颗粒所得PSD的性能指标
Table 5 Performance indices for recovered PSD of inverting 203 nm and 693 nm particles by using NGS and KFR methods
Ptrue/nm 〈N〉 NGS KFR Pmeas/nm Ep/% Pmeas/nm Ep/% 203 9 202 0.49 203 0 17 202 0.49 203 0 35 202 0.49 203 0 693 12 672 3.03 696 0.43 24 768 10.82 696 0.43 48 720 3.90 696 0.43
下载: 导出CSV
-
[1] PECORA R. Dynamic light scattering measurement of nanometer particles in liquids[J]. Journal of Nanoparticle Research, 2000, 2(2): 123-131. doi: 10.1023/A:1010067107182
[2] The International Organization for Standardization Technical Committees. Particle size analysis-dynamic light scattering (DLS): ISO 22412-2017[S]. Geneva: International Organization for Standardization, 2017.
[3] HOU J, CI H L, WANG P F, et al. Nanoparticle tracking analysis versus dynamic light scattering: case study on the effect of Ca2+ and alginate on the aggregation of cerium oxide nanoparticles[J]. Journal of Hazardous Materials, 2018, 360: 319-328. doi: 10.1016/j.jhazmat.2018.08.010
[4] ZHAN S N, HU J Q, LI Y, et al. Direct competitive ELISA enhanced by dynamic light scattering for the ultrasensitive detection of aflatoxin B1 in corn samples[J]. Food Chemistry, 2021, 342: 128327. doi: 10.1016/j.foodchem.2020.128327
[5] CARVALHO J W P, SANTIAGO P S, BATISTA T, et al. On the temperature stability of extracellular hemoglobin of Glossoscolex paulistus, at different oxidation states: SAXS and DLS studies[J]. Biophysical Chemistry, 2012, 163/164: 44-55. doi: 10.1016/j.bpc.2012.02.004
[6] BAI M X, CHAOLUMEN B, ASAI D, et al. Role of a long-chain alkyl group in sulfated alkyl oligosaccharides with high anti-HIV activity revealed by SPR and DLS[J]. Carbohydrate Polymers, 2020, 245: 116518. doi: 10.1016/j.carbpol.2020.116518
[7] 李丰果, 杨冠玲, 何振江. 动态光散射测量核壳双层纳米颗粒的研究[J]. 计量学报, 2005, 26(4): 368-371. LI Fengguo, YANG Guanling, HE Zhenjiang. A study on the measurement of core-shell nano-particles by dynamic light scattering[J]. Acta Metrologica Sinica, 2005, 26(4): 368-371.
[8] THOMAS J C. Photon correlation spectroscopy: technique and instrumentation[C]//SPIE Proceedings of Photon Correlation Spectroscopy: Multicomponent Systems. Los Angeles: SPIE, 1991, 1430: 2-18.
[9] SCHAEFER D W, BERNE B J. Light scattering from non-Gaussian concentration fluctuations[J]. Physical Review Letters, 1972, 28(8): 475-478. doi: 10.1103/PhysRevLett.28.475
[10] WILLEMSE A W, NIJMAN E J, MARIJNISSEN J C M, et al. Photon correlation spectroscopy–extending the limits of concentration[J]. KONA Powder and Particle Journal, 1998, 16: 102-115. doi: 10.14356/kona.1998013
[11] WILLEMSE A W, MARIJNISSEN J C M, VAN WUYCKHUYSE A L, et al. Low-concentration photon correlation spectroscopy[J]. Particle & Particle Systems Characterization, 1997, 14(4): 157-162.
[12] WILLEMSE A W, MARIJNISSEN J C M, WUYCKHUYSE A L, et al. Photon correlation spectroscopy for analysis of low concentration submicrometer samples[J]. Progress in Colloid & Polymer Science, 1997, 104(1): 113-116.
[13] WANG Q, SHEN J, WANG M J, et al. Measuring particle size in ultra-low concentration suspensions by removing the number fluctuation contribution in dynamic light scattering[J]. Optics Express, 2021, 29(23): 38567-38581. doi: 10.1364/OE.442698
[14] WANG M J, SHEN J, THOMAS J C, et al. Particle size measurement using dynamic light scattering at ultra-low concentration accounting for particle number fluctuations[J]. Materials, 2021, 14(19): 5683. doi: 10.3390/ma14195683
[15] NIJMAN E J, MERKUS H G, MARIJNISSEN J C M, et al. Investigation of the influence of low particle concentration on photon correlation spectroscopy[C]//Photon Correlation and Scattering. Washington: OSA, 2000: MB3.
[16] WANG Q, SHEN J, THOMAS J C, et al. Particle size distribution recovery from non-Gaussian intensity autocorrelation functions obtained from dynamic light scattering at ultra-low particle concentrations[J]. Powder Technology, 2023, 413: 118033. doi: 10.1016/j.powtec.2022.118033
[17] NIJMAN E J, MERKUS H G, MARIJNISSEN J C M, et al. Simulations and experiments on number fluctuations in photon-correlation spectroscopy at low particle concentrations[J]. Applied Optics, 2001, 40(24): 4058-4063. doi: 10.1364/AO.40.004058
[18] CHOWDHURY D P, SORENSEN C M, TAYLOR T W, et al. Application of photon correlation spectroscopy to flowing Brownian motion systems[J]. Applied Optics, 1984, 23(22): 4149. doi: 10.1364/AO.23.004149
[19] YU A B, STANDISH N. A study of particle size distributions[J]. Powder Technology, 1990, 62(2): 101-118. doi: 10.1016/0032-5910(90)80073-8
[20] 徐敏, 申晋, 黄钰, 等. 基于颗粒粒度信息分布特征的动态光散射加权反演[J]. 物理学报, 2018, 67(13): 293-307. doi: 10.7498/aps.67.20172377 XU Min, SHEN Jin, HUANG Yu, et al. Weighting inversion of dynamic light scattering based on particle-size information distribution character[J]. Acta Physica Sinica, 2018, 67(13): 293-307. doi: 10.7498/aps.67.20172377
-
期刊类型引用(6)
1. 孙茜，孙翠敏，黎晓伊. 基于多方向DTCWT和域自适应学习的遥感图像薄云去除. 湖南工业职业技术学院学报. 2023(04): 17-20+37 . 
百度学术
2. 李雪露，杨永辉，储茂祥，焦玉鹏. 一种改进的钢板表面缺陷图像增强算法. 激光杂志. 2022(07): 95-100 . 百度学术
3. 张玉，贾遂民. 噪声调节主成分变换下的遥感图像薄云去除. 测绘通报. 2021(03): 33-37 . 百度学术
4. 陈清江，石小涵，柴昱洲. 基于小波变换与卷积神经网络的图像去噪算法. 应用光学. 2020(02): 288-295 . 本站查看
5. 杨晓倩，贾振红，杨杰，Nikola KASABOV. 基于小波变换和Retinex结合的遥感图像的薄云去除. 激光杂志. 2019(10): 77-80 . 百度学术
6. 李华莹，林道玉，张捷，刘必欣. 基于生成对抗网络的遥感图像去云算法. 计算机与现代化. 2019(11): 13-17 . 百度学术
其他类型引用(6)
计量
- 文章访问数: 52
- HTML全文浏览量: 4
- PDF下载量: 43
- 被引次数: 12
陕公网安备 61011302001501号 