用于绝对相位恢复的鲁棒相位编码方法

朱浩杰; 汪宇; 梅芳芳; 周传起; 王宇杰; 侯文慧

doi:10.5768/JAO202445.0502004

用于绝对相位恢复的鲁棒相位编码方法

朱浩杰^1,,
汪宇¹,
梅芳芳¹,
周传起¹,
王宇杰¹,
侯文慧^{1, 2, 3, ,}

1.
安徽农业大学工学院，安徽合肥 230036
2.
安徽省智能农机装备工程实验室，安徽合肥 230036
3.
中科院合肥技术创新工程院，安徽合肥 230036

基金项目: 安徽省高校科研计划项目（2022AH050872）；电气传动与控制安徽省重点实验室开放基金资助项目（DQKJ202203）；安徽省研究生教育质量工程项目（2022xscx051）；新能源汽车暨智能网联汽车产业技术创新工程项目

详细信息

作者简介:
朱浩杰（1996—），男，硕士研究生，主要从事光学三维测量研究。E-mail：zhjand@stu.ahau.edu.cn

通讯作者:
侯文慧（1985—），女，博士，讲师，主要从事智慧农业研究。E-mail：hwh303@ahau.edu.cn

中图分类号: TN29
计量
- 文章访问数: 73
- HTML全文浏览量: 22
- PDF下载量: 30
出版历程
- 收稿日期: 2023-08-06
- 修回日期: 2023-09-14
- 网络出版日期: 2024-08-13
- 刊出日期: 2024-09-14

Robust phase-coding method for absolute phase retrieval

1.
College of Engineering, Anhui Agricultural University, Hefei 230036, China
2.
Anhui Province Engineering Laboratory of Intelligent Agricultural Machinery and Equipment, Hefei 230036, China
3.
Hefei Institute of Technology Innovation, Chinese Academy of Sciences, Hefei 230036, China

摘要

摘要:
相位编码方法已广泛用于条纹投影轮廓术（fringe projection profilometry, FPP）中的绝对相位恢复，然而FPP系统的gamma非线性严重影响了系统的鲁棒性和精度。从扭曲条纹图案中提取的包裹相位将偏离实际相位，不能直接用于恢复绝对相位。为解决这个问题，提出一种基于有效非线性校正策略的鲁棒相位编码方法。首先，通过相位直方图均衡（phase histogram equalization, PHE）方法调整失真的包裹相位，以获得校正的包裹相位。理论研究表明，非线性相位误差的频率是理想相位的3倍，因此提出使用相移直方图均衡（shifted-phase histogram equalization, SHE）方法进一步减小非线性相位误差。然后，通过Hermite插值算法拟合连续函数，减少SHE方法所引入的离散化误差。仿真和实验结果都表明，在gamma非线性情况下，所提方法比传统方法更具鲁棒性。
- 条纹投影轮廓术 /
- 相位展开 /
- gamma非线性 /
- 直方图均衡化 /
- 概率分布
Abstract:
Phase-coding method has been widely used for absolute phase retrieval in fringe projection profilometry (FPP). However, the robustness and the accuracy is severely affected by the gamma nonlinearity of FPP system. The wrapped phase extracted from distorted fringe patterns will deviate from the actual phase, which cannot be directly employed to retrieve the absolute phase. To address this problem, a robust phase-coding method based on an effective nonlinear correction strategy was proposed. First, the distorted wrapped phase could be adjusted by the phase histogram equalization (PHE) method to obtain the corrected wrapped phase. Theoretical studies demonstrated that the frequency of the nonlinear phase error is thrice that of the ideal phase. Therefore, the nonlinear phase error was further reduced by shifted-phase histogram equalization (SHE) method. Then, the continuous function was fitted by the Hermite interpolation algorithm, which could reduce the discretization error introduced by the SHE method. Both the simulation and experimental results show that the proposed method is more robust than the traditional method under gamma nonlinearity.
- fringe projection profilometry /
- phase unwrapping /
- gamma nonlinearity /
- histogram equalization /
- probability distribution

HTML全文

引言

结构光三维成像技术已广泛应用于工业设计、生物医学、建筑、文物保护等多个领域的三维测量^[1-3]。在多种结构光三维成像技术中，条纹投影轮廓术（FPP）因其非接触、高速和高分辨率而得到广泛应用^[4-6]。在FPP中，深度信息被编码到条纹图案的相位中，通过分析由物体表面调制的变形条纹图案可以提取相位分布^[7-9]。由于物体高度信息是从相位中计算得出的，因此相位的准确性对最终测量精度至关重要。

目前，相移轮廓术（phase-shifting profilometry, PSP）因其高可靠性、高分辨率、能够测量复杂物体等优点而成为相位提取的重要方法之一^[10-13]。考虑到PSP使用反正切函数进行相位提取，所得相位截断在0～2π的定义域范围内，具有2π不连续性，因此需要进行相位展开来消除不连续性以获得相位连续分布^[14-15]。目前已有多种相位展开算法，例如格雷编码法^[16]、相位编码法^[17]和多频相位展开法^[18]。具体而言，格雷编码法使用只有黑白编码图案，根据图像强度而不是其相位来确定条纹级次。鉴于相位可以比强度更好地传达信息，因此该方法对于测量复杂表面的鲁棒性较差^[17]。多频相位展开法通常采用低频条纹图案来展开高频条纹图案的包裹相位。投影的条纹图案数量会随着频率类型的增加而增加，导致测量效率低下。相比之下，相位编码法根据相位而不是强度将码字嵌入到条纹中。相位编码法对表面对比度、环境光和相机噪声不敏感，具有更好的鲁棒性。在相位编码方法中，可以通过将范围为（0，2π]的阶梯相位量化为K个阶梯高度为2π/K的相位来实现码字的嵌入，其中每个量化相位代表一个码字^[19]。然而，数字投影仪和相机的gamma非线性效应会在条纹图案的相位中引入非线性相位误差。非线性相位误差的存在严重降低了测量精度。为了克服此问题，ZHENG D等^[20]提出了一种新的相位编码方法，该方法使用6个附加的条纹图案来生成64个以上的唯一码字。虽然通过增加条纹图案的数量可以减少gamma非线性引起的非线性相位误差，但额外的条纹图案将牺牲测量速度。为此，WANG Y^[21]等提出了改进的相位编码方法，用于以更少的图案进行绝对相位展开。WANG L^[22]等提出了一种分段量化相位编码和解码方法，该方法可以在不减少相邻量化相位值之间的差异和不增加量化级别的情况下实现绝对相位展开。gamma非线性的影响可以在一定程度上减少。LIU K^[23]等提出了一种通用算法来校准器件非线性，以精确的预补偿条纹图案。CHEN H^[24]等提出了一种改进的基于希尔伯特变换的非线性校正方法。JE C^[25]等提出了一种相位直方图均衡方法，该方法直接对失真相位采用直方图均衡来恢复未失真相位。与低频正弦条纹投影相比，高频正弦条纹投影可以更好地还原物体的细节。但频率越高的正弦条纹投影也需要更多码字数量，这导致相邻量化相位值之间的差值将变得更小。因此，gamma非线性引起的相位误差会导致求解出的条纹级次产生错误，进而无法正确展开包裹相位。已经有研究证明相位误差的幅度限制了码字的最大数量，相位编码方法中的码字数量不能任意增加^[26]。因此，综上所述，如何有效消除gamma非线性的影响，成为一个迫切需要解决的问题。

本文基于有效的非线性校正策略，在不增加条纹图案的数量情况下，提出一种鲁棒相位编码方法来校正由gamma非线性引起的非线性相位误差。鉴于非线性相位误差的频率是理想相位的3倍，通过使用SHE方法进一步减少非线性相位误差。然后通过Hermite插值算法拟合连续函数，可以减少SHE方法引入的离散化误差。通过对单物体与不连续复杂物体进行实验，结果表明，本文所提出的鲁棒相位编码方法具有有效性与鲁棒性。

1 原理

1.1 相移与相位编码法

三步相移法只需要3幅条纹图案，gamma非线性对其影响明显。在不失一般性的情况下，本文选择了三步相移方法作为例子。图1展示了传统相移加相位编码方法的原理。

图 1 传统相移加相位编码方法的原理图

Figure 1. Schematic diagram of traditional phase-shifting plus phase-coding method

下载: 全尺寸图片幻灯片

获得具有相等相移量的条纹图案可以表示为

$$ {I_n}(x,y) = a(x,y) + b(x,y)\cos (\phi + {\delta _n}) $$

(1)

式中：$ n=1,2,3 $；$ (x, y) $表示像素坐标；$ a(x, y) $与$ b(x, y) $分别表示条纹图背景光强和调度强度；$ \delta_{n}=-2 \pi / 3, 0,+2 \pi / 3 $是3幅条纹图案的相移量；$ \phi(x, y) $是相位，可通过如下公式进行求解：

$$ \phi (x,y) = {\tan ^{ - 1}}\left[ {\sqrt 3 ({I_1} - {I_3})/(2{I_2} - {I_1} - {I_3})} \right] $$

(2)

反正切函数将相位截断在0～2π定义域范围内，具有2π不连续性。为了恢复连续分布的绝对相位，采用相位编码的方法来消除2π不连续性。通常，相位编码方法需要两组条纹图案：3幅正弦条纹图案和3幅相位编码条纹图案，分别用于提取包裹相位和确定条纹级次的阶梯相位。其中，3幅正弦条纹图案可通过式（2）获得包裹相位，确定的条纹级次用来准确展开包裹相位。对于条纹级次的确定，首先将码字嵌入到阶梯相位中，如下所示。

$$ {\phi ^{\mathrm{s}}}(x,y) = {\mathrm{floor}}(x/T) \times 2\pi /K $$

(3)

式中：$ {\mathrm{floor}}(x/T) $表示每个像素的条纹级次的截断整数；$ T $是每个条纹周期的像素数；$ K $是条纹周期的总数；$ {\phi ^{\mathrm{s}}}(x,y) $是阶梯相位。其次，我们将阶梯相位编码为3幅相位编码条纹图案，可以描述为

$$ I_n^{\mathrm{s}}(x,y) = a(x,y) + b(x,y)\cos ({\phi ^{\mathrm{s}}} + {\delta _n}) $$

(4)

通过三步相移算法可从相应捕获的条纹图案中恢复阶梯相位。因为阶梯相位被编码范围为0～2π，不需要相位展开，阶梯相位变化与包裹相位的2π不连续性一致。因此，从阶梯相位中确定的条纹级次$ k(x,y) $可以描述为

$$ k(x,y) = {\mathrm{round}}(K{\phi ^{\mathrm{s}}}/2\pi ) $$

(5)

式中$ {\mathrm{round}}(·) $代表四舍五入取最接近的整数。确定了条纹级次，通过式（6）就可以将包裹相位展开为绝对相位$ \varPhi (x,y) $。

$$ \varPhi (x,y) = \phi (x,y) + 2\pi k(x,y) $$

(6)

1.2 Gamma非线性引入的周期性相位误差

条纹投影技术中通常采用商用投影仪和相机，它们被制造为非线性器件。式（7）描述了非线性器件对第i个理想条纹图案输入强度的真实响应。由于大于五阶谐波的振幅通常很小，因此可以忽略，傅里叶级数展开成：

$$ \begin{split} I_i^{\mathrm{c}}(x,y) =& f\left[ {{I_i}(x,y)} \right] \approx\\ & a(x,y) + \sum\nolimits_{j = 1}^5 {{b_j}(x,y)\left\{ {j[\phi (x,y) + {\delta _i}]} \right\}} \\ \end{split} $$

(7)

式中：$ I_i^{\mathrm{c}}(x,y) $是实际投影条纹图案的强度；$ f[·] $代表gamma非线性函数；$ {b_j} $是条纹图案的调制度。在本文中，除非另有说明，相位均为包裹相位。使用相移算法计算的测量相位$ \phi '(x,y) $可以写成：

$$ \phi '(x,y) = - \arctan \left\{ {\frac{{\displaystyle\sum\nolimits_{i = 0}^{N - 1} {\left\{ {a(x,y) + \displaystyle\sum\nolimits_{j = 1}^5 {{b_j}(x,y)\left\{ {j[\phi (x,y) + {\delta _i}]} \right\}} } \right\}{\text{sin}}({\delta _i})} }}{{\displaystyle\sum\nolimits_{i = 0}^{N - 1} {\left\{ {a(x,y) + \displaystyle\sum\nolimits_{j = 1}^5 {{b_j}(x,y)\left\{ {j[\phi (x,y) + {\delta _i}]} \right\}} } \right\}{\text{cos}}({\delta _i})} }}} \right\} $$

(8)

当N = 3时，式（8）可被进一步推导为

$$ \phi '(x,y) = \arctan \left\{ {\frac{{{b_1}\sin \left[ {\phi (x,y)} \right] - {b_2}\sin \left[ {2\phi (x,y)} \right] + {b_4}\sin [4\phi (x,y)] - {b_5}\sin \left[ {5\phi (x,y)} \right]}}{{{b_1}\cos \left[ {\phi (x,y)} \right] + {b_2}\cos \left[ {2\phi (x,y)} \right] + {b_4}\cos [4\phi (x,y)] + {b_5}\cos \left[ {5\phi (x,y)} \right]}}} \right\} $$

(9)

系统的gamma非线性不可避免地会导致捕获的条纹图案偏离理想分布，并引入附加的相位误差$\Delta \phi (x,y)$。测量的相位$ \phi '(x,y) $可以认为是理想相位$ \phi (x,y) $和gamma非线性引入附加相位误差$\Delta \phi (x,y)$的总和。

$$ \phi '(x,y) = \phi (x,y) + \Delta \phi (x,y) $$

(10)

因此，附加的相位误差可以近似为

$$ \begin{split} &\Delta \phi (x,y) = \phi '(x,y) - \phi (x,y) \approx \\ & - \arctan \left[ {\frac{{({a_2} - {a_4})\sin (3\phi ) + {a_5}\sin (6\phi )}}{{{a_1} + ({a_2} + {a_4})\cos (3\phi ) + {a_5}\cos (6\phi )}}} \right] \approx \;\;\;\; \\ &- {c_1}\sin (3\phi ) - {c_2}\sin (6\phi ) \\ \end{split} $$

(11)

式中${c_1}$和${c_2}$是系数。由上式可以看出，当存在任何gamma非线性时，附加的相位误差$\Delta \phi (x,y)$是周期性的，可以看作是理想相位$ \phi (x,y) $的函数。

1.3 Gamma非线性相位误差的概率分布

投影仪的像素位置在水平或垂直方向上单调增加。由于连续的相位分布，相位值的概率是相等的，使用式（12）来描述包裹相位的概率。

$$ F(k) = P\{ 2\pi (k - 1)/K < \phi < 2\pi k/K\} $$

(12)

式中： $ P\{·\} $表示概率；$k{\text{ = }}1,2, \cdots ,K$；$K$表示从0到2π的步长，可以是任意整数。当相位值被包裹在0～2π内时，由于周期性，包裹相位值的概率是相等的，因此概率分布函数曲线是均匀的。当系统中出现任何gamma非线性时，通过推导式（10）和式（11），相位变化可以写成式（13）：

$$ \begin{split} \frac{{\partial \phi '(x,y)}}{{\partial x}} = &\frac{{\partial \phi (x,y)}}{{\partial x}}\left\{ {1 - 3{c_1}\cos\left[ {3\phi (x,y)} \right] -} \right.\\ &\left. { 6{c_2}\cos\left[ {6\phi (x,y)} \right]} \right\} \end{split} $$

(13)

根据式（13）可以看出测量相位的变化不再均匀，这将导致测量的相位值的概率不等于理想相位值的概率^[27]，进而使得概率分布函数曲线变得不均匀。已有研究对正弦结构光中的相位和强度进行数值概率分析，结果表明相位的概率调整比强度的概率调整对于相位线性化更为有效^[25]。鉴于理想相位值的概率相等，且附加相位误差可视为理想相位的函数，则可对测量相位值的概率进行调整来校正非线性相位误差。

1.4 鲁棒相位编码方法的原理

在上述值概率分析方法的基础上，本文提出了一种鲁棒的相位编码方法，该方法可校正由系统的gamma非线性引起的相位误差。图2显示了校正过程。

在鲁棒相位编码方法中，使用直方图累积分布函数作为变换公式。

$$ {S_k} = \sum\nolimits_{i = 0}^k {{P_r}({r_i})} = \sum\nolimits_{i = 0}^k {{n_i}/N} $$

(14)

式中：${r_i}$为输入相位值；${S_k}$为输入相位累计分布频率；$N$是图案中像素的总和；${n_i}$是当前相位值的像素数。需要注意的是$0 \leqslant {S_k} \leqslant 1$。通过式（15）可以得到一个整数。

$$ R(k) = {\mathrm{round}}[K \times {S_k}] $$

(15)

式中$ {\mathrm{round}}[·] $代表四舍五入取最接近的整数，因此，可以很容易确定$R(k)$的范围为$0 \leqslant R(k) \leqslant K$。相应均衡后的相位应映射为

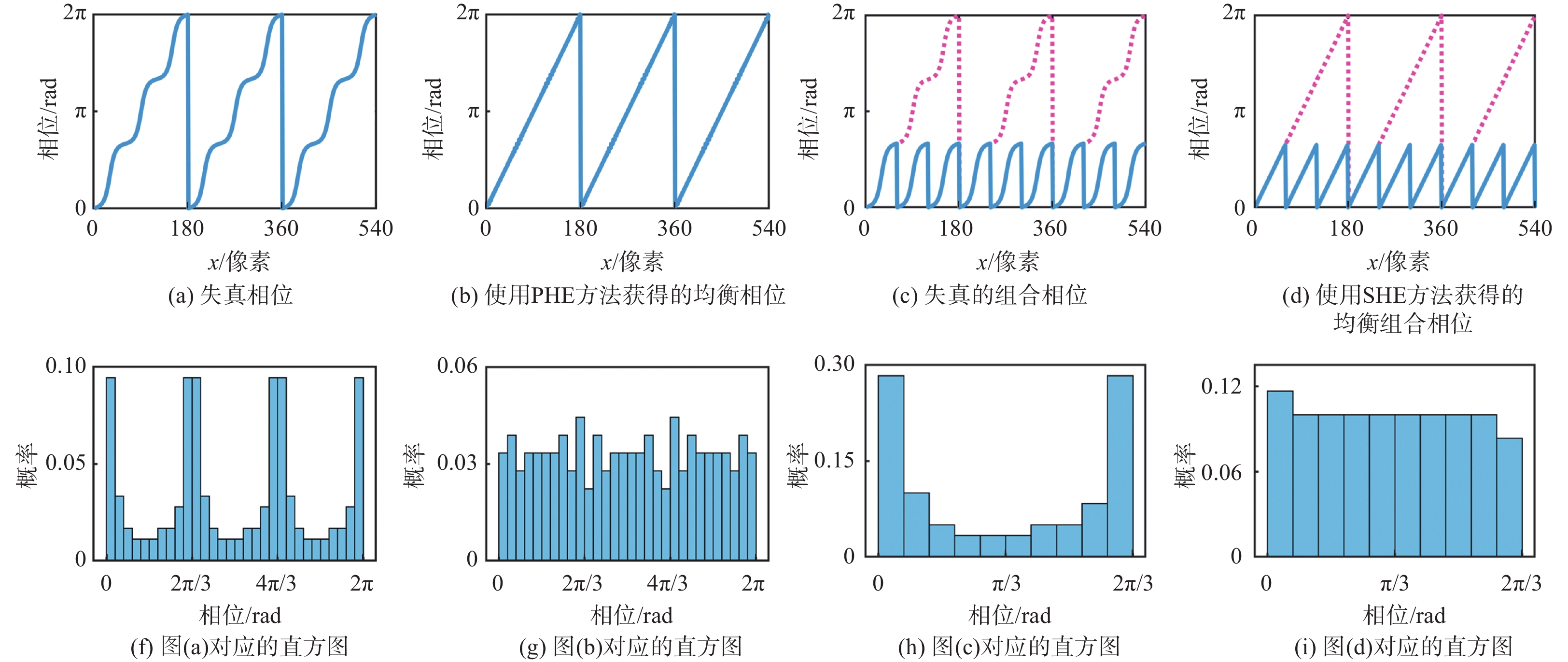
$$ \phi = R(k) \times 2\pi /K $$

(16)

图 2 算法流程图

Figure 2. Flow chart of algorithm

下载: 全尺寸图片幻灯片

图3为鲁棒相位编码方法原理图。图3(a)绘制了失真相位截面曲线，在每个条纹周期内（每周期180像素），失真相位不会随着横坐标线性增加。图3(f)显示了一个周期内的直方图，可以明显看出不同相位值的概率彼此不相等。如图3(b)所示，通过实施PHE方法，周期性相位误差明显减少，与图3(f)所示的直方图相比，相位值的概率分布相对均匀。如图3(f)所示，失真相位的直方图是周期性的，包含3个近似的谷。式（11）已推导出非线性相位误差的频率是理想相位的频率的3倍。从图3(f)中可以看出，相位域中非线性相位误差的周期为2π/3，是理想相位的1/3，[0, 2π/3]、[2π/3, 4π/3]和[4π/3, 2π]这3个区间内失真相位的直方图是近似相同的。因此，可以将上述3个间隔的相位进行组合，组合后的相位将与原始相位共享相同的直方图，采样像素的数量将增加3倍。为了进一步减少误差，本文提出SHE方法来调整组合后的相位概率分布，使用式（17）对其进行详细描述：

$$ \alpha {\text{ = }}\text{mod} \left( {\phi ,{{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. } 3}} \right) $$

(17)

式中：$ \mathrm{mod}(·) $代表返回两个输入量的余数；$\alpha $代表1/3周期相位。另外，用于标识第1个1/3周期、第2个1/3周期和第3个1/3周期的整数$ \beta $可以计算为

$$ \beta = {\mathrm{floor}}{\text{[3}}\phi {\text{/(}}2\pi {\text{)]}} $$

(18)

式中$ {\mathrm{floor}}[·] $返回小于或等于输入值的最近整数。类似地，对组合相位再次应用上述直方图均衡。图3(h)和图3(i)分别显示了使用SHE方法前后的组合相位直方图。均衡后的组合相位可以通过式（19）恢复：

$$ \phi = \alpha + 2\pi \beta /3 $$

(19)

SHE方法将连续相位均衡化为离散相位，这将引入一些离散化误差。为了进一步减小离散化误差，本文采用了Hermite插值算法来拟合连续函数。插值方法是数值分析中一种简单而重要的方法，该方法可通过函数在有限点处的函数值求出其近似函数，进而计算出函数在其他点处的值^[28]。因此，Hermite插值算法的应用有助于减少SHE方法引入的离散化误差。

$$ S\left( \phi \right) = {\mathrm{Hermite}}\left( {X,Y} \right) $$

(20)

式中：$ {\mathrm{Hermite}}(·) $表示Hermite插值函数；$ Y = \left[ {{y_1},{y_2}, \cdots,{y_k}} \right] $，$ {y_k} $表示均衡后的离散相位值；$ X = \left[ {{x_1},{x_2}, \cdots ,{x_k}} \right] $，$ {x_k} $是对应于均衡相位的每个离散值$ {y_k} $的失真相位的平均值；$ ({x_k},{y_k}) $是插值节点。然后，通过对由$ {x_k} $和$ {y_k} $组成的点进行Hermite插值来建立连续函数。利用连续函数对包裹相位和阶梯相位进行校正，消除直方图均衡化的离散化误差。根据上述方法，可以获得校正的包裹相位和阶梯相位，进而得到修正后的条纹阶次。通过式（6）对包裹相位进行相位展开。最后，消除了由系统的gamma非线性引起的相位误差。

图 3 鲁棒相位编码方法原理。

Figure 3. Schematic diagram of robust phase-coding method

下载: 全尺寸图片幻灯片

2 仿真实验设计

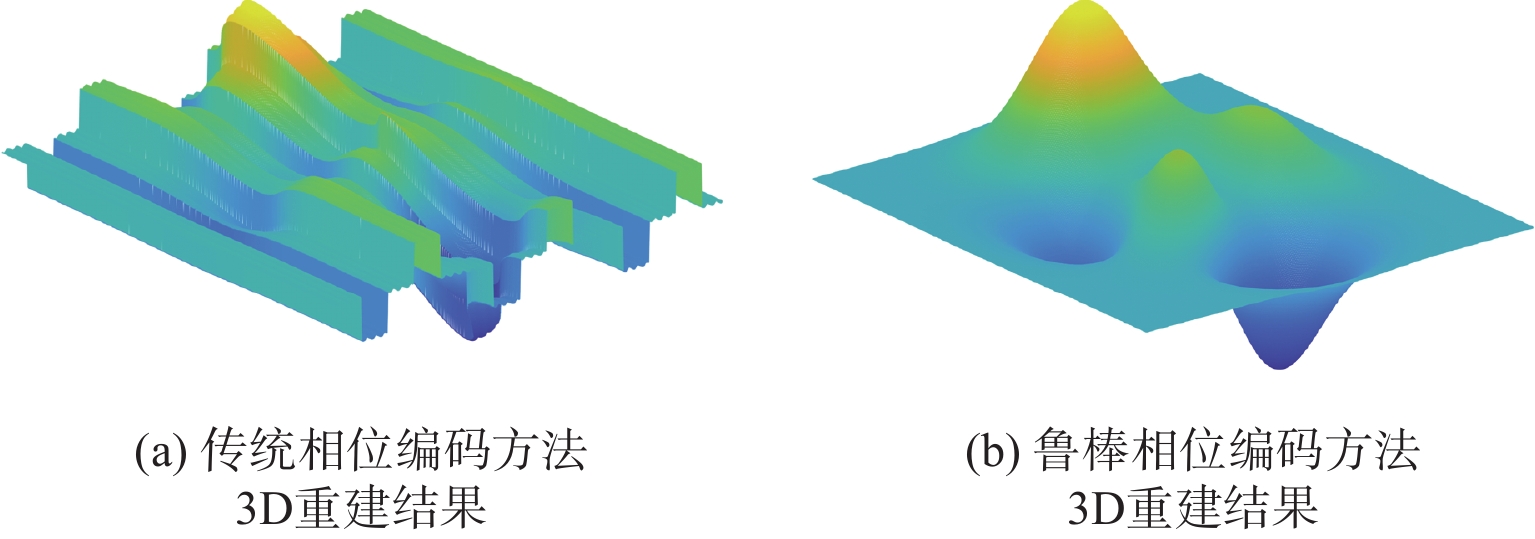
为了评估所提方法的有效性，本实验使用peaks峰值函数来模拟被测物体表面。其中，正弦条纹的周期被设置为30个像素，生成分辨率为450×450像素的模拟条纹图案，gamma值设置为$\gamma {\text{ = 2}}$。使用本文提出的鲁棒相位编码方法对模拟条纹图案进行处理。图4(a)和4(b)分别显示了使用传统相位编码方法和鲁棒相位编码方法获得的3D重建结果。如图4(a)所示，由于gamma非线性的影响，传统方法3D重建结果不令人满意。如图4(b)所示，利用鲁棒相位编码方法3D重建结果表面平滑，证明了鲁棒相位编码方法的有效性。

图 4 重建的对象

Figure 4. Reconstructed object

下载: 全尺寸图片幻灯片

图5绘制了包裹相位、阶梯相位和条纹级次的横截面。如图5(a)所示，条纹级次与传统相位编码方法获得的包裹相位和阶梯相位显示出很大的不一致性。由于gamma非线性的影响，当相邻量化相位之间的差较小时，条纹级次不能正确求解。例如，相同的条纹级次对应于非唯一的包裹相位和阶梯相位，这可能导致相位展开产生严重错误。比较图5(a)和图5(b)可以发现，校正后的每个条纹级次对应唯一的包裹相位和阶梯相位，同时，使用本文提出的鲁棒相位编码方法后，包裹相位是线性的，很好地校正了由gamma非线性引起的相位误差。

图 5 包裹相位、阶梯相位和条纹级次的横截面

Figure 5. Cross section of wrapped phase, stair phase and fringe order

下载: 全尺寸图片幻灯片

本文设计了比较实验来评估提出的鲁棒相位编码方法的准确性，实验结果如图6所示。gamma值设置为$\gamma {\text{ = 2}}$。利用传统的相位编码方法获得物体失真的绝对相位，并通过减去理想的绝对相位图来计算相位误差图。图6(a)显示了理想的绝对相位图。图6(b)显示了通过传统方法获得的相位误差图。图6(c)和6(d)分别显示了PHE校正后和进一步插值后的相位误差图。图6(e)和6(f)分别显示了SHE校正后和进一步插值后的相位误差图。可以清楚地看出，相位误差在显著减小。为了量化相位误差，还计算了相位误差的均方根（root mean square, RMS）。图6(b)～6(f)中相位误差的RMS分别为0.1782 rad、0.0267 rad、0.0190 rad、0.0104 rad和0.0077 rad。与传统的相位编码方法相比，鲁棒相位编码方法相位误差的RMS降低了0.1705 rad。因此，鲁棒相位编码方法可以有效地降低gamma非线性引起的周期性相位误差。

为了评估所提方法的鲁棒性，实验模拟了不同gamma值下相位误差的RMS。gamma值以0.1为步长在1.5到3.5之间变化。图7绘制了不同gamma值下相位误差的RMS曲线。从图7可以看出，通过SHE校正及进一步Hermite插值方法校正的相位误差的RMS曲线随着gamma值的增加而稳定。这表明SHE校正和进一步的Hermite插值方法对不同的伽玛值是鲁棒的。从图6和图7可以看出，本文所提方法具有鲁棒性。

图 6 实验结果

Figure 6. Experimental results

下载: 全尺寸图片幻灯片

图 7 不同gamma值下相位误差的RMS曲线。

Figure 7. RMS curves of phase errors under different gamma values

下载: 全尺寸图片幻灯片

3 实验结果与分析

本实验搭建了条纹投影系统来测试所提出的鲁棒相位编码方法。该系统包括一个DLP投影仪和一个CMOS相机。相机分辨率为1280×1024像素，投影仪分辨率为912×1140像素。正弦条纹和相位编码条纹被设置为每周期42像素。3幅相位编码条纹图案和3幅正弦条纹图案依次投影到物体上，同时相机捕获相应的反射图像。首先测量了一个蝴蝶雕塑，如图8所示。图8(a)和8(b)分别显示了使用传统相位编码方法和鲁棒相位编码方法获得的3D重建结果。图8(a)所示结果存在一些严重的相位误差，由于gamma非线性的影响导致部分条纹级次产生错误，进一步导致相位展开错误，例如图8(a)中的红色和蓝色区域。如图8(b)所示，使用鲁棒相位编码方法之后的物体表面是平坦的，通过对结果进行比较和分析，可以看出鲁棒相位编码方法有效的校正了gamma非线性相位误差。

图 8 重建的雕塑

Figure 8. Reconstructed sculpture

下载: 全尺寸图片幻灯片

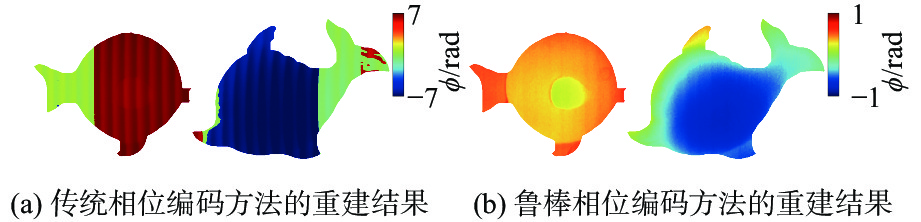
相位误差如图9所示。鉴于大步相移方法可以获得高精度的绝对相位图，本文使用大步相移法获得的相位图作为理想的绝对相位图，如图9(a)所示。同理，其余方法得到的绝对相位图与理想的绝对相位图相减来计算相位误差图。图9(b)显示了通过传统方法获得的相位误差图。图9(c)和图9(d)分别显示了PHE校正后和进一步插值方法后的相位误差图。图9(b)～图9(d)中相位误差的RMS值分别为3.7140 rad、0.0539 rad和0.0529 rad。可以清楚地看到，相位误差显著减小。为了进一步提高精度，进行了SHE校正和进一步的插值方法，图9(e)和图9(f)分别显示了校正后的相位误差图，其RMS值分别为0.0097 rad和0.0091 rad。比较图9(b)和图9(f)，可以发现由gamma非线性引起的相位误差也得到了很好的校正。结果验证了提出的鲁棒相位编码方法的有效性。

图 9 相位误差图

Figure 9. Phase error diagram

下载: 全尺寸图片幻灯片

为了进一步验证鲁棒相位编码方法对不连续复杂物体的校正效果，同时测量了两个具有复杂表面的石膏雕塑,如图10、图11所示。图10(a)和图10(b)展示了使用传统相位编码方法和鲁棒相位编码方法获取的重建结果。由于条纹投影系统中的gamma非线性效应，部分条纹级次求解产生了错误，进而导致部分相位展开错误，如图10(a)中的红色和蓝色区域所示。与图11(a)中通过大步相移得到的理想绝对相位图相比，图10(a)中存在明显的周期性相位误差。相反地，图10(b)中的周期性相位误差明显减小，同时解决了条纹级次求解错误的问题，正确展开了包裹相位。类似地，为了量化相位误差，还计算了相位误差图的RMS。在传统的相位编码方法中，由于错误条纹级次的影响，图11(b)所示的相位误差相对较大。使用上述方法校正后，图11(b)～图11(f)所示相位误差图的RMS值分别为5.5528 rad、0.0352 rad、0.0337 rad、0.0106 rad和0.0101 rad。通过比较图11(b)和图11(f)，可以看出鲁棒相位编码方法可以求解出正确的条纹阶数，同时显著消除周期性相位误差。实验结果表明，鲁棒相位编码方法可以有效地解决由gamma非线性引起的相位误差问题。

图 10 重建不连续雕塑

Figure 10. Reconstructed discontinuous sculpture

下载: 全尺寸图片幻灯片

图 11 相位误差图

Figure 11. Phase error diagram

下载: 全尺寸图片幻灯片

4 结论

针对gamma非线性对传统相位编码方法的影响，提出了一种鲁棒相位编码方法。在该方法中，使用SHE方法来调整失真相位，并获得离散分布的校正相位。但是，这种方法得到的相位会有一定的离散化误差。为了避免该问题，采用Hermite插值算法拟合连续函数来减小离散误差。该方法解决了由gamma非线性引起的周期性相位误差问题。仿真实验和多组真实实验结果表明了鲁棒相位编码方法的可行性和有效性。该方法提高了传统相位编码方法的鲁棒性，具有广阔的应用前景。

图 1 传统相移加相位编码方法的原理图

Figure 1. Schematic diagram of traditional phase-shifting plus phase-coding method

下载: 全尺寸图片幻灯片

图 2 算法流程图

Figure 2. Flow chart of algorithm

下载: 全尺寸图片幻灯片

图 3 鲁棒相位编码方法原理。

Figure 3. Schematic diagram of robust phase-coding method

下载: 全尺寸图片幻灯片

图 4 重建的对象

Figure 4. Reconstructed object

下载: 全尺寸图片幻灯片

图 5 包裹相位、阶梯相位和条纹级次的横截面

Figure 5. Cross section of wrapped phase, stair phase and fringe order

下载: 全尺寸图片幻灯片

图 6 实验结果

Figure 6. Experimental results

下载: 全尺寸图片幻灯片

图 7 不同gamma值下相位误差的RMS曲线。

Figure 7. RMS curves of phase errors under different gamma values

下载: 全尺寸图片幻灯片

图 8 重建的雕塑

Figure 8. Reconstructed sculpture

下载: 全尺寸图片幻灯片

图 9 相位误差图

Figure 9. Phase error diagram

下载: 全尺寸图片幻灯片

图 10 重建不连续雕塑

Figure 10. Reconstructed discontinuous sculpture

下载: 全尺寸图片幻灯片

图 11 相位误差图

Figure 11. Phase error diagram

下载: 全尺寸图片幻灯片

参考文献(28)

[1]	左超, 张晓磊, 胡岩, 等. 3D 真的来了吗?——三维结构光传感器漫谈[J]. 红外与激光工程, 2020, 49(3): 0303001-0303001-45. doi: 10.3788/IRLA202049.0303001 ZUO Chao, ZHANG Xiaolei, HU Yan, et al. Has 3D finally come of age? an introduction to 3D structured-light sensor[J]. Infrared and Laser Engineering, 2020, 49(3): 0303001-0303001-45. doi: 10.3788/IRLA202049.0303001
[2]	GORTHI S S, RASTOGI P. Fringe projection techniques: whither we are?[J]. Optics and Lasers in Engineering, 2010, 48: 133-140. doi: 10.1016/j.optlaseng.2009.09.001
[3]	殷永凯, 张宗华, 刘晓利, 等. 条纹投影轮廓术系统模型与标定综述[J]. 红外与激光工程, 2020, 49(3): 0303008-0303008-18. doi: 10.3788/IRLA202049.0303008 YIN Yongkai, ZHANG Zonghua, LIU Xiaoli, et al. Review of the system model and calibration for fringe projection profilometry[J]. Infrared and Laser Engineering, 2020, 49(3): 0303008-0303008-18. doi: 10.3788/IRLA202049.0303008
[4]	YU X, LIU Y, CHEN W. Efficient phase-shift error compensation algorithm based on probability density function[J]. Optics and Lasers in Engineering, 2022, 153: 107007.
[5]	苏显渝, 张启灿, 陈文静. 结构光三维成像技术[J]. 中国激光, 2014, 41(2): 0209001. doi: 10.3788/CJL201441.0209001 SU Xianyu, ZHANG Qican, CHEN Wenjing. Three-dimensional imaging based on structured illumination[J]. Chinese Journal of Lasers, 2014, 41(2): 0209001. doi: 10.3788/CJL201441.0209001
[6]	WANG Y, ZHU H, WANG Y, et al. Efficient half-period phase histogram equalization for general phase-shifting algorithms with phase shift errors[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1-10.
[7]	ZHANG S. High-speed 3D shape measurement with structured light methods: a review[J]. Optics and Lasers in Engineering, 2018, 106: 119-31.
[8]	ZUO C, FENG S, HUANG L, et al. Phase shifting algorithms for fringe projection profilometry: a review[J]. Optics and Lasers in Engineering, 2018, 109: 23-59. doi: 10.1016/j.optlaseng.2018.04.019
[9]	ZHANG R, DUAN M, FAN X, et al. Deep learning-enabled anti-ambient light approach for fringe projection profilometry[J]. Optics Express, 2022, 30(26): 47672-47689. doi: 10.1364/OE.477747
[10]	YAO P, GAI S, DA F. Super-resolution technique for dense 3D reconstruction in fringe projection profilometry[J]. Optics Letters, 2021, 46(18): 4442-4445. doi: 10.1364/OL.431676
[11]	LI J, DING S, ZENG Z, et al. Dual-biprism-based coaxial fringe projection system[J]. Applied Optics, 2022, 61(14): 3957-3964. doi: 10.1364/AO.458716
[12]	WANG Y, XU H, ZHU H, et al. Pixel-wise phase unwrapping with adaptive reference phase estimation for 3D shape measurement[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 1-9.
[13]	WU Z B, TAO W, LYV N, et al. Self-correction of fringe order jump error induced by system nonlinearity based on phase-coding method[J]. Optical Review, 2023, 4: 436-453.
[14]	史耀群, 邓林嘉, 王朝旭, 等. 一种基于结构光条纹投影的微小物体测量系统[J]. 应用光学, 2019, 40(6): 1120-1125. doi: 10.5768/JAO201940.0603007 SHI Yaoqun, DENG Linjia, WANG Zhaoxu, et al. Micro-objects measurement system based on structured light fringe projection[J]. Journal of Applied Optics, 2019, 40(6): 1120-1125. doi: 10.5768/JAO201940.0603007
[15]	ZHANG S. Absolute phase retrieval methods for digital fringe projection profilometry: a review[J]. Optics and Lasers in Engineering, 2018, 107: 28-37. doi: 10.1016/j.optlaseng.2018.03.003
[16]	张启灿, 吴周杰. 基于格雷码图案投影的结构光三维成像技术[J]. 红外与激光工程, 2020, 49(3): 0303004-0303004-13. doi: 10.3788/IRLA202049.0303004 ZHANG Qican, WU Zhoujie. Three-dimensional imaging technique based on Gray-coded structured illumination[J]. Infrared and Laser Engineering, 2020, 49(3): 0303004-0303004-13. doi: 10.3788/IRLA202049.0303004
[17]	WANG Y, ZHANG S. Novel phase-coding method for absolute phase retrieval[J]. Optics Letters, 2012, 37(11): 2067-2069. doi: 10.1364/OL.37.002067
[18]	WANG Y, XU H, ZHU H, et al. Pixel-wise phase unwrapping with adaptive reference phase estimation for 3-D shape measurement[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 1-9.
[19]	ZHENG Y, JIN Y, DUAN M, et al. Joint coding strategy of the phase domain and intensity domain for absolute phase retrieval[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-8.
[20]	ZHENG D, DA F. Phase coding method for absolute phase retrieval with a large number of codewords[J]. Optics Express, 2012, 20(22): 24139-24150. doi: 10.1364/OE.20.024139
[21]	WANG Y, CHEN X, HUANG L, et al. Improved phase-coding methods with fewer patterns for 3D shape measurement[J]. Optics Communications, 2017, 401: 6-10. doi: 10.1016/j.optcom.2017.05.024
[22]	WANG L, CHEN Y, HAN X, et al. A 3D shape measurement method based on novel segmented quantization phase coding[J]. Optics and Lasers in Engineering, 2019, 113: 62-70. doi: 10.1016/j.optlaseng.2018.10.004
[23]	LIU K, WANG S, LAU D L, et al. Nonlinearity calibrating algorithm for structured light illumination[J]. Optical Engineering, 2014, 53(5): 050501. doi: 10.1117/1.OE.53.5.050501
[24]	CHEN H, YIN Y, CAI Z, et al. Suppression of the nonlinear phase error in phase shifting profilometry: considering non-smooth reflectivity and fractional period[J]. Optics Express, 2018, 26(10): 13489-13505. doi: 10.1364/OE.26.013489
[25]	JE C, PARK H-M. Value probability analysis for linear phase estimation in sinusoidal structured-light range imaging[J]. Optics Letters, 2021, 46(3): 476-479. doi: 10.1364/OL.416828
[26]	XING Y, QUAN C, TAY C J. A modified phase-coding method for absolute phase retrieval[J]. Optics and Lasers in Engineering, 2016, 87: 97-102. doi: 10.1016/j.optlaseng.2016.03.018
[27]	LIU Y, YU X, XUE J, et al. A flexible phase error compensation method based on probability distribution functions in phase measuring profilometry[J]. Optics & Laser Technology, 2020, 129: 106267.
[28]	RABBATH C, CORRIVEAU D. A comparison of piecewise cubic Hermite interpolating polynomials, cubic splines and piecewise linear functions for the approximation of projectile aerodynamics[J]. Defence Technology, 2019, 15(5): 741-757. doi: 10.1016/j.dt.2019.07.016

施引文献

资源附件(0)

图(11)

计量

文章访问数: 73
HTML全文浏览量: 22
PDF下载量: 30
被引次数: 0

引言
1 原理
1.1 相移与相位编码法
1.2 Gamma非线性引入的周期性相位误差
1.3 Gamma非线性相位误差的概率分布
1.4 鲁棒相位编码方法的原理
2 仿真实验设计
3 实验结果与分析
4 结论

用于绝对相位恢复的鲁棒相位编码方法

作者简介:
朱浩杰（1996—），男，硕士研究生，主要从事光学三维测量研究。E-mail：zhjand@stu.ahau.edu.cn

通讯作者:
侯文慧（1985—），女，博士，讲师，主要从事智慧农业研究。E-mail：hwh303@ahau.edu.cn

计量

Robust phase-coding method for absolute phase retrieval

引言