基于角度交会的二维坐标图像测量系统

程瑶, 许文斌, 刘云阳

程瑶, 许文斌, 刘云阳. 基于角度交会的二维坐标图像测量系统[J]. 应用光学, 2024, 45(2): 438-445. DOI: 10.5768/JAO202445.0203006
引用本文: 程瑶, 许文斌, 刘云阳. 基于角度交会的二维坐标图像测量系统[J]. 应用光学, 2024, 45(2): 438-445. DOI: 10.5768/JAO202445.0203006
shu
CHENG Yao, XU Wenbin, LIU Yunyang. Two-dimensional coordinate image measurement system based on angle intersection[J]. Journal of Applied Optics, 2024, 45(2): 438-445. DOI: 10.5768/JAO202445.0203006
Citation: CHENG Yao, XU Wenbin, LIU Yunyang. Two-dimensional coordinate image measurement system based on angle intersection[J]. Journal of Applied Optics, 2024, 45(2): 438-445. DOI: 10.5768/JAO202445.0203006
shu

基于角度交会的二维坐标图像测量系统

  • 重庆理工大学 机械工程学院，重庆 400050

基金项目: 国家自然科学基金（52375526）；重庆市研究生科研创新项目（CYS22653）；重庆市科委基础与前沿研究一般项目（cstc2016jcyjA0497）；重庆市教委科学技术研究项目（KJQN202301108）；重庆理工大学研究生教育高质量发展项目（gzlcx20232126）
详细信息
    作者简介:

    程瑶（1981—），女，硕士，副教授，主要从事图像检测及处理等研究。E-mail：chy_cqit@cqut.edu.cn

    通讯作者:

    许文斌（1996—），男，硕士，主要从事图像处理和并联机构等研究。E-mail：1602361393@qq.com

  • 中图分类号: TN29

Two-dimensional coordinate image measurement system based on angle intersection

  • College of Mechanical Engineering, Chongqing University of Technology, Chongqing 400050, China

HTML全文

    摘要
  • 摘要:

    针对基准平面障碍物检测定位问题，设计了一种采用角度交会法测量二维坐标的嵌入式图像检测系统。二维坐标测量系统采用双线法标定线阵CCD图像传感器，并采用角度交会法对被测对象进行坐标计算，从而测得未修正的二维坐标测量结果。采用控制变量法分别测量X轴和Y轴坐标，使用Matlab软件对数据进行处理，并对X轴和Y轴测量误差分别进行多项式线性拟合，进而得到坐标修正公式，修正的二维坐标误差明显变小。实验结果表明：基于角度交会的二维坐标图像测量系统能够实时、准确、快速和可靠地测量二维坐标，为基准平面障碍物二维坐标测量定位提供了一种可行的方案，具有一定的应用价值和意义。

    Abstract:

    Aiming at the problem of detection and positioning of reference plane obstacles, an embedded image detection system using angle intersection method to measure two-dimensional coordinates was designed. The two-line method was adopted to calibrate the linear array CCD image sensor by two-dimensional coordinate measurement system, and the angle intersection method was used to calculate the coordinates of the measured object, so that the uncorrected two-dimensional coordinate measurement results were obtained. The control variable method was used to measure the coordinates of X axis and Y axis, respectively, the Matlab software was used to process the data, and the polynomial linear fitting of the measurement errors of X axis and Y axis was carried out respectively to obtain the coordinate correction formula, in which the corrected two-dimensional coordinate errors became significantly smaller. The experimental results show that the two-dimensional coordinate image measurement system based on angle intersection can measure two-dimensional coordinates in real time, accurately, quickly and reliably, and provides a feasible scheme for two-dimensional coordinate measurement of reference plane obstacles, which has certain application values and significance.

    • HTML全文

  • 引言

    线阵CCD图像传感器具有视野极大、扫描频率高、分辨率高等特点，广泛应用于非接触式测量和表面检测等领域[1]。二维坐标测量系统主要是对基准面上的坐标进行测量，广泛应用于机床、路径规划、障碍定位等领域[2]。目前，坐标测量可以分为接触式测量和非接触式测量，接触式测量具有适用范围的局限性，而非接触式测量具有广泛的适用范围，非接触式测量方法主要有激光扫描、影像测量、照相测量和工业CT扫描等[3]。激光扫描方法由半导体激光器发出激光，聚光透镜在被测曲面上结成光电并反射，利用光敏元件接收其散射光，根据其在光敏元件上的位置，从而测出被测点的坐标位置[4]。如朱博源等[5]将多个角锥棱镜作为无源待测靶点，通过构建非球面反射接收模型实现了信号发射端与接收端的结合，建立了多靶点光信号匹配机制以实现无源多靶点交会定位；影像测量方法通过光学放大系统对被测物体放大，CCD图像采集系统采集图像特征并送入计算机，实现高效地检测[6]。如白玮本等[7]采用基于结构光的嵌入式图像采集系统，借助光栅发生器对被测物进行扫描，CCD相机抓取被测物光条纹信息，通过以太网传输至PC端；照相测量方法通过相机多角度采集被测对象得到图像信息，依据空间物体投影原理，利用被测对象表面的标志点特征计算被测对象的三维空间信息，多应用于三维重构领域[8]；工业CT扫描方法是将计算机断层成像技术应用于工业中，其基本原理是依据辐射在被检测物体中的减弱和吸收特性，广泛应用于医学和三维重构领域[9-10]；角度交会法通过两个角度的测量进而计算得到被测对象坐标，具有测量精度高，适用范围广等特点，广泛应用于工程项目[11]。

    综上所述，基于影像测量法的高效优势和角度交会法的高精度特点，针对基准平面障碍物检测定位问题，本文设计了一种基于角度交会的嵌入式二维坐标图像测量系统，将图像检测技术应用于二维坐标测量，可以发挥线阵CCD图像传感器大视野、高扫描频率、高分辨率和嵌入式设备实时性高等优势，能够实时、准确、快速和高效地测量显示障碍物二维坐标，可以广泛应用于基准平面障碍物检测定位，具有一定的实用价值和意义。

    1   系统测量原理

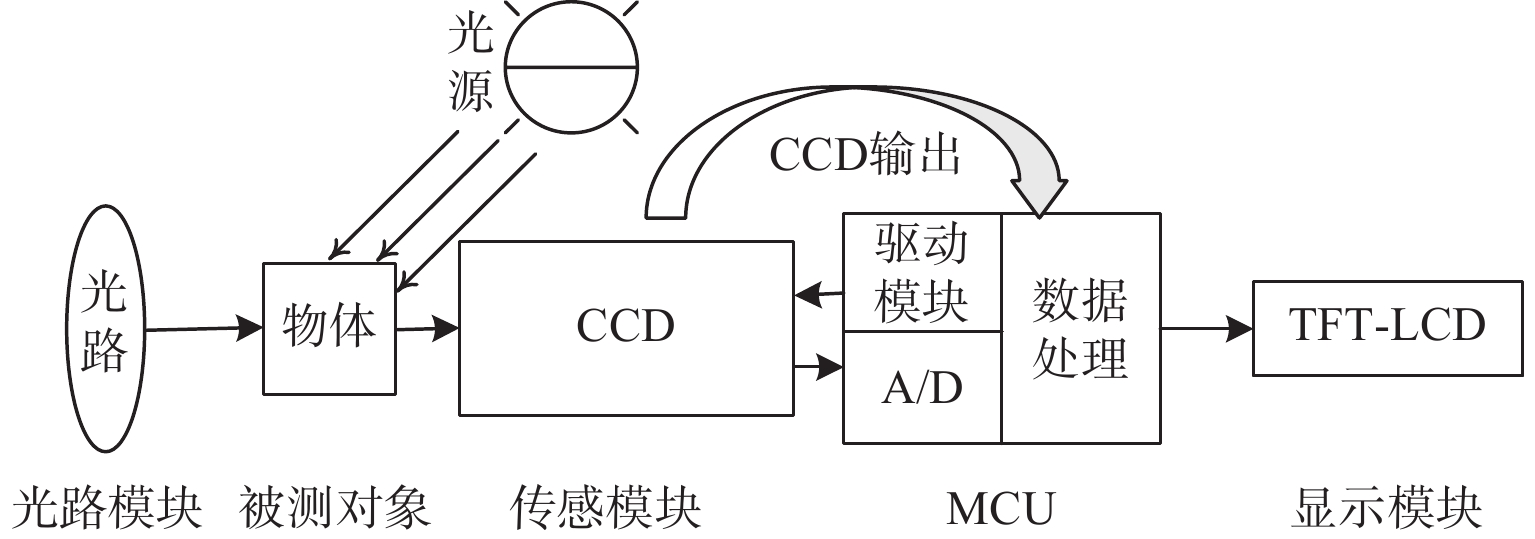
    如图1所示，二维坐标测量系统主要由被测对象、光源、光路模块、传感模块、单片机（microcontroller unit, MCU）和显示模块组成。二维坐标测量系统将光电技术结合，在外部光源照射的条件下，光路模块发射光信号到被测物体表面，采集模块检测到物体表面反射的光线并将采集的数据传输给单片机，单片机对数据进行处理和算法运算，最终得到被测对象的二维坐标信息并在显示模块上面显示。

    图  1  二维坐标测量系统总体框图
    Figure  1.  Overall block diagram of two-dimensional coordinate measurement system
    下载: 全尺寸图片 幻灯片

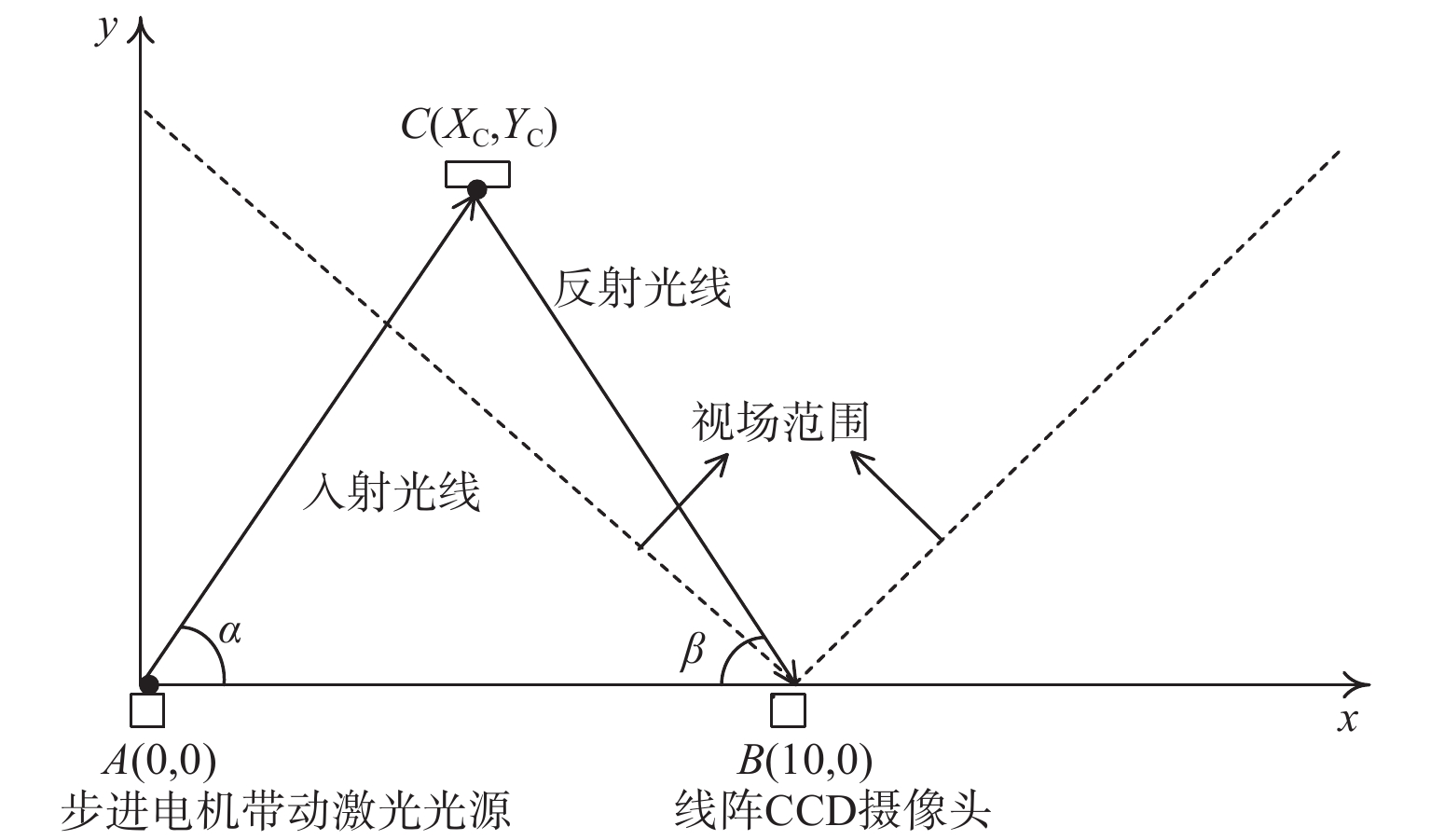
    二维坐标测量系统采用角度交会法对被测对象进行坐标计算。角度交会法是一种通过角度的测量，进而得到未知坐标的算法，具有测量算法公式简单、系统结构装置简易及测量精度较高的特点。如图2所示，A点放置位置为固定的步进电机带动激光光源，B点放置位置为固定的线阵CCD图像传感器，C点为被测对象的位置。假设点A、B和C的坐标依次为（XA,YA）、（XB,YB）和（XC,YC），A点和B点坐标已知，若要求解C点的坐标，则需要测量角$ \alpha $和$ \beta $的大小，然后应用式（1）得到C点坐标：

    $$ \left\{\begin{array}{l} X_{C}=\dfrac{X_{B} \cdot \tan \beta}{\tan \alpha+\tan \beta} \\ Y_{C}=\dfrac{X_{B} \cdot \tan \beta \cdot \tan \alpha}{\tan \alpha+\tan \beta} \end{array} \right.$$ (1)
    图  2  角度交会法求解坐标示意图
    Figure  2.  Schematic diagram of solving coordinates by angle intersection method
    下载: 全尺寸图片 幻灯片

    在图2中，AC为入射光线，CB为反射光线，$ \alpha $角度的大小可以通过步进电机的转动角来测得，$ \beta $角度的大小可以通过线阵CCD输出的信号处理得到，采用角度交会法便可以求解出三角模型中C点的坐标。

    2   硬件设计

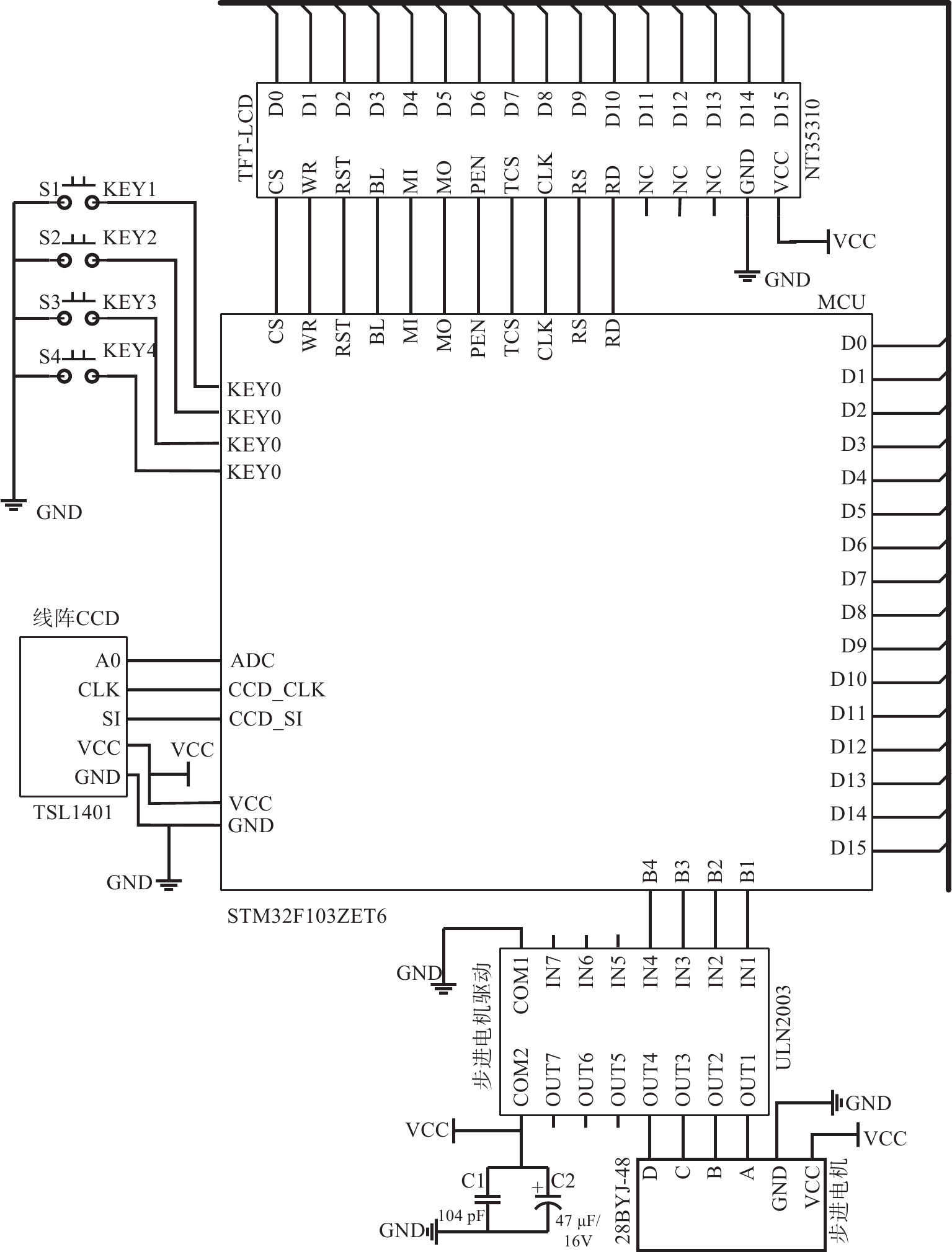
    测量系统采用STM32F103ZET6单片机，核心芯片为STM32F103ZET6；传感模块采用TSL1401线阵CCD图像传感器，选用90°广角镜头；显示模块采用NT35310 TFT-LCD显示屏；同时采用28BYJ-48步进电机和ULN2003步进电机驱动，以满足测量系统设计精度的需求。系统电路原理如图3所示。

    图  3  系统电路原理图
    Figure  3.  Schematic diagram of system circuit
    下载: 全尺寸图片 幻灯片

    MCU驱动线阵CCD图像传感器和显示模块工作，ULN2003步进电机驱动步进电机工作。MCU利用STM32的定时器中断功能编写线阵CCD的驱动时序，无需外加AD转换模块就可以实现将线阵CCD图像传感器采集的信号从模拟信号转换为数字信号。STM32使用FSMC驱动TFT-LCD显示屏，实现显示模块的显示功能。因单片机引脚输出电压过低无法驱动步进电机，所以采用ULN2003步进电机驱动和外设电源的方案，通过MCU将电信号传输给ULN2003，间接实现驱动步进电机的功能。测量系统的各个模块相互配合，完成数据的采集、处理和运算，并对二维坐标进行实时显示。

    3   软件设计

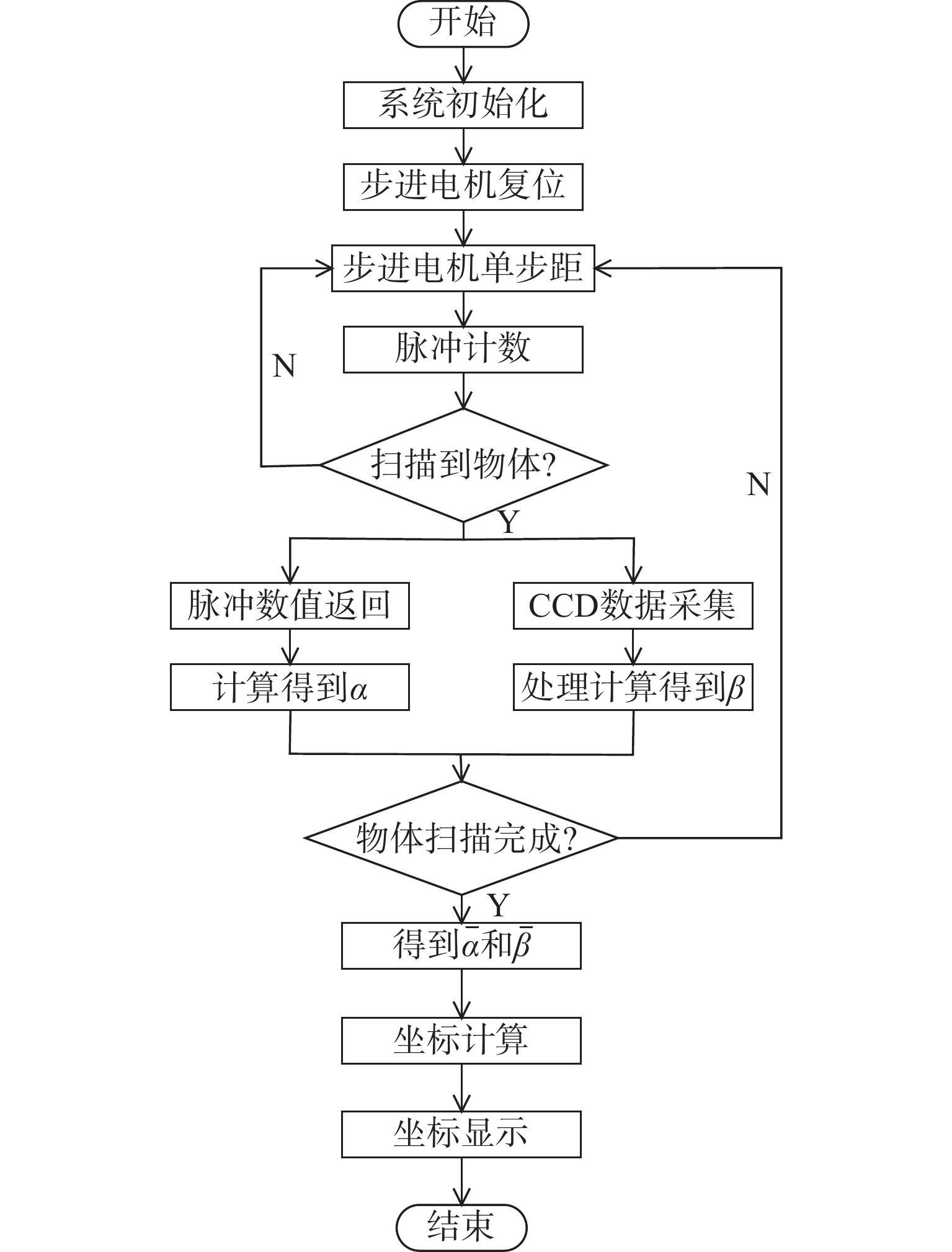
    软件设计部分主要是MCU对步进电机转动、线阵CCD图像传感器数据采集和TFT-LCD显示进行控制，经运算处理得到相关参数，从而得到被测对象的坐标并显示。MCU控制步进电机转动设定角度，从而带动激光光源转动并扫描平面内障碍物；MCU驱动线阵CCD图像传感器实时采集视场范围内的状况，并将采集的信息转化为电信号传输到MCU进行处理得到相关参数；运算处理得到二维坐标，驱动TFT-LCD显示被测对象的坐标信息。在MCU和外部设备相互配合下，完成实验设定条件的控制、数据采集、数据处理、数据计算和结果显示。该系统的主程序流程图如图4所示。

    图  4  主程序流程图
    Figure  4.  Flow chart of master program
    下载: 全尺寸图片 幻灯片

    由图4可知，系统上电后进行初始化，步进电机复位并开始运行程序；步进电机带动激光光源以单位脉冲周期$ 5.625 / 64^{\circ} $的步距角进行转动，并对脉冲数进行计数；当激光光源扫描到被测物时，实时返回脉冲数并计算此时的角度$ \alpha $，此时线阵CCD对被测对象进行数据采集并处理计算得到角度$ \beta $，若未扫描到被测对象，步进电机仍旧以单位脉冲步距角带动激光光源转动直至扫描到被测对象；当被测对象扫描完成时，单片机计算得到角度$ \alpha $和$ \beta $的期望，通过运算处理得到被测对象的坐标，最终在TFT-LCD显示屏上显示，若被测对象未完成扫描，步进电机继续带动激光光源进行扫描直至完成被测对象的扫描。

    3.1   CCD驱动及采集

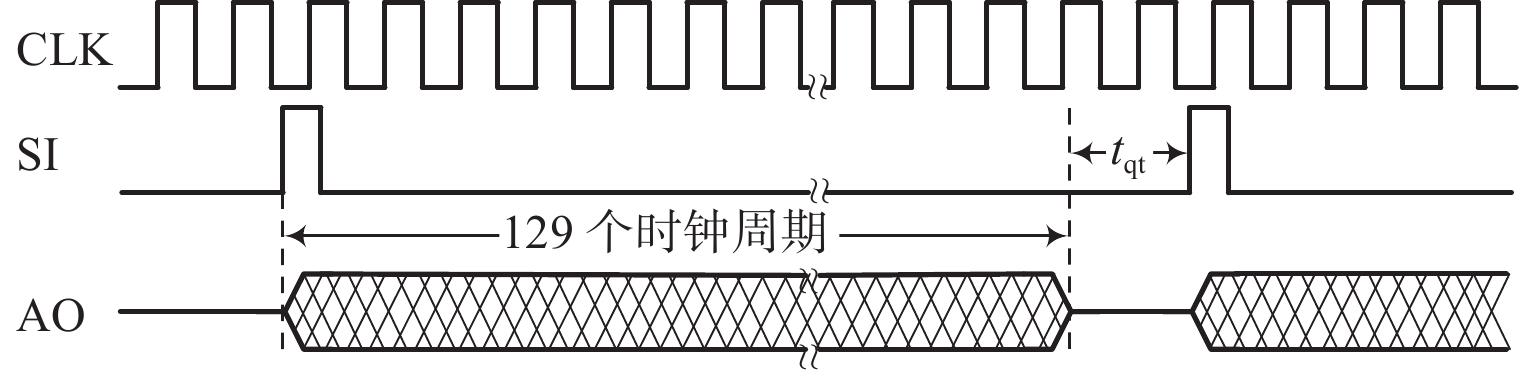
    利用STM32定时器完成TSL1401线阵CCD图像传感器驱动时序。线阵CCD包含128个感光单元，tqt为采样周期间隔，驱动时序图如图5所示。采用时钟管脚PA7产生CLK信号，IO串口PA6作为SI信号输入，从而输出模拟信号AO[12]。

    图  5  TSL1401线阵CCD驱动时序图
    Figure  5.  Drive time-sequence diagram of TSL1401 linear array CCD
    下载: 全尺寸图片 幻灯片

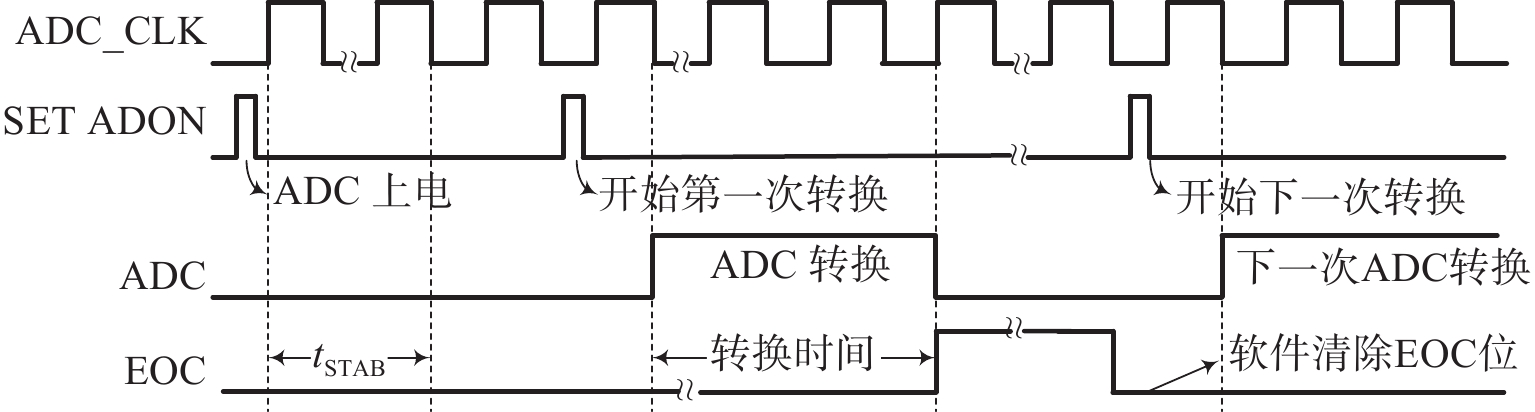
    利用STM32的定时器来触发ADC的启动转换[13]。系统使用单次单通道ADC1触发时序图如图6所示，tSTAB为上电延时；ADC_CLK为ADC1时钟；SET ADON为设置ADC_CR寄存器的ADON位；EOC为规则组转换结束事件标志。设置PA1为模拟输入，通过RCC_CFGR设置ADC1分频因子，最终完成ADC1的模式配置，实现单次转换模式、触发方式选择、数据对齐方式等功能。

    图  6  ADC驱动时序图
    Figure  6.  Drive time-sequence diagram of ADC
    下载: 全尺寸图片 幻灯片

    3.2   步进电机驱动

    如图7所示，系统选用四相八拍的28BYJ48步进电机，对步进电机施加一系列特定顺序并且连续不断地控制脉冲时，便可以连续不断地转动。每个脉冲信号使得步进电机的一相或两相绕组的通电状态改变一次，即转子转过一定角度，当通电状态的改变完成1个循环时，转子转过1个步距角。所以启动步进电机，只需要依次给各个相输入高电平信号。系统采用八拍方式驱动，STM32的4个GPIO串口依次与步进电机驱动的IN1-IN4端口连接，即STM32的PC6、PC7、PC8和PC9串口配置为I/O口，类似PC9、PC8、PC7和PC6这4个端口的输出信号，可以实现对步进电机启动、停止、正转和反转的控制。

    图  7  步进电机驱动时序
    Figure  7.  Drive time-sequence diagram of stepper motor
    下载: 全尺寸图片 幻灯片

    3.3   CCD标定及$\;{\beta} $ 计算

    采用双直线法标定线阵CCD。如图8所示，在线阵CCD图像传感器的视场范围内进行位置标定，在二维坐标测量扫描区的远近平行位置$Y_{{\rm{F}}}$和$Y_{{\rm{N}}}$处对线阵CCD标定采样，其中$Y_{{\rm{F}}}$和$Y_{{\rm{N}}}$为线阵CCD标定的2条采样直线，并且$ \angle M_{i} $和$ \angle N_{i} $ 与$ \beta $相等；假设被测物体在$ m_{i} $和$ n_{i} $点时，线阵CCD图像传感器检测$ m_{i} $和$ n_{i} $点的反射光线重合，则线阵CCD产生的输出信号也相同，可以据此对线阵CCD标定。在远位置$Y_{{\rm{F}}}$上取等间距的20个采样点，将被测对象依次放在采样点处，线阵CCD图像传感器进行数据采集，微控制单元对线阵CCD采集的数据进行处理得到采样点CCD的像元值$ {C_{{x_i}}} $。采用同样的方法对近位置$Y_{{\rm{N}}}$处进行标定采样，因为$ m_{i} $和$ n_{i} $点处进入线阵CCD的入射角$ \angle M_{i} $和$ \angle N_{i} $相等，即可以根据已得的像元值进一步找到$ n_{i} $点。相反，已知$ m_{i} $和$ n_{i} $点的坐标，可以得到$ M_{i} $和$ N_{i} $角度的大小，即可以得到像元值$ {C_{{x_i}}} $与$ \angle M_{i} $和$ \angle N_{i} $ 一一对应的关系。取像元值$ {C_{{x_i}}} $为横坐标, $ \angle M_{i} $和$ \angle N_{i} $为纵坐标，可以得到关于$ {C_{{x_i}}} $与$ \angle M_{i} $和$ \angle N_{i} $的散点图，采用最小二乘法对数据进行拟合，得到$ {C_{{x_i}}} $与$ \angle M_{i} $ 和$ \angle N_{i} $的关系式[14]。

    图  8  双直线法标定CCD示意图
    Figure  8.  Schematic diagram of CCD calibration by double-line method
    下载: 全尺寸图片 幻灯片

    如图9所示，标定图案为在白色平板上刻画黑色竖线，相邻竖线间隔可选。首先选用相邻竖线间隔10 mm的标定图案，将标定图案竖直放置于$Y_{{\rm{F}}}=10$ 的直线上，并将最左边边缘线与$ X=0 $对齐；然后，步进电机带动激光光源在设定的速度下转动，激光光源会在被照射的标定图像竖线上形成点$ m_{i} $；之后，线阵CCD图像传感器进行数据采集，并将信号输出给MCU；最后，MCU对输入的信号进行处理，得到点$ m_{i} $对应的平均像元值，并记录实验数据，如表1所示。

    图  9  标定图案
    Figure  9.  Calibration pattern
    下载: 全尺寸图片 幻灯片
    表  1  $ m_{i} $采样点与对应像元值测试数据
    Table  1.  Sampling points $ m_{i} $ and corresponding pixel value test data
    ${\boldsymbol{m} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{m} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{m} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$
    11148721526
    21099661620
    310310621716
    4981154189
    5911245195
    6841340200
    7781432
    下载: 导出CSV 
    | 显示表格

    选用相邻竖线间隔5 mm的标定图案，将标定图案竖直放置于$Y_{{\rm{N}}}=5$MT4 的直线上，重复上述操作，得到点$ n_{i} $对应的平均像元值，并进行记录，如表2所示。

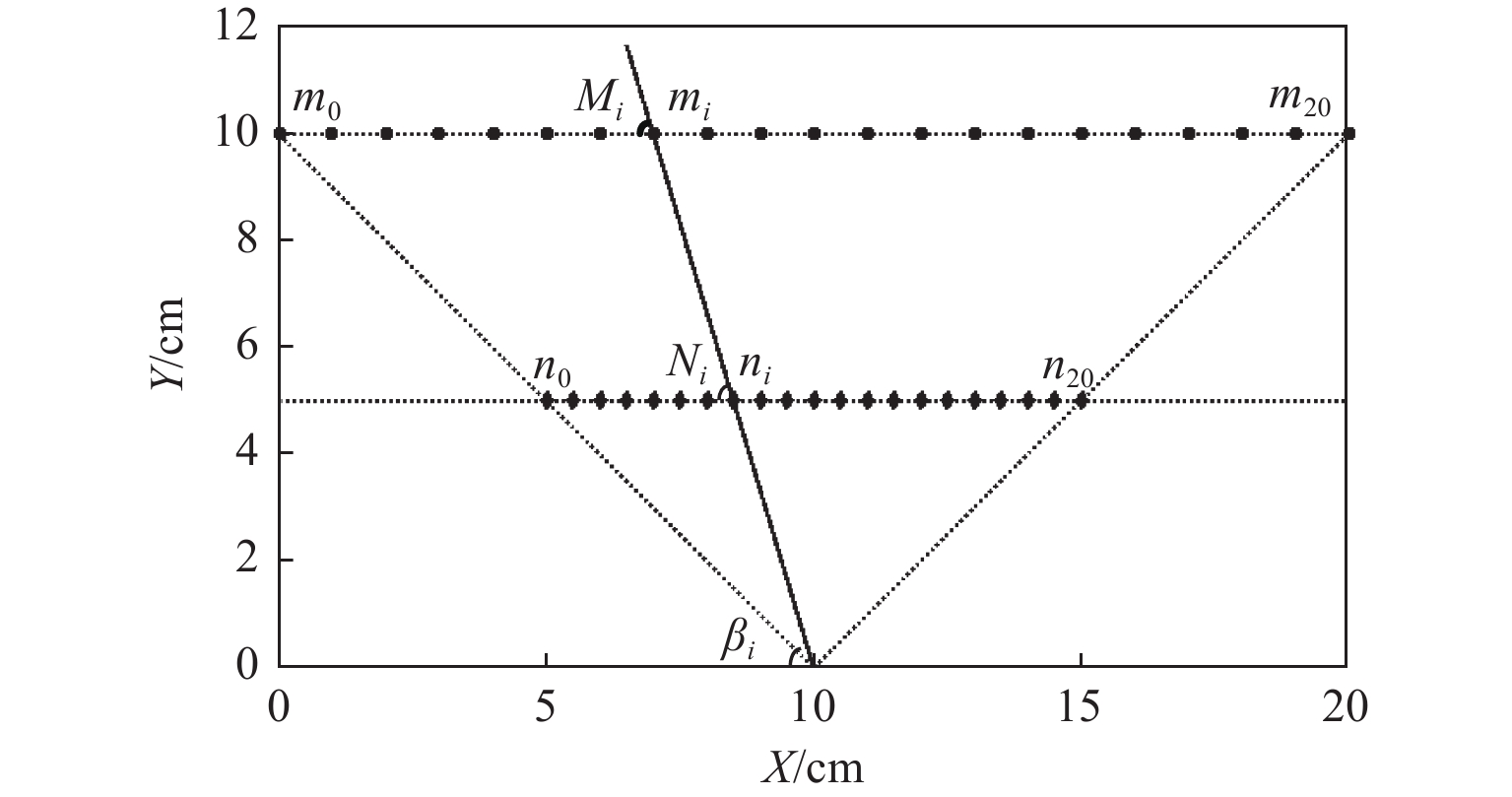
    表  2  $ n_{i} $采样点与对应像元值测试数据
    Table  2.  Sampling points $ n_{i} $ and corresponding pixel value test data
    ${\boldsymbol{n} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{n} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{n} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$
    5.008.57812.033
    5.51149.07212.526
    6.01089.56613.020
    6.510310.06113.515
    7.09810.55414.09
    7.59011.04514.55
    8.08411.54015.01
    下载: 导出CSV 
    | 显示表格

    对比表1和表2可知，点$ n_{i} $对应的像元值几乎可以与点$ m_{i} $对应的像元值一一对应。利用Matlab将上述的2个表格中的点$ m_{i} $和$ n_{i} $描绘在直角坐标系中，如图10所示，并做相关的辅助线，线阵CCD采集$ m_{i} n_{i} $线段上点的像元值输出基本相同，即$ m_{i} n_{i} $线段上点对应的像元值相同，证明采用双直线标定线阵CCD是成立的。

    图  10  $ m_{i} $和$ n_{i} $采样点展示图
    Figure  10.  Display diagram of sampling points $ m_{i} $ and $ n_{i} $
    下载: 全尺寸图片 幻灯片

    $Y_{{\rm{F}}}=10$和$Y_{{\rm{N}}}=5$ 的采样点$ m_{i} $和$ n_{i} $坐标已知，由式（2）计算得$ \angle M_{i} $和$\angle N_{i}$的大小，因$ \angle M_{i} $和$\angle N_{i}$与$ \beta_{i} $相等，即求得$ \beta_{i} $的大小。由表1和表2计算线段$ m_{i} n_{i} $与X轴的夹角$ \beta_{i} $，并将$ \beta_{i} $和相应的像元值记录如表3所示。

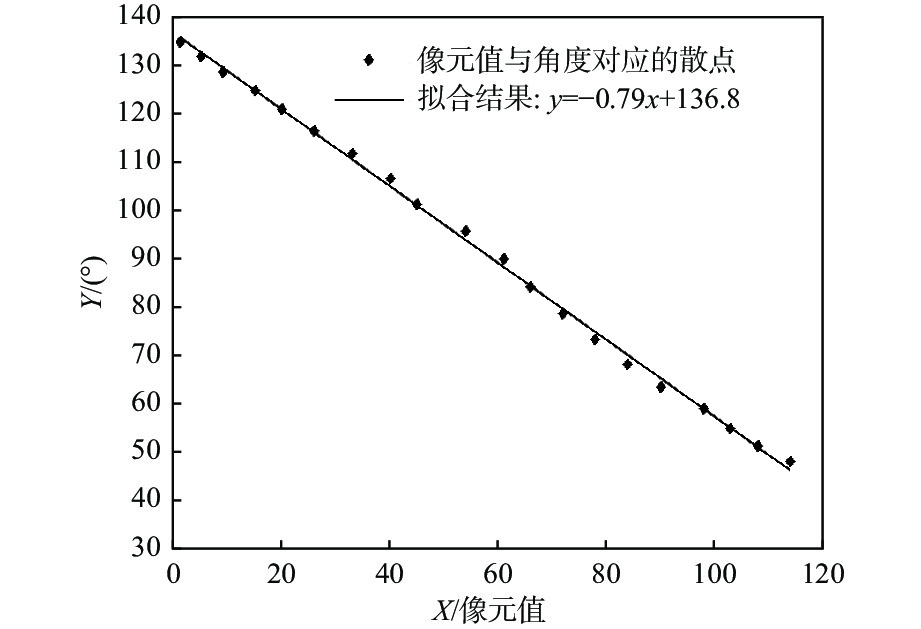
    表  3  像元值与对应$ \beta_{i} $数据
    Table  3.  Image value and the corresponding $ \beta_{i} $ data
    $ {C_{{x_i}}} $$ {{\boldsymbol{\beta}} _{\boldsymbol{i}}} $$ {C_{{x_i}}} $$ {{\boldsymbol{\beta}} _{\boldsymbol{i}}} $$ {C_{{x_i}}} $$ {{\boldsymbol{\beta}} _{\boldsymbol{i}}} $
    045.07873.332111.8
    11448.07278.826116.6
    10851.36684.320121.0
    10355.06190.015125.0
    9859.05495.79128.7
    9063.445101.35132.0
    8468.240106.71135.0
    下载: 导出CSV 
    | 显示表格
    $$ \begin{array}{l} \tan \left(\angle M_{i}\right)=\tan \left(\angle N_{i}\right)=-\left(\dfrac{Y_{m_i}-Y_{n_i}}{X_{m_i}-X_{n_i}}\right) \\ \tan \left(\beta_{i}\right)=-\left(\dfrac{Y_{m_i}}{X_{m_i}-10}\right) \end{array} $$ (2)

    将像元值${C_{{x_i}}}$作为横坐标，$ \beta_{i} $作为纵坐标绘制相应的散点图，利用Matlab进行线性拟合如图11所示。设${\beta _i}=a \cdot {C_{{x_i}}}+b$，最小二乘法线性回归方程如式（3）所示，即$ \beta_{i} $与像元值的关系式为

    $$ \beta_{i}=-0.79{C_{{x_i}}}+136.8 $$ (3)

    式中：

    $$ a=\frac{N \cdot \displaystyle\sum\limits_{i=1}^{N} x_{i} y_{i}-\left(\displaystyle\sum\limits_{i=1}^{N} x_{i}\right) \cdot\left(\displaystyle\sum\limits_{i=1}^{N} y_{i}\right)}{N \cdot \displaystyle\sum\limits_{i=1}^{N} x_{i}^{2}-\left(\displaystyle\sum\limits_{i=1}^{N} x_{i}\right)^{2}}=-0.79 $$ (4)
    $$ b=\frac{\left(\displaystyle\sum\limits_{i=1}^{N} x_{i}^{2}\right) \cdot\left(\displaystyle\sum\limits_{i=1}^{N} y_{i}\right)-\left(\displaystyle\sum\limits_{i=1}^{N} x_{i}\right) \cdot\left(\displaystyle\sum\limits_{i=1}^{N} x_{i} y_{i}\right)}{N \cdot \displaystyle\sum\limits_{i=1}^{N} x_{i}^{2}-\left(\displaystyle\sum\limits_{i=1}^{N} x_{i}\right)^{2}}=136.8 $$ (5)
    图  11  $ \beta_{i} $与像元值的最小二乘法线性回归方程拟合图
    Figure  11.  $ \beta_{i} $ and least square linear regression equation for pixel values
    下载: 全尺寸图片 幻灯片

    3.4   坐标测量算法

    被测对象在线阵CCD图像传感器的视场范围内，步进电机带动激光光源装置放置于原点(0,0)，线阵CCD图像传感器放置于点(10,0)处，MCU直接控制步进电机的转动，间接调整激光光源与X轴夹角的变化。步进电机的转角即就是激光光源的转角，选用型号为28BYJ-48、步距角为$ 5.625 / 64^{\circ} $、额定电压为5V的步进电机，步进电机转动的角度等于脉冲个数与步距角的乘积且与$ \alpha $互余，如式（6）所示：

    $$ \alpha=90-N \cdot 5.625 / 64^{\circ} $$ (6)

    由式（3）和式（6）可得入射光线和反射光线的方程式。

    入射光线方程式：

    $$ Y_{C}=X_{C} \cdot \tan (\alpha)=X_{C} \cdot \tan \left(90-N \cdot 5.625 / 64^{\circ}\right) $$ (7)

    反射光线方程式：

    $$ \begin{split} Y_{C}=&-\left(X_{C}-10\right) \cdot \tan \left(\beta\right)=-\left(X_{C}-10\right) \cdot\\ & \tan \left(-0.79 {C_{{x_i}}}+136.8\right) \end{split} $$ (8)

    由式（6）和式（7）联合求解，得XC与像元值的关系式：

    $$ \begin{split} X_{C}=&\frac{10 \cdot \tan \left(\beta_{i}\right)}{\tan (\alpha)+\tan \left(\beta_{i}\right)}=\\ &\frac{10 \cdot \tan \left(-0.79 {C_{{x_i}}}+136.8\right)}{\tan \left(90-N \cdot 5.625 / 64^{\circ}\right)+\tan \left(-0.79 {C_{{x_i}}}+136.8\right)} \end{split} $$ (9)

    由式（6）和式（8）联合求解，得YC与像元值的关系式：

    $$ \begin{split} &Y_{C}=\frac{10 \cdot \tan \left(\beta_{i}\right) \cdot \tan (\alpha)}{\tan (\alpha)+\tan \left(\beta_{i}\right)}=\\ &\frac{10 \cdot \tan \left(-0.79 {C_{{x_i}}}+136.8\right) \cdot \tan \left(90-N \cdot 5.625 / 64^{\circ}\right)}{\tan \left(90-N \cdot 5.625 / 64^{\circ}\right)+\tan \left(-0.79 {C_{{x_i}}}+136.8\right)} \end{split} $$ (10)

    4   测试结果及分析

    二维坐标图像测量系统如图12所示，采用控制变量法分别对X轴和Y轴坐标进行分析。将被测对象放置于Y=10处，在线阵CCD图像传感器的视野范围内以及X轴坐标准确的前提下，以1 cm为间隔移动被测对象，得到Y轴固定X轴变化的二维坐标，如表4所示。

    图  12  二维坐标图像测量系统
    Figure  12.  Two-dimensional coordinate image measurement system
    下载: 全尺寸图片 幻灯片
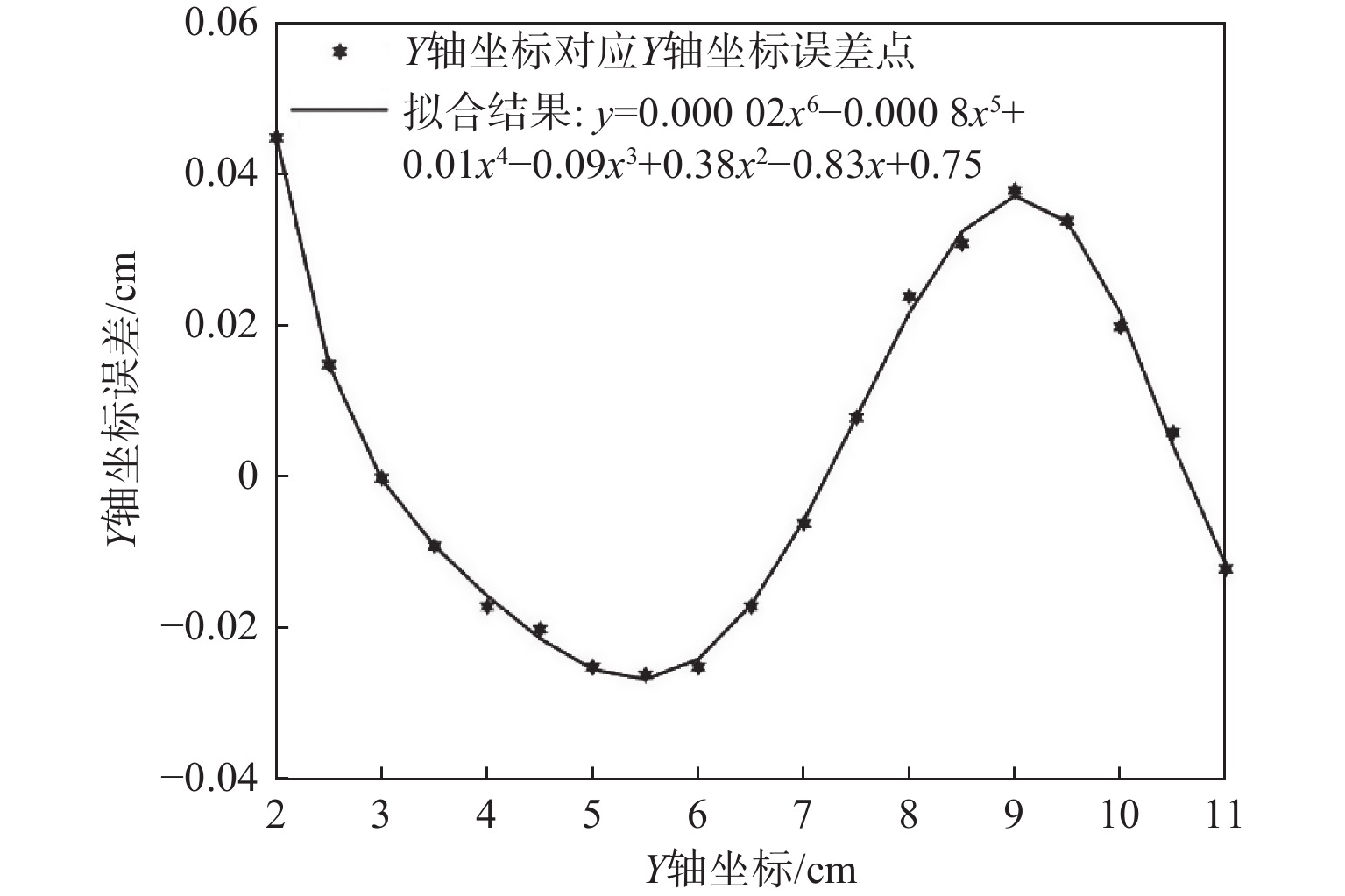
    表  4  Y=10时坐标测量数据
    Table  4.  Coordinate test data when Y=10
    $ {\boldsymbol{Y}} $$ {\boldsymbol{X}} $${\boldsymbol{Y} }_{ {{\rm{test}} } }$$ {\boldsymbol{X}} $${\boldsymbol{Y} }_{ {{\rm{test}} } }$$ {\boldsymbol{X}} $${\boldsymbol{Y} }_{ {{\rm{test}} } }$
    10110.2289.861510.20
    10210.0799.871610.17
    10310.00109.911710.10
    1049.96119.971810.09
    1059.921210.04199.94
    1069.891310.12
    1079.871410.17
    下载: 导出CSV 
    | 显示表格

    计算知Y=10处的测量值$\bar{Y}_{ {{\rm{test}} }}=10.019$，同上测量Y=2至Y=11间隔0.5 cm的直线上的坐标，并对数据进行处理，记录如表5所示。对Y轴坐标的测量误差进行多项式线性拟合，得到如图13所示的Y轴坐标测量值误差的拟合多项式误差曲线[15]。误差曲线的6次项和5次项系数比较小可以忽略，误差曲线可以表示为$y=0.01 x^{4}-0.09 x^{3}+0.38 x^{2}- 0.83 x+0.75$，即可以取Y轴坐标测量值误差的拟合曲线的相反数作为修正值，则被测对象的Y轴修正坐标为

    $$ \begin{split} {Y_i} = & \frac{{10 \cdot \tan \left( { - 0.79{C_{{x_i}}} + 136.8} \right) \cdot \tan \left( {90 - N \cdot 5.625/{{64}^{\circ} }} \right)}}{{\tan \left( {90 - N \cdot 5.625/{{64}^{\circ} }} \right) + \tan \left( { - 0.79{C_{{x_i}}} + 136.8} \right)}} -\\ &0.01{x^4} + 0.09{x^3} - 0.38{x^2} + 0.83x - 0.75 \end{split}$$
    表  5  不同Y轴坐标测量数据
    Table  5.  Different Y-axis coordinate measurement data
    $ {\boldsymbol{Y}} $$\bar{\boldsymbol{Y} }_{ {{\rm{test}} } }$$ \Delta {\boldsymbol{Y}} $$ {\boldsymbol{Y}} $$\bar{\boldsymbol{Y} }_{ {{\rm{test}} } }$$ \Delta {\boldsymbol{Y}} $
    2.02.0450.0457.06.994−0.006
    2.52.5150.0157.57.5080.008
    3.03.0000.0008.08.0240.024
    3.53.491−0.0098.58.5310.031
    4.03.983−0.0179.09.0380.038
    4.54.481−0.0209.59.5340.034
    5.04.975−0.02510.010.0200.020
    5.55.474−0.02610.510.5060.006
    6.05.975−0.02511.010.988−0.012
    6.56.483−0.017
    下载: 导出CSV 
    | 显示表格
    图  13  Y轴坐标的测量误差多项式拟合曲线图
    Figure  13.  Polynomial fitting curve of measurement error for Y-axis coordinates
    下载: 全尺寸图片 幻灯片

    同上操作，测量X=2至X=19间隔1 cm的直线上的坐标，对X轴坐标进行分析处理如表6所示。

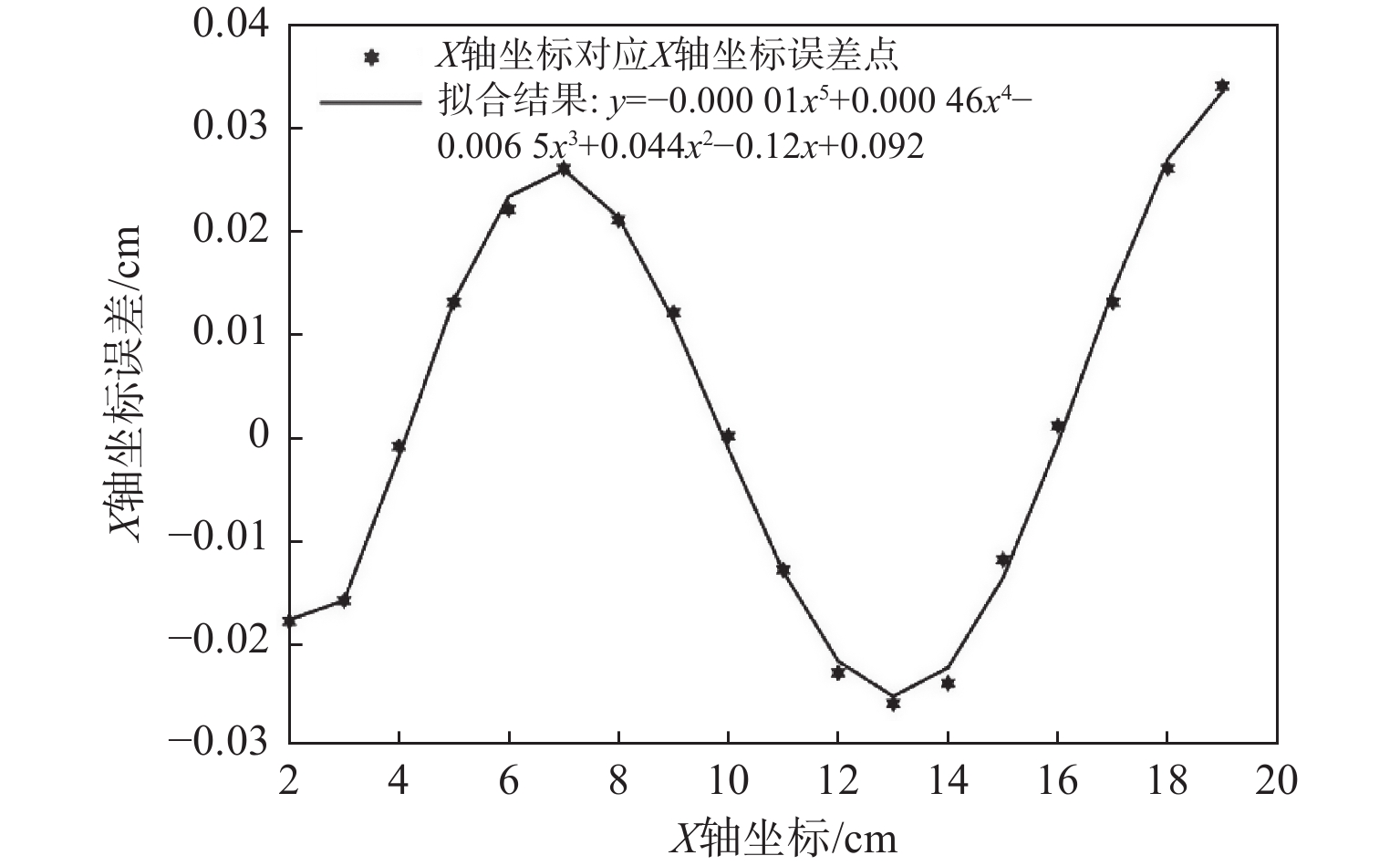
    表  6  不同X轴坐标测量数据
    Table  6.  Different X-axis coordinate measurement data
    $ {{\boldsymbol{X}}} $$\overline{ { {\boldsymbol{X} } } }_{{\rm{test}}}$$ \Delta {{\boldsymbol{X}}} $$ {{\boldsymbol{X}}} $$\overline{ { {\boldsymbol{X} } } }_{{\rm{test}}}$$ \Delta {{\boldsymbol{X}}} $
    21.982−0.0181110.987−0.013
    32.984−0.0161211.977−0.023
    43.999−0.0011312.974−0.026
    55.0130.0131413.976−0.024
    66.0220.0221514.988−0.012
    77.0260.0261616.0010.001
    88.0210.0211717.0130.013
    99.0120.0121818.0260.026
    1010.000.0001919.0340.034
    下载: 导出CSV 
    | 显示表格

    同上操作，误差曲线的5次项系数比较小可以忽略，如图14所示，误差曲线可以表示为$y= 0.004\;6 x^{4}-0.006\;5 x^{3}+0.044 x^{2}-0.12 x+0.092$，即被测对象的X轴修正坐标为

    $$ \begin{split} {X_i} = &\frac{{10 \cdot \tan \left( { - 0.79{C_{{x_i}}} + 136.8} \right)}}{{\tan \left( {90 - N \cdot 5.625/{{64}^{\circ} }} \right) + \tan \left( { - 0.79{C_{{x_i}}} + 136.8} \right)}} -\\ &0.000\;46{x^4} + 0.006\;5{x^3} - 0.044{x^2} + 0.12x - 0.092 \end{split}$$
    图  14  X轴坐标的测量误差多项式拟合曲线图
    Figure  14.  Polynomial fitting curve of measurement error for X-axis coordinates
    下载: 全尺寸图片 幻灯片

    将上述X轴和Y轴坐标修正公式加入系统程序，得到如图15所示的点(5,6)坐标的测量结果。与未修正的坐标测量结果对比，可知修正后的坐标测量结果误差减小了一些，X轴坐标误差由−0.006 0 cm减小到−0.001 3 cm，Y轴坐标误差由−0.039 9 cm减小到−0.010 4 cm，即这样的坐标修正方法是可行的。

    图  15  二维坐标测量结果展示图
    Figure  15.  Display of 2D coordinate measurement results
    下载: 全尺寸图片 幻灯片

    5   结论

    基于角度交会法设计了一种二维坐标图像测量系统，分析处理测量结果得到修正公式，进而修正坐标计算公式提高坐标测量精度。系统采用线阵CCD图像传感器为传感模块，发挥线阵CCD大视野、高扫描频率、高分辨率的特点，能够准确、快速、可靠的采集被测对象的信息；搭建三角测距光路模型，测量两个角度参数，采用角度交会法计算二维坐标；利用Matlab分别分析处理X轴坐标和Y轴坐标，对坐标测量误差进行多项式拟合，得到坐标修正公式，并将其应用于坐标计算，实验测量结果表明修正后的系统测量精度更高。

  • 图  1   二维坐标测量系统总体框图

    Figure  1.   Overall block diagram of two-dimensional coordinate measurement system

    下载: 全尺寸图片 幻灯片

    图  2   角度交会法求解坐标示意图

    Figure  2.   Schematic diagram of solving coordinates by angle intersection method

    下载: 全尺寸图片 幻灯片

    图  3   系统电路原理图

    Figure  3.   Schematic diagram of system circuit

    下载: 全尺寸图片 幻灯片

    图  4   主程序流程图

    Figure  4.   Flow chart of master program

    下载: 全尺寸图片 幻灯片

    图  5   TSL1401线阵CCD驱动时序图

    Figure  5.   Drive time-sequence diagram of TSL1401 linear array CCD

    下载: 全尺寸图片 幻灯片

    图  6   ADC驱动时序图

    Figure  6.   Drive time-sequence diagram of ADC

    下载: 全尺寸图片 幻灯片

    图  7   步进电机驱动时序

    Figure  7.   Drive time-sequence diagram of stepper motor

    下载: 全尺寸图片 幻灯片

    图  8   双直线法标定CCD示意图

    Figure  8.   Schematic diagram of CCD calibration by double-line method

    下载: 全尺寸图片 幻灯片

    图  9   标定图案

    Figure  9.   Calibration pattern

    下载: 全尺寸图片 幻灯片

    图  10   $ m_{i} $和$ n_{i} $采样点展示图

    Figure  10.   Display diagram of sampling points $ m_{i} $ and $ n_{i} $

    下载: 全尺寸图片 幻灯片

    图  11   $ \beta_{i} $与像元值的最小二乘法线性回归方程拟合图

    Figure  11.   $ \beta_{i} $ and least square linear regression equation for pixel values

    下载: 全尺寸图片 幻灯片

    图  12   二维坐标图像测量系统

    Figure  12.   Two-dimensional coordinate image measurement system

    下载: 全尺寸图片 幻灯片

    图  13   Y轴坐标的测量误差多项式拟合曲线图

    Figure  13.   Polynomial fitting curve of measurement error for Y-axis coordinates

    下载: 全尺寸图片 幻灯片

    图  14   X轴坐标的测量误差多项式拟合曲线图

    Figure  14.   Polynomial fitting curve of measurement error for X-axis coordinates

    下载: 全尺寸图片 幻灯片

    图  15   二维坐标测量结果展示图

    Figure  15.   Display of 2D coordinate measurement results

    下载: 全尺寸图片 幻灯片

    表  1   $ m_{i} $采样点与对应像元值测试数据

    Table  1   Sampling points $ m_{i} $ and corresponding pixel value test data

    ${\boldsymbol{m} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{m} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{m} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$
    11148721526
    21099661620
    310310621716
    4981154189
    5911245195
    6841340200
    7781432
    下载: 导出CSV

    表  2   $ n_{i} $采样点与对应像元值测试数据

    Table  2   Sampling points $ n_{i} $ and corresponding pixel value test data

    ${\boldsymbol{n} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{n} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$${\boldsymbol{n} }_{ {\boldsymbol{i} } }\_{ {\boldsymbol{X} } }_{ {\boldsymbol{i} } }$${C_{{x_i}}}$
    5.008.57812.033
    5.51149.07212.526
    6.01089.56613.020
    6.510310.06113.515
    7.09810.55414.09
    7.59011.04514.55
    8.08411.54015.01
    下载: 导出CSV

    表  3   像元值与对应$ \beta_{i} $数据

    Table  3   Image value and the corresponding $ \beta_{i} $ data

    $ {C_{{x_i}}} $$ {{\boldsymbol{\beta}} _{\boldsymbol{i}}} $$ {C_{{x_i}}} $$ {{\boldsymbol{\beta}} _{\boldsymbol{i}}} $$ {C_{{x_i}}} $$ {{\boldsymbol{\beta}} _{\boldsymbol{i}}} $
    045.07873.332111.8
    11448.07278.826116.6
    10851.36684.320121.0
    10355.06190.015125.0
    9859.05495.79128.7
    9063.445101.35132.0
    8468.240106.71135.0
    下载: 导出CSV

    表  4   Y=10时坐标测量数据

    Table  4   Coordinate test data when Y=10

    $ {\boldsymbol{Y}} $$ {\boldsymbol{X}} $${\boldsymbol{Y} }_{ {{\rm{test}} } }$$ {\boldsymbol{X}} $${\boldsymbol{Y} }_{ {{\rm{test}} } }$$ {\boldsymbol{X}} $${\boldsymbol{Y} }_{ {{\rm{test}} } }$
    10110.2289.861510.20
    10210.0799.871610.17
    10310.00109.911710.10
    1049.96119.971810.09
    1059.921210.04199.94
    1069.891310.12
    1079.871410.17
    下载: 导出CSV

    表  5   不同Y轴坐标测量数据

    Table  5   Different Y-axis coordinate measurement data

    $ {\boldsymbol{Y}} $$\bar{\boldsymbol{Y} }_{ {{\rm{test}} } }$$ \Delta {\boldsymbol{Y}} $$ {\boldsymbol{Y}} $$\bar{\boldsymbol{Y} }_{ {{\rm{test}} } }$$ \Delta {\boldsymbol{Y}} $
    2.02.0450.0457.06.994−0.006
    2.52.5150.0157.57.5080.008
    3.03.0000.0008.08.0240.024
    3.53.491−0.0098.58.5310.031
    4.03.983−0.0179.09.0380.038
    4.54.481−0.0209.59.5340.034
    5.04.975−0.02510.010.0200.020
    5.55.474−0.02610.510.5060.006
    6.05.975−0.02511.010.988−0.012
    6.56.483−0.017
    下载: 导出CSV

    表  6   不同X轴坐标测量数据

    Table  6   Different X-axis coordinate measurement data

    $ {{\boldsymbol{X}}} $$\overline{ { {\boldsymbol{X} } } }_{{\rm{test}}}$$ \Delta {{\boldsymbol{X}}} $$ {{\boldsymbol{X}}} $$\overline{ { {\boldsymbol{X} } } }_{{\rm{test}}}$$ \Delta {{\boldsymbol{X}}} $
    21.982−0.0181110.987−0.013
    32.984−0.0161211.977−0.023
    43.999−0.0011312.974−0.026
    55.0130.0131413.976−0.024
    66.0220.0221514.988−0.012
    77.0260.0261616.0010.001
    88.0210.0211717.0130.013
    99.0120.0121818.0260.026
    1010.000.0001919.0340.034
    下载: 导出CSV
    • 参考文献(15)
  • [1] 卢佳宝, 韩学辉, 王彩霞. 基于线阵CCD的精密尺寸测量系统[J]. 光电子·激光,2019,30(9):935-940.

    LU Jiabao, HAN Xuehui, WANG Caixia. Precise dimension measurement system based on linear CCD[J]. Journal of Optoelectronics·Laser,2019,30(9):935-940.
    [2] 宫二敏, 黄强先, 余夫领. 共平面二维高精度工作台误差修正与实验研究[J]. 中国测试,2014,40(4):10-14. doi: 10.11857/j.issn.1674-5124.2014.04.003

    GONG Ermin, HUANG Qiangxian, YU Fuling. Research of error correction and experiment of co-planar 2D high precision stage[J]. China Measurement & Test,2014,40(4):10-14. doi: 10.11857/j.issn.1674-5124.2014.04.003
    [3]

    HOCKEN R J. Coordinate measuring machines and systems[D]. Boca Raton: Crc Press, 2016.
    [4]

    CHEN Z Y, WANG Y C, YANG Y, et al. PSD: principled synthetic-to-real dehazing guided by physical priors[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville: IEEE, 2021: 7180-7189.
    [5] 朱博源, 任永杰, 段显龙, 等. 旋转激光扫描无源多靶点定位方法[J]. 光学学报,2022,42(5):66-76.

    ZHU Boyuan, REN Yongjie, DUAN Xianlong, et al. Passive multi-target location method based on rotating laser scanning[J]. Acta Optica Sinica,2022,42(5):66-76.
    [6]

    LI J, QIN H, WANG J Z, et al. Open street map-based autonomous navigation for the four wheel-legged robot via 3D-lidar and CCD camera[J]. IEEE Transactions on Industrial Electronics,2022,69(3):2708-2717. doi: 10.1109/TIE.2021.3070508
    [7] 白玮本, 曹慧峰, 刘欣宜. 基于结构光的嵌入式图像采集系统[J]. 仪表技术与传感器,2021(8):55-58. doi: 10.3969/j.issn.1002-1841.2021.08.012

    BAI Weiben, CAO Huifeng, LIU Xinyi. Embedded image acquisition system based on structured light[J]. Instrument Technique and Sensor,2021(8):55-58. doi: 10.3969/j.issn.1002-1841.2021.08.012
    [8]

    PAN Y, DONG Y Q, WANG D L, et al. Three-dimensional reconstruction of structural surface model of heritage bridges using UAV-based photogrammetric point clouds[J]. Remote Sensing,2019,11(10):1204. doi: 10.3390/rs11101204
    [9]

    SHAH V, KENIYA R, SHRIDHARANI A, et al. Diagnosis of COVID-19 using CT scan images and deep learning techniques[J]. Emergency Radiology,2021,28(3):497-505. doi: 10.1007/s10140-020-01886-y
    [10]

    RUMBOLDT Z, HUDA W, ALL J W. Review of portable CT with assessment of a dedicated head CT scanner[J]. American Journal of Neuroradiology,2009,30(9):1630-1636. doi: 10.3174/ajnr.A1603
    [11] 张同双, 傅敏辉, 钟德安, 等. 基于MLE算法的海上角度交会测量方法及其精度分析[J]. 电讯技术,2013,53(8):1033-1038. doi: 10.3969/j.issn.1001-893x.2013.08.012

    ZHANG Tongshuang, FU Minhui, ZHONG Dean, et al. Marine angle intersection method based on MLE algorithm and its precision analysis[J]. Telecommunication Engineering,2013,53(8):1033-1038. doi: 10.3969/j.issn.1001-893x.2013.08.012
    [12] 田又源, 程瑶, 贾宁, 等. 高速线阵CCD驱动与数据采集系统设计[J]. 仪表技术与传感器,2022(3):84-87. doi: 10.3969/j.issn.1002-1841.2022.03.016

    TIAN Youyuan, CHENG Yao, JIA Ning, et al. Design of high speed linear CCD driving and data acquisition system[J]. Instrument Technique and Sensor,2022(3):84-87. doi: 10.3969/j.issn.1002-1841.2022.03.016
    [13] 高毅, 于瀛, 杨絮, 等. 基于多波段光源的智能痕迹分色方法[J]. 应用光学,2023,44(1):46-54.

    GAO Yi, YU Ying, YANG Xu, et al. Intelligent trace color separation method based on multi-band light source[J]. Journal of Applied Optics,2023,44(1):46-54.
    [14] 伍川辉, 尹纪磊, 郭辉, 等. 基于二维激光位移传感器的通过式轮对测量系统设计[J]. 仪表技术与传感器,2020(11):50-53. doi: 10.3969/j.issn.1002-1841.2020.11.011

    WU Chuanhui, YIN Jilei, GUO Hui, et al. Design of wheel-set measurement system based on two-dimensional laser displacement sensor[J]. Instrument Technique and Sensor,2020(11):50-53. doi: 10.3969/j.issn.1002-1841.2020.11.011
    [15] 顾天奇, 林述温, 陈剑雄, 等. 坐标测量数据稳健拟合算法与实验研究[J]. 机械设计与制造,2019(7):165-167. doi: 10.3969/j.issn.1001-3997.2019.07.041

    GU Tianqi, LIN Shuwen, CHEN Jianxiong, et al. The robust fitting algorithm and experimental study of measurement data of coordinate measurement machine[J]. Machinery Design & Manufacture,2019(7):165-167. doi: 10.3969/j.issn.1001-3997.2019.07.041
    • 相关文章
    • 施引文献(13)

  • 期刊类型引用(8)

    1. 习啸天，韩军，张岩. 一种大视场高分辨率的复眼光学系统设计. 应用光学. 2024(02): 314-320 . 本站查看
    2. 陈炳旭，杨旭，张智强，栾晓宇，蒋锐. 宽波段折反射式航空相机设计. 红外技术. 2024(08): 864-871 . 百度学术
    3. 王跃，刘海英，陈晓宇，朱海滨，杨旭，姜彦名，王英. 基于三线靶标的航空相机地面分辨率质量评价. 光电技术应用. 2024(05): 34-38 . 百度学术
    4. 尹云飞. 航空相机像旋补偿双向控制中的内环补偿器设计. 机械管理开发. 2024(12): 99-101+104 . 百度学术
    5. 刘金沧，黎治坤，王英谋，李翔，郭雨晴. 摆扫式倾斜影像数据处理关键问题研究. 科学技术创新. 2023(08): 17-21 . 百度学术
    6. 吴雄雄，王惠林，宁飞，张文博，刘吉龙，王明超. 大气湍流对航空光电侦察图像质量影响因素分析. 应用光学. 2022(01): 1-8 . 本站查看
    7. 张磊，许慧超，王云，付杨，赵越，汤晓峰，石钰，孙勇，张弦，贾金升. 大口径光纤倒像器制备工艺研究. 应用光学. 2021(04): 735-742 . 本站查看
    8. 邹甜妹，韦晓孝，吕元，万新军，李雪宸，张昊. 面向光学装调微小距离测量的系统设计. 光学仪器. 2021(05): 48-53 . 百度学术

    其他类型引用(5)

    • 资源附件(0)
图(15)  /  表(6)
计量
  • 文章访问数:  84
  • HTML全文浏览量:  17
  • PDF下载量:  33
  • 被引次数: 13
出版历程
  • 收稿日期:  2023-10-18
  • 修回日期:  2024-01-11
  • 网络出版日期:  2024-02-19
  • 刊出日期:  2024-03-14

目录

摘要
HTML全文

  • 引言

  • 1   系统测量原理

  • 2   硬件设计

  • 3   软件设计

  • 3.1   CCD驱动及采集

  • 3.2   步进电机驱动

  • 3.3   CCD标定及$\;{\beta} $ 计算

  • 3.4   坐标测量算法

  • 4   测试结果及分析

  • 5   结论

参考文献(15)
相关文章
施引文献(13)
资源附件(0)

/

返回文章
返回

相关数据库

广告合作

友情链接

帮助中心

扫描关注本刊微信平台

您是第  2926683位访问者，欢迎！

地址: 西安市电子三路西段9号 邮政编码: 710065 联系电话: 029-88288172

版权所有 © 《应用光学》编辑部

陕公网安备 61011302001501号       陕ICP备19002862号-1

北京仁和汇智信息技术有限公司 开发  技术支持: info@rhhz.net   百度统计