Light field refocusing analysis of different interpolation algorithms
-
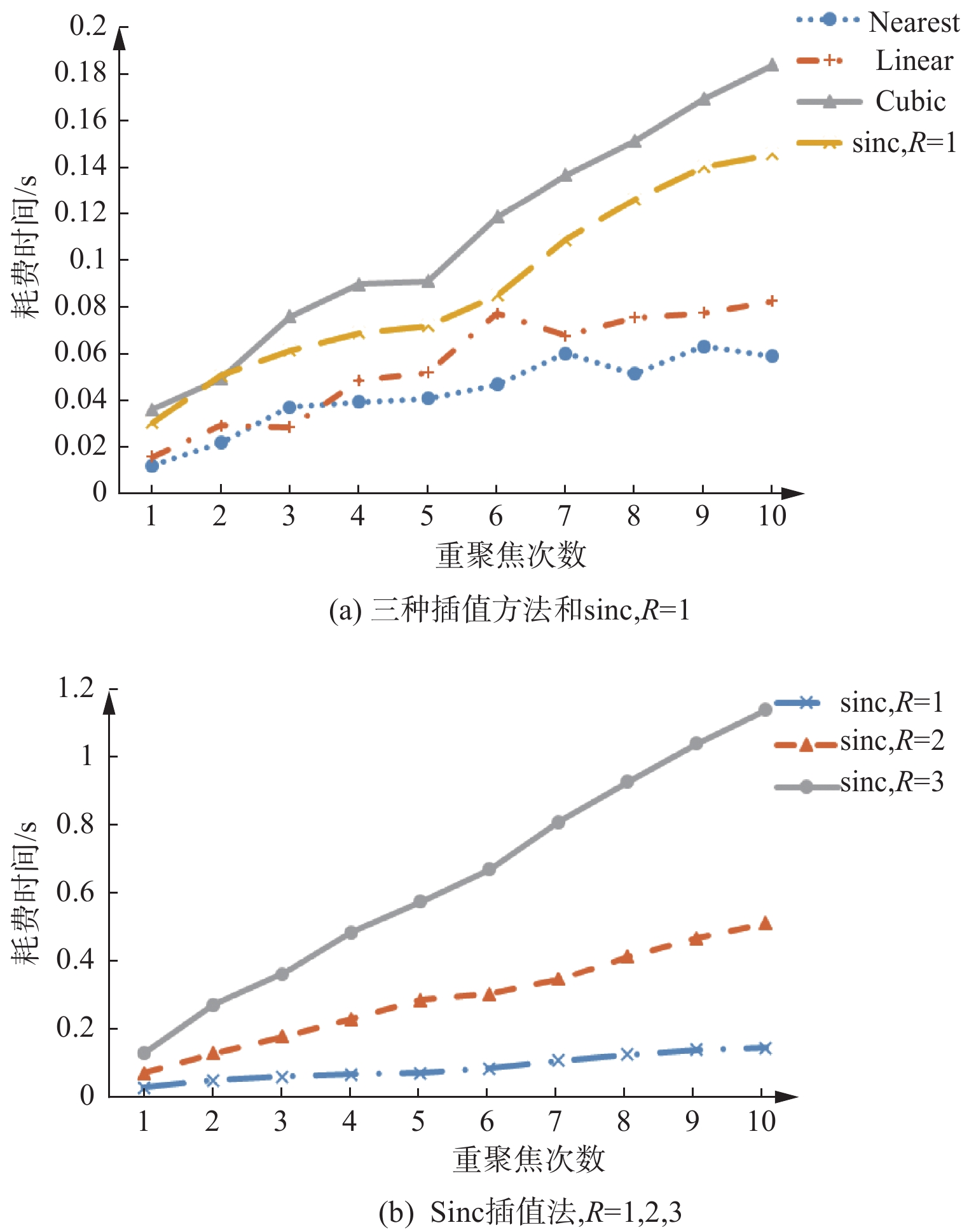
摘要: 光场数据重聚焦包括空间域重聚焦和频域重聚焦两种方法，在重聚焦过程中均需要进行插值计算，重聚焦精度与插值精度密切相关，而插值算法的复杂度会影响计算效率。在实际大量图像处理中，在重聚焦效果满足精度要求的前提下选择计算效率最高的方法，其中，插值精度对频域影响远大于空间域。介绍了空间域重聚焦和频域重聚焦的原理，以及传统3种插值方法和sinc函数插值法，分别用不同的插值方法对这两种重聚焦方法进行实验，比较其重聚焦效果并计算其效率。实验结果表明，在实际应用中为了满足计算效率的需求，在满足精度要求情况下，空间域重聚焦采用线性插值法最佳，频域采用采样半径为2像素的sinc插值最佳。对同一幅影像多次重聚焦时，频域方法优于空间域方法。Abstract: The light field data refocusing includes spatial domain refocusing and frequency domain refocusing. In the process of the refocusing, the interpolation calculation is needed, the refocusing precision is closely related to the interpolation precision, and the computational efficiency can be affected by the complexity of the interpolation algorithm. In the actual large amount of the image processing, the method with the highest computational efficiency is selected under the premise that the refocusing effect satisfies the accuracy requirement, and wherein the interpolation accuracy has a much greater influence on the frequency domain than the spatial domain. The principle of the spatial domain refocusing and the frequency domain refocusing, as well as the traditional three interpolation methods and the sinc function interpolation method were introduced. Different interpolation methods were used to experiment this two refocusing methods to compare their refocusing effect and calculate their efficiency. The experimental results show that in order to meet the requirement of the computational efficiency in actual applications, the linear interpolation method is the best method to optimize the spatial domain refocusing in the case of meeting the accuracy requirement, and the sinc interpolation with the sampling radius of 2 is optimal in the frequency domain. When the same image is refocused for multiple times, the frequency domain method is superior to the spatial domain method.
-
引言
随着数字视频制作技术和数字投影机技术的快速发展，球幕数字投影越来越受到青睐，被广泛应用于天文、地理教学、展览展示等领域[1-3]。然而，市场上数字投影机的品牌和规格繁多，所需要配制的数字鱼眼镜头的规格也很多，检测为数字投影机配制的数字鱼眼镜头便成为了难题。目前，国内外还没有相关的检测设备对数字鱼眼镜头的性能、放映效果进行全面的测试，只能购买价格昂贵的与之匹配的数字投影机来进行性能、放映效果的测试，这样不仅增加了测试费用成本，而且通用性差。为此，研制一种通用型可检测各种类型数字投影鱼眼镜头的检测系统，变得十分迫切。本文研究讨论了一种鱼眼镜头检测系统，可实现芯片尺寸为0.55″~1.55″的1DLP、3DLP、3LCD、3LCOS的各类型的数字投影或放映鱼眼镜头的像方视场角、分辨率、彩色还原性能、色差等性能和放映效果进行测试，通用性强。
1 技术要求
设计一种检测系统，可以满足0.55″~1.55″的1DLP、3DLP、3LCD、3LCOS的各类型的数字投影或放映鱼眼镜头的性能参数和放映效果的测试，可实现的照明视场范围大于φ8.5 mm~φ35 mm，照明视场的照度均匀性应不低于85%，出射光通量应不小于5 000 lm。
2 设计思路
数字鱼眼镜头的设计是根据所配接的数字投影或放映机的关键参数和尺寸而定，如数字鱼眼镜头的像高由芯片尺寸而确定。为了更好地匹配系统整体像差，数字鱼眼镜头在设计时需要加入等效平行平板来模拟数字投影或放映机内部光学引擎中分合色棱镜[4-7]。
要满足不同规格的数字鱼眼镜头的性能(视场角、分辨率、彩色还原性能、色差)和放映效果的测试，检测系统需要具有不同种类和规格的检测标板，同时具有模拟数字投影或放映机内部分合色棱镜的功能，以及具有可以形成均匀且大小尺寸能改变的照明视场的功能。
3 设计过程
3.1 鉴别率标板的设计
数字投影或放映机的分辨率直接决定了所配接的数字鱼眼镜头的极限分辨率[4, 8]，由公式(1)得出：
$$ ~{{R}_{L}}=\frac{1}{2\times \text{ }\frac{{{L}_{P}}}{{{R}_{P}}}~}=\frac{{{R}_{P}}}{2\times {{L}_{P}}}~ $$ (1) 式中：RL为数字鱼眼镜头的极限分辨率；RL为数字投影或放映机芯片的横向分辨率；LP为数字投影或放映机芯片的横向尺寸。
表 1列出了主流数字投影或放映机对数字鱼眼镜头极限分辨率的要求。一般情况下，镜头设计时会将极限分辨率的设计值提高到理论值的1.3到1.5倍，所以，实际数字鱼眼镜头的最高极限分辨率可能会达到100 lp/mm，甚至会更高。考虑到检测系统的通用型，鉴别率标板的单个分辨率图案包含5组线对，分别为125 lp/mm、100 lp/mm、80 lp/mm、63 lp/mm、50 lp/mm。鉴别率标板的尺寸根据各种规格的数字鱼眼镜头的成像像高而确定，每种规格的鉴别率标板在0、0.3、0.5、0.7、0.85视场上均匀分布着单个分辨率图案，如图 1所示，给出了鉴别率标板的示意图。
表 1 不同数字投影机对应的镜头极限分辨率Table 1. Different types of digital projectors and corresponding ultimate resolutions of lenses芯片尺寸/in 芯片像素 极限分辨率/lp/mm 0.76 1 920×1 200 59 0.7 1024×768 36 0.67 1 920×1 200 66.5 0.65 1 920×1 080、1 280×800、1 024×768 66.8 /45.7 /38.8 1.2 2 048×1 080 38 1.38 4 196×2 160 67 3.2 照明系统的设计
目前投影显示系统中主要采用复眼透镜照明系统和方棒照明系统2种照明方式[9]。
复眼透镜照明系统采用双排复眼透镜，属于柯拉照明。照明系统由于光源的整个光束被分为多个细光束照明，而且对称位置上的细光束光斑互相叠加，所以形成了较为均匀的照明场。但是复眼透镜照明系统结构较为复杂，很难保证2组复眼透镜严格的同轴，加工较为困难。
而方棒照明系统采用方棒形式，光在光棒里面多次反射，每次反射都会形成虚拟光源像，多次反射形成二维的虚拟光源矩阵，从而使得光更加均匀。但是方棒照明系统存在能量利用率相对较低，而且系统结构较长。
为了克服现有投影照明系统的不足和缺点，研究讨论了采用柱体(六边形)蝇眼透镜照明系统来提供高均匀的照明场。相比双排复眼透镜结构，柱体蝇眼透镜结构不但避免了在加工工艺中产生的两组蝇眼镜不同轴的误差和前后组蝇眼之间的粘合剂对光的吸收、散射以及杂光的入侵问题，而且还减少了加工面，简化了机械固定结构；相比方棒结构，能量利用率更高，系统的结构更加紧凑，有利于小型化。
系统由抛物型的反光碗光源、柱体蝇眼透镜阵列、准直物镜(场镜和集光镜)组成。其工作原理图如图 2所示，抛物型的反光碗光源发出类平行光，类平行光进入柱体蝇眼透镜阵列被形成多点光源，多点光源经准直物镜的调制之后均匀叠加在系统片窗上，如图 3所示。
3.3 照明系统中关键元件基本参数的确定
准直物镜的焦距f准与照明场的大小y存在以下关系：
$$ {f_{准}} = \frac{{y/2}}{{{\rm{tan}}w}} $$ (2) 式中，w为准直透镜的视场角，如图 4所示。
准直物镜的焦距f准与柱体蝇眼透镜组的子午方向上下边缘2个柱体中心距H(如图 3所示)的关系：
$$ H = {f_{准}}\cdot{\rm{tan}}\theta $$ (3) 式中，θ是准直物镜光学系统的孔径角。
该投影照明系统中柱体蝇眼透镜组的焦平面与准直物镜的物平面重合，即单个柱体透镜的像方孔径角也是准直物镜的视场角，故有：
$$ {f_{柱}} = \frac{{h/2}}{{{\rm{tan}}w}}{\rm{ }} $$ (4) 式中：f柱是单个柱体透镜的焦距；h是单个柱体透镜上下边的距离。
柱体蝇眼透镜组的子午方向上下边缘2个柱体中心距H与单个柱体透镜上下边的距离h之间的关系如下：
$$ ~H=h(n-1) $$ (5) 式中n为柱体蝇眼透镜组子午方向柱体透镜的总个数。
照明系统中，柱体透镜的排列方式，如图 3所示，故，柱体蝇眼透镜组的小透镜的总个数为
$$ N=1+\sum\limits_{1}^{\left( n-1 \right)/2}{\text{ }6\cdot \frac{\left( n-1 \right)}{2}}\text{ }~ $$ (6) 考虑到缩短整个光路，以及有效地提高照度均匀度，取准直透镜的视场角w=6°，准直物镜光学系统的孔径角θ=4°，再由各参数之间的关系式(2)~(6)，最终得出关键元件的设计尺寸。
3.4 照明视场大小可变功能的实现
测试系统需要满足不同类型数字鱼眼镜头的检测，故所需的照明视场大小也不同，为了防止光能量的不必要损失，测试系统应该具有照明视场大小可调的功能。由(2)式知，当系统的准直透镜的视场角确定后，改变准直透镜的焦距，就可以改变照明场的大小。通过改变场镜和集光镜之间的距离便可以得到不同焦距值的准直透镜[10]，进而实现照明视场的大小变化。
4 设计结果
设计了一款通用型数字鱼眼镜头检测系统，如图 4所示，主要由照明系统、检测标板、等效平行平板系统和球幕组成。照明系统采用的柱体蝇眼透镜阵列是由91个六边形柱透镜组成，测试标板主要是鉴别率板，用于检测数字鱼眼镜头的分辨率；等效平行平板系统是由4种不同厚度的平行平板组成，不同的组合可以满足不同类型数字鱼眼镜头的测试。球幕内部刻有角度线，用于检测数字鱼眼镜头的视场角。
经过定量化性能测试，主要性能指标测试结果如表 2所示，满足了设计指标要求。
表 2 检测系统测试结果Table 2. Testing result of testing system主要性能 测试结果 参数指标 照明视场范围φ/mm 8.1~36.3 ＞8.5~35 照度均匀度/% 91 ≥85 出射光通量/lm ≥5 000，可调 ≥5 000 5 结论
本文设计的通用型数字鱼眼镜头检测系统采用的柱体蝇眼透镜阵列照明系统不但光能利用率高，可产生较高的均匀度，而且有较高的准直性和较好的光束控制。通过调整更换不同厚度的等效平行玻璃平板，用于模拟各种数字投影或放映机内部棱镜，同时在片门处调换不同类型、不同尺寸的测试标板，被检测的数字鱼眼镜头将测试标板成像在球幕上，可实现对芯片尺寸为0.55″~1.55″的1DLP、3DLP、3LCD、3LCOS的各种类型的数字投影或放映鱼眼镜头的像方视场角、分辨率、彩色还原性能、色差等性能和放映效果进行测试，通用性强，降低了鱼眼镜头产品的检测成本。
-
![]()
图 8 空间域不同插值方法重聚焦效果
Figure 8. Refocusing effects of different interpolation methods in spatial domain
![]()
图 11 频域不同插值方法重聚焦效果
Figure 11. Refocusing effects of different interpolation methods in frequency domain
![]()
图 12 频域不同方法重聚焦效率
Figure 12. Refocusing efficiency of different methods in frequency domain
![]()
图 14 两种重聚焦方法的远近景重聚焦效果（左：近景；右：远景）
Figure 14. Far-and-close view refocusing effects of two refocusing methods（left：close view，right：far view）
表 1 空间域重聚焦图像质量指标值
Table 1 Index value of refocusing image quality in spatial domain
nearest linear cubic NIQE 15.808 16.015 15.778 BIQI 24.531 5.521 3.492 
下载: 导出CSV
表 2 频域重聚焦图像质量指标值
Table 2 Index value of refocusing image quality in frequency domain
nearest linear cubic sinc，R=1 sinc，R=2 sinc，R=3 PSNR 25.185 25.554 25.868 25.848 25.909 25.888 MSSIM 0.951 0.973 0.977 0.975 0.979 0.980
下载: 导出CSV
表 3 重聚焦图像质量指标值
Table 3 Index value of refocusing image quality
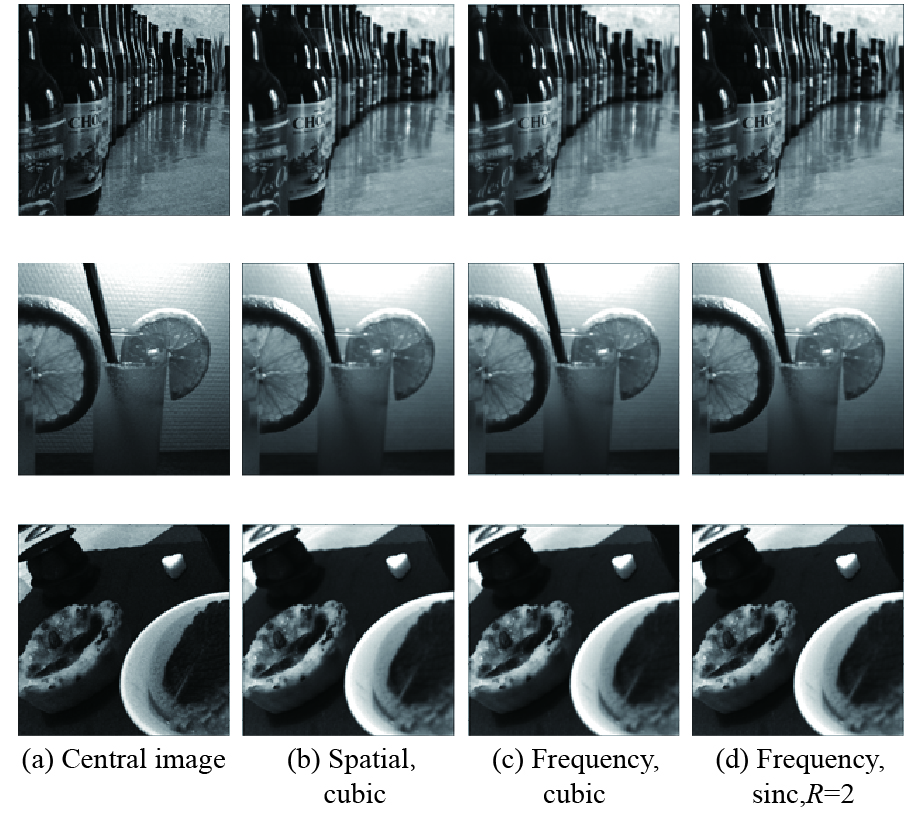
Method Spatial, cubic Frequency, cubic Frequency, sinc, R=2 beers BIQI 43.484 42.869 41.847 NIQE 16.187 16.611 16.212 cocktails BIQI 41.341 44.413 44.267 NIQE 18.283 18.411 18.308 dessert BIQI 44.752 41.752 41.699 NIQE 17.615 17.596 17.556
下载: 导出CSV
-
[1] GERSHUN A. The light field[J]. Journal of Mathematics and Physics,1939,18(1/2/3/4):541-151.
[2] ADELSON E H. The plenoptic function and the elements of early vision[M]//Computational Models of Visual Processing. [S.l]: The MIT Press, 1991.
[3] MCMILLAN L, BISHOP G. Plenoptic modeling[C]//Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques - SIGGRAPH '95. USA: ACM Press, 1995.
[4] LEVOY M, HANRAHAN P. Light field rendering[C]//Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques - SIGGRAPH '96. USA: ACM Press, 1996
[5] ADELSON E H, WANG J Y A. Single lens stereo with a plenoptic camera[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):99-106. doi: 10.1109/34.121783
[6] REN N. Digital light field photography[J]. Phd Thesis Stanford University,2006,115(3):38-39.
[7] LIM J G, BOUMAN C A, POLLAK I, et al. Computational Imaging VIII - Restoring the spatial resolution of refocus images on 4D light field[J]. SPIE,2010,7533:753310.
[8] 袁艳, 周宇, 胡煌华. 光场相机中微透镜阵列与探测器配准误差分析[J]. 光子学报,2010,39(1):123-126. doi: 10.3788/gzxb20103901.0123 YUAN Yan, ZHOU Yu, HU Huanghua. Registration error analysis for microlens array and photosonser in light field camera[J]. Acta Photonica Sinica,2010,39(1):123-126. doi: 10.3788/gzxb20103901.0123
[9] 张旭, 李晨. 微透镜阵列式光场成像模型及其标定方法[J]. 光学学报,2014,34(12):95-107. ZHANG Xu, LI Chen. Calibration and imaging model of light field camera with microlens array[J]. Acta Optica Sinica,2014,34(12):95-107.
[10] LEVOY M, ZHANG Z, MCDOWALL I. Recording and controlling the 4D light field in a microscope using microlens arrays[J]. Journal of Microscopy,2009,235(2):144-162. doi: 10.1111/j.1365-2818.2009.03195.x
[11] 杨凡, 袁艳, 周志良. 光场相机成像质量评价方法研究[J]. 现代电子技术,2011,34(6):4-6. doi: 10.3969/j.issn.1004-373X.2011.06.002 YANG Fan, YUAN Yan, ZHOU Zhiliang. Study on imaging quality evaluation of light field camera[J]. Modern Electronics Technique,2011,34(6):4-6. doi: 10.3969/j.issn.1004-373X.2011.06.002
[12] HUANG C T. Fast realistic refocusing for sparse light fields[C]//IEEE International Conference on Acoustics. USA: IEEE, 2015.
[13] WANNER S, GOLDLUECKE B. Variational light field analysis for disparity estimation and super-resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2014,36(3):606-619. doi: 10.1109/TPAMI.2013.147
[14] HORSTMEYER R, EULISS G, ATHALE R. Flexible multimodal camera using a light field architecture: 2009 IEEE International Conference on Computational Photography (ICCP), San Francisco, CA, April 16-17, 2009[C]. USA. IEEE, 2009.
[15] PÉREZ F, PÉREZ A, RODRÍGUEZ M, et al. Super-resolved Fourier-slice refocusing in plenoptic cameras[J]. Journal of Mathematical Imaging and Vision,2015,52(2):200-217. doi: 10.1007/s10851-014-0540-1
[16] GEORGIEV T, YU Z, LUMSDAINE A, et al. Lytro camera technology: theory, algorithms, performance analysis[C]//Proceedings of SPIE - The International Society for Optical Engineering. [S.l]: SPIE, 2013: 8667.
[17] MOORTHY A K, BOVIK A C. A two-step framework for constructing blind image quality indices[J]. IEEE Signal Processing Letters,2010,17(5):513-516. doi: 10.1109/LSP.2010.2043888
[18] MITTAL A, SOUNDARARAJAN R, BOVIK A C. Making a “completely blind” image quality analyzer[J]. IEEE Signal Processing Letters,2013,20(3):209-212. doi: 10.1109/LSP.2012.2227726
[19] NG Ren. Fourier slice photography[J]. ACM Transactions on Graphics,2005,24(3),735-744.
[20] MAYMON S, OPPENHEIM A V. Sinc interpolation of nonuniform samples[J]. IEEE Transactions on Signal Processing,2011,59(10):4745-4758. doi: 10.1109/TSP.2011.2160054
-
期刊类型引用(1)
1. 路文文，陈善勇，翟德德，熊玉朋. 混合仿生鱼眼-复眼的广角高清成像系统. 应用光学. 2019(02): 311-315 . 
本站查看
其他类型引用(1)
计量
- 文章访问数: 1780
- HTML全文浏览量: 538
- PDF下载量: 53
- 被引次数: 2
陕公网安备 61011302001501号 